BFS(Breadth First Search)
너비를 우선으로 탐색을 수행하는 알고리즘
맹목적인 탐색을 할 때 사용하는 기법
"최단 경로"를 찾아준다는 점에서 최단 길이를 보장해야 할 때 많이 사용함
ex) 지구 상에 존재하는 모든 친구 관계를 그래프로 표현한 후 Ash와 Vanessa 사이에 존재하는 경로를 찾는 경우
DFS - 모든 친구 관계를 다 살펴 봐야 함
BFS - Ash와 가까운 관계부터 탐색
필요한 자료구조는 Queue (FIFO : 선입선출의 원칙)
<특징>
- 직관적이지 않음 (시작 노드에서 거리에 따라 단계별 탐색)
- 재귀적이지 않음
- 어떤 노드를 방문했었는지를 반드시 검사해야 무한루프에 빠질 위험이 없다
- Prim, Dijkstra 알고리즘과 유사하다
<장점>
- 노드의 수가 적고 깊이가 얕은 경우 빠르게 동작
- 단순 검색 속도가 DFS 보다 빠름
- 최단 경로임을 보장
- 최단 경로가 존재한다면 반드시 최단 경로를 찾을 수 있다
<단점>
- 재귀호출을 하는 DFS와는 달리 queue에 다음 탐색을 위한 정점들을 저장해야 하므로 저장공간이 많이 필요
- 노드의 수가 늘어나면 탐색해야하는 노드가 많아진다
<BFS 탐색 과정>
깊이가 1인 모든 노드 방문 후 깊이의 오름차순으로 방문하다가 더 이상 방문할 노드가 없다면 탐색을 종료한다
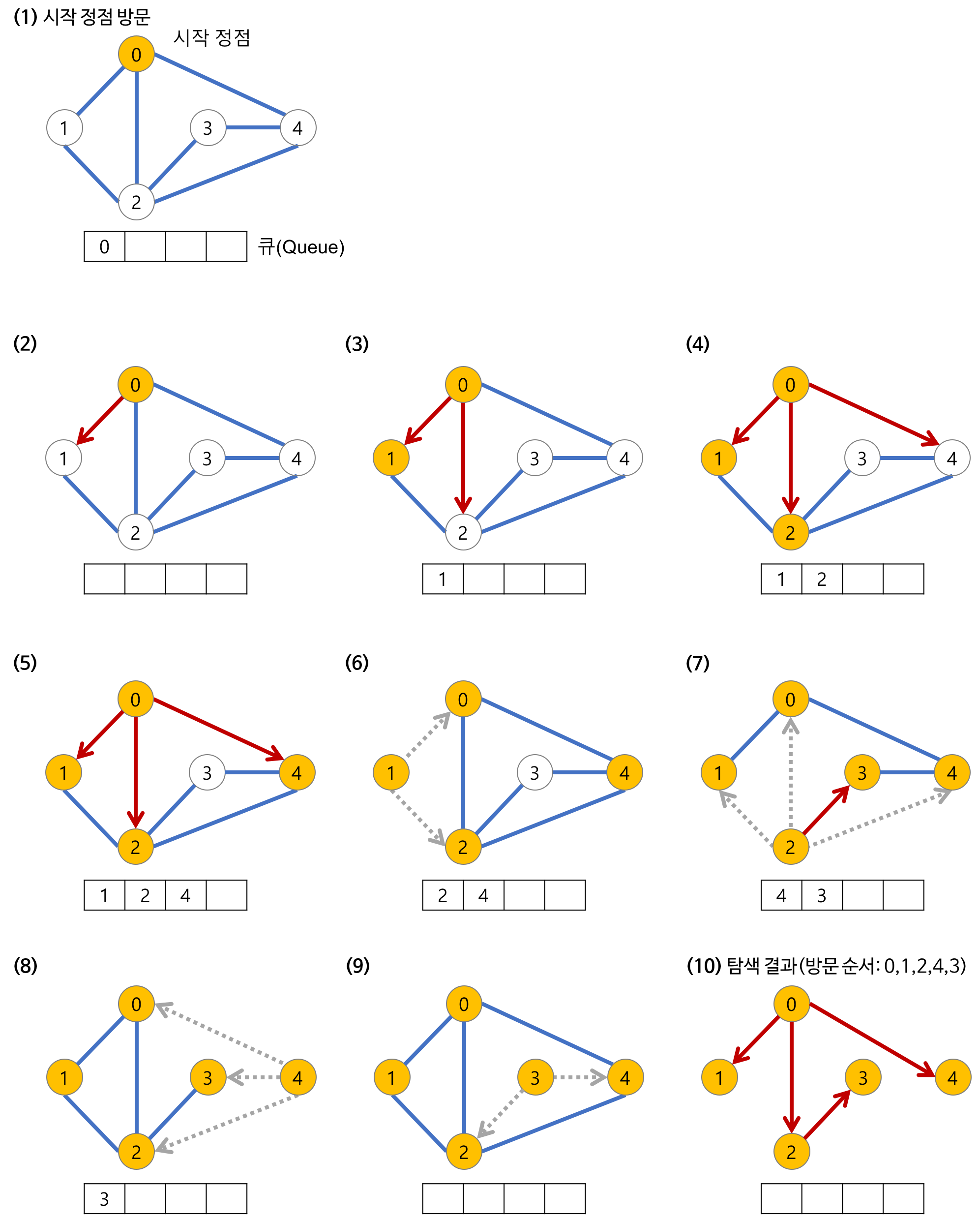
<코드>
사용 언어 : c++
#include <iostream>
#include <queue>
#include <vector>
using namespace std;
int number = 7;
int check[5]; // 방문 처리를 위한 배열
vector<int> a[5]; // 각 노드의 인덱스가 1부터 처리될 수 있도록 만든 배열
void bfs(int start) {
queue<int> q;
q.push(start); // 시작 노드
check[start] = true; // 방문 처리
while (!q.empty()) { // queue가 비어있지 않다면(탐색 중)
int x = q.front(); // queue의 맨 처음 원소를 x에 넣고
q.pop(); // 빼낸다
cout << x << " ";
for (int i = 0; i < a[x].size(); i++) { // queue에서 꺼낸 인접한 노드를 방문하면서
int y = a[x][i]; // 방문을 하면서
if (!check[y]) { // 방문 한 상태가 아니라면
q.push(y); // queue에 노드를 넣어주고
check[y] = true; // 방문 처리를 해준다
}
}
}
}
int main() {
a[0].push_back(1);
a[1].push_back(0);
a[0].push_back(2);
a[2].push_back(0);
a[0].push_back(4);
a[4].push_back(0);
a[1].push_back(2);
a[2].push_back(1);
a[2].push_back(3);
a[3].push_back(2);
a[2].push_back(4);
a[4].push_back(2);
a[3].push_back(4);
a[4].push_back(3);
bfs(0);
return 0;
}<BFS의 시간 복잡도>
인접 리스트로 표현된 그래프 : O(N+E)
인접 행렬로 표현된 그래프 : O(N^2)
그래프 내에 적은 숫자의 간선만을 가지는 희소 그래프의 경우 인접 행렬보다 인접 리스트를 사용하는 것이 유리
인접 행렬 vs 인접 리스트
인접 행렬 : 2차원 배열
인접 리스트 : 링크드 리스트, 어레이 리스트, 어레이 리스트를 저장하는 어레이 리스트