Dijkstra
다이나믹 프로그래밍을 활용한 대표적인 최단 경로 알고리즘
하나의 정점에서 다른 모든 정점까지의 최단 경로를 구할 때 사용한다
<특징>
- 하나의 최단 거리를 구할 때 그 이전까지 구했던 최단 거리 정보를 그대로 사용한다
- 음의 간선을 포함할 수 없어 현실 세계에 사용하기 매우 적합한 알고리즘
- 정렬을 사용하고 정렬 이후 가장 작은 것을 선택하므로 greedy 알고리즘으로 구분되기도 한다
<Dijkstra 동작 과정>
- 출발 노드 설정
- 출발 노드를 기준으로 각 노드의 최소 비용 저장
- 방문하지 않은 노드 중에서 가장 비용이 적게 드는 노드 선택
- 해당 노드를 거쳐 특정한 노드로 가는 경우를 고려하여 최소 비용 갱신
- 3, 4번 반복
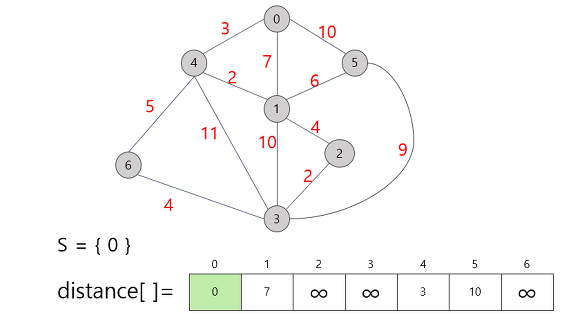
가장 짧은 거리는 정점 4까지의 거리인 3이므로 정점 4를 집합 S에 추가시킨다
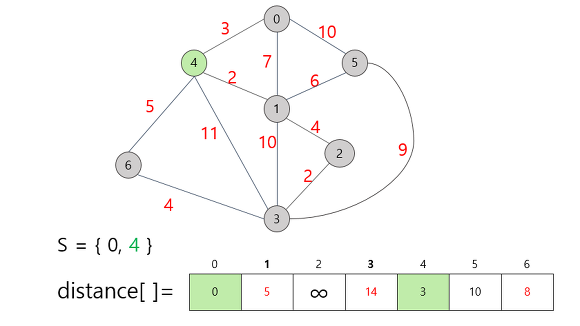
4번 정점을 택함으로써 1번 정점까지의 거리가 7이였던 것이 5로 줄어들었다. 갱신된 정보들을 바탕으로 집합 S에 추가할 다음 정점을 선택해보면 남은 정점 중 가중치가 가장 적게 표시되어 있는 건 정점 1이다. 1번 정점을 집합 S에 추가한 뒤 갱신 가능한 정보가 있으면 갱신해준다
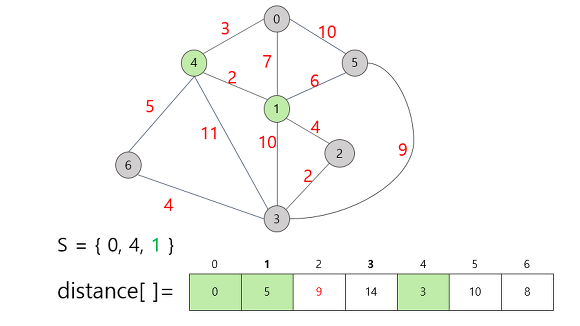
1번 정점을 추가함으로써 2번 정점까지 직접 갈 수 있게 되었으므로 무한대의 값에서 구체적인 가중치인 9로 수정해준다. 다음으로 가장 작은 값은 6번 정점의 8 이므로, 6번 정점을 택한 뒤 갱신 가능한 값을 갱신해준다
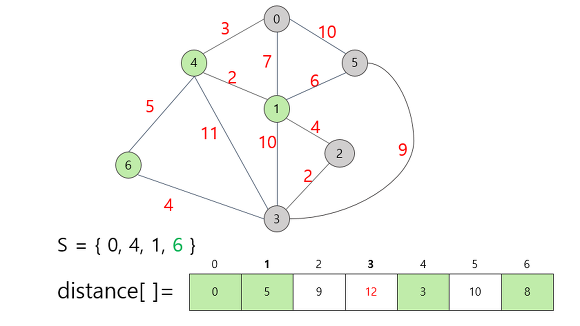
6번 정점을 집합 S에 추가함으로써 갱신할 수 있는 정보는 정점 3까지의 거리다. 기존의 14에서 12로 거리가 단축되었으므로 이 값을 갱신한다.
이제 방문하지 않은 정점 중 가장 작은 가중치 값을 가지는 정점인 2를 선택한다
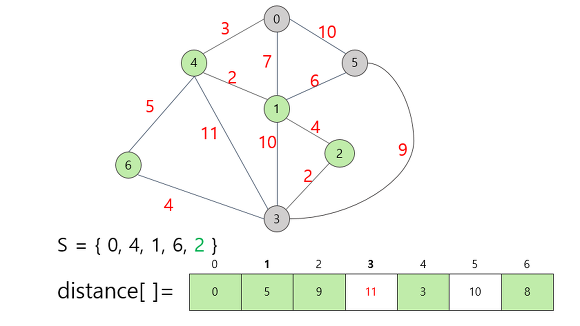
정점 2를 집합 S에 추가함으로써 정점 3까지의 거리가 갱신되고 이후 5번 정점 -> 3번 정점 순으로 택해준다
출처
<코드>
사용 언어 : c++ (선형 탐색을 이용)
#include <iostream>
using namespace std;
int number = 6; // 정점의 개수
int INF = 1000000000; // 무한대를 표현
// 전체 그래프를 초기화
// 특정한 행에서 열로 가는 비용
int a[6][6] = {
{0, 2, 5, 1, INF, INF},
{2, 0, 3, 2, INF, INF},
{5, 3, 0, 3, 1, 5},
{1, 2, 3, 0, 1, INF},
{INF, INF, 1, 1, 0, 2},
{INF, INF, 5, INF, 2, 0},
};
bool v[6]; // 방문을 한 노드인지 체크하기 위한 배열
int d[6]; // 최단 거리를 저장할 수 있도록 하는 배열
// 가장 최소 거리를 가지는 정점을 반환한다
int getSmallIndex() {
int min = INF;
int index = 0;
for (int i = 0; i < number; i++) {
if (d[i] < min && !v[i]) { // 방문하지 않은 노드 중에서
min = d[i]; // 현재 최소값보다 더 작은 값을 가지는 거리가 존재한다면
index = i; // 그 값으로 갱신해주고 그 때의 위치를 기억할 수 있도록 해준다
}
}
return index;
}
// 다익스트라를 수행하는 함수
void dijkstra(int start) { // 특정한 정점에서부터 다른 모든 정점으로 가는 최소 비용을 구함
for (int i = 0; i < number; i++) {
d[i] = a[start][i]; // 시작점으로부터 출발을 했을 때 각 정점까지의 모든 비용을 담아준다
}
v[start] = true; // 방문 처리
for (int i = 0; i < number - 2; i++) {
int current = getSmallIndex(); // 현재 방문하지 않은 노드 중에서 가장 빠르게 도착할 수 있는
v[current] = true; // 즉 최소비용을 가지는 노드의 인덱스를 가져와서 방문처리 해준다
for (int j = 0; j < 6; j++) { // 그 노드의 인접한 모든 노드를 탐색하면서
if (!v[j]) { // 그 노드를 방문하지 않았다면
if (d[current] + a[current][j] < d[j]) { // 현재 보고 있는 그 노드까지의 최소 비용에서
d[j] = d[current] + a[current][j]; // 그 노드를 거쳐서 그 노드의 인접한 노드까지 가는 비용을 더한 값이
} // 현재 그 인접한 노드로 가는 최소 비용보다 더 작다면 갱신해주면 된다
}
}
}
}
int main() {
dijkstra(0);
for (int i = 0; i < number; i++) { // 노드 1에서부터 모든 노드까지의 최단 거리를 구해본다
cout << d[i] << " ";
}
}위의 코드로 구현하게 되면 getSamllIndex()를 구하는 과정에서 n번의 반복이 생기고 dijkstra()에서 또 다시 n번의 반복이 생기므로 전체적인 시간복잡도는 O(n^2)이 되어 정점의 개수는 많지만 간선은 적을 때 아주 비효율적이게 된다
★ 이를 Heap을 사용하여 개선시킬 수 있는데
Heap은 항상 가장 큰 값 혹은 작은 값이 최상단 노드에 존재한다는 특징이 있으므로 가장 작은 값을 가져오는 시간복잡도를 logn 으로 줄일 수 있다 따라서 전체 시간복잡도는 O(nlogn)이 된다
<코드>
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
int number = 6;
int INF = 100000000;
vector<pair<int,int>> a[7]; // 간선 정보
int d[7]; // 최소 비용
void dijkstra(int start) {
d[start] = 0;
priority_queue<pair<int, int> > pq; // 힙 구조 (최대힙)
pq.push(make_pair(start, 0)); // 가까운 순서대로 처리하므로 큐를 사용
while (!pq.empty()) { // queue가 비어있지 않다면 하나씩 꺼내면서
int current = pq.top().first; // 현재 방문하고자하는 노드가 큐의 최상단 노드에 있는 첫번째 값이 되도록 만들어준다
// 큐의 가장 위에는 가장 적은 비용을 가지는 노드의 정보가 있으므로
int distance = -pq.top().second;
// priority_queue는 최대힙 (가장 큰 값이 최상단 노드로 간다)
// 더 작은 값이 상단노드로 가도록 만들고 싶기 때문에 짧은 것이 먼저오도록 음수화해준다
// 거리 값에 - 를 붙여준다
// 최소 비용이 가장 적은 노드가 실질적으로 가장 큰 값으로 큐에 들어가도록 만들어지기 때문에
// 현재 최상단노드에 가장 비용이 적은 노드가 담겨져 있다는 것이다
pq.pop();
if (d[current] < distance) continue; // 최단 거리가 아닌 경우 스킵
for (int i = 0; i < a[current].size(); i++) {
// 선택된 노드의 인접 노드를 next에 담아주고
int next = a[current][i].first;
// 선택된 노드를 인접 노드로 거쳐서 가는 비용을 계산한다
int nextDistance = distance + a[current][i].second;
// 기존의 최소 비용보다 더 저렴하다면 교체
if (nextDistance < d[next]) {
d[next] = nextDistance;
pq.push(make_pair(next, -nextDistance));
// priority queue같은 경우에는
// 더 큰 값이 위쪽으로 가기때문에 우리가 원하는 더 작은 값이 위쪽으로 가게하려면 -를 붙여야 함
}
}
}
}
int main(void) {
for (int i = 1; i <= number; i++) { // 연결되지 않았다면 무한
d[i] = INF;
}
a[1].push_back(make_pair(2, 2));
a[1].push_back(make_pair(3, 5));
a[1].push_back(make_pair(4, 1));
a[2].push_back(make_pair(1, 2));
a[2].push_back(make_pair(3, 3));
a[2].push_back(make_pair(4, 2));
a[3].push_back(make_pair(1, 5));
a[3].push_back(make_pair(2, 3));
a[3].push_back(make_pair(4, 3));
a[3].push_back(make_pair(5, 1));
a[3].push_back(make_pair(6, 5));
a[4].push_back(make_pair(1, 1));
a[4].push_back(make_pair(2, 2));
a[4].push_back(make_pair(3, 3));
a[4].push_back(make_pair(5, 1));
a[5].push_back(make_pair(3, 1));
a[5].push_back(make_pair(4, 1));
a[5].push_back(make_pair(6, 2));
a[6].push_back(make_pair(3, 5));
a[6].push_back(make_pair(5, 2));
dijkstra(1);
for (int i = 1; i <= number; i++) {
cout << d[i] << " ";
}
}이렇게 인접 리스트를 활용하면 시간복잡도를 O(n*logn)으로 줄일 수 있고 정점에 비해 간선의 개수가 비정상적으로 적어도 안정적인 처리가 가능하게 된다