[정수론] 에라토스테네스의 체

📌 에라토스테네스의 체

⭐ 개념

• 소수 판별 알고리즘
• 소수가 되는 수의 배수를 지우면 남은 건 소수가 된다

✅ 시간복잡도

• O(Nlog(logN))

⭐ 실행과정

1. 구하고자 하는 소수의 범위만큼 1차원 배열을 생성
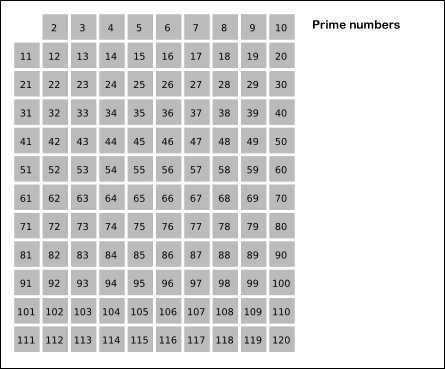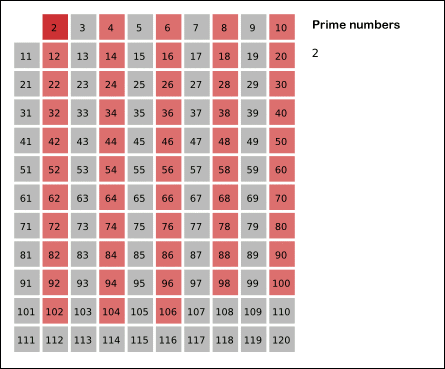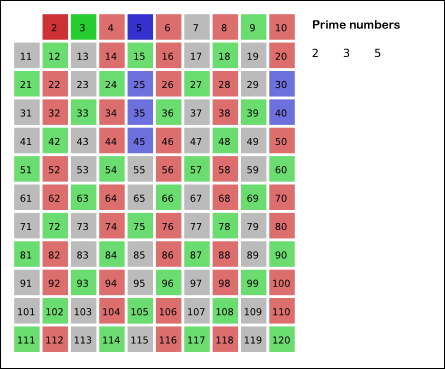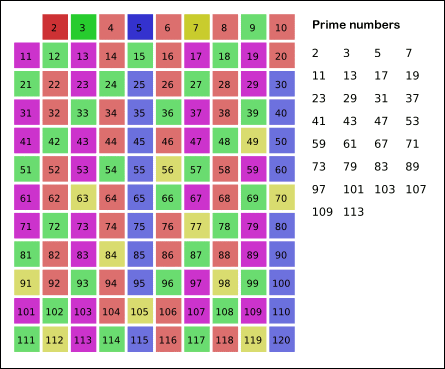
2. 2부터 시작해서 현재 선택된 숫자의 배수에 해당하는 수를 배열끝까지 탐색하면서 지움(보통 0으로 바꿈)
3. N의 제곱근만큼 반복한 뒤 결과적으로 남아있는 것이 소수

✅ 제곱근까지만 수행하는 이유?

ex) 가령 64라는 수를 가정해보자. 실제로 64는 소수가 아니다. 64를 구성하는 약수의 구성을 살펴보면 1x64 , 2x32 , 4x16, 8x8 => 1,2,4,8,16,32,64
위의 형태로 약수가 구성되어 있다.
즉 n의 제곱근을 중심으로 더 작은수 X 더 큰 수로 만들어진게 n이라는 숫자인 것이다.
따라서 n의 제곱근보다 작은 수 중에서 약수가 없다면 제곱근 중에서 더 큰수 두개끼리 N의 약수가 될 수 없는 것이다

⭐ 코드

public class Main {
  public static void main(String[] args) {
  	int N = 100; // 100이하의 소수 구하기
    int[] A = new int[N + 1];
    
    // 배열 초기화
    for (int i = 2; i <= N; i++) {
      A[i] = i;
    }
    for (int i = 2; i <= Math.sqrt(N); i++) { // 제곱근 까지만 수행
      if (A[i] == 0) {
        continue;
      }
      for (int j = i + i; j <= N; j = j + i) { // 배수 지우기
        A[j] = 0;
      }
    }
    // 소수 출력
    for (int i = 2; i <= N; i++) {
      if (A[i] != 0) {
        System.out.println(A[(int) i]);
      }
    }
  }
}