[정수론] 오일러 파이

📌 오일러 파이(피)

⭐ 개념

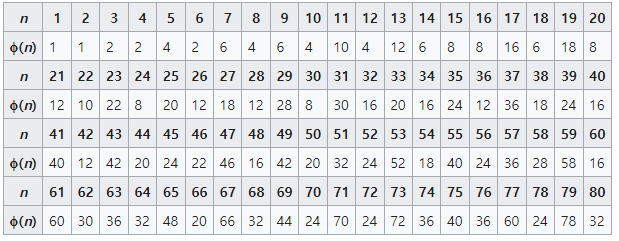
• φ[N]의 정의는 1부터 N까지 범위에서 N과 서로소인 자연수의 개수
  ex) φ[6] : 2(1, 5) => 6과 서로소인 수의 개수(1 ~ 6 범위 안에서)
• 오일러 파이 함수의 원리는 에라토스테네스의 체를 활용함
• GCD(n,k) = 1과 같은 의미(두 수의 최대공약수가 1)

✅ 서로소

• 공약수가 1 이외에 X

⭐ 실행과정

1. 구하고자 하는 오일러 피의 범위만큼 배열을 자기 자신의 인덱스값으로 초기화
2. 2부터 시작해 현재 배열의 값과 인덱스가 같으면(=소수일때) 현재 선택된 숫자(K)의 배수에 해당하는 수를 배열 끝까지 탐색하여 φ[i] = φ[i] - φ[i]/K 연산을 수행한다.(i는 K의 배수)
3. 배열의 끝까지 2를 반복하여 오일러 피 함수를 완성한다

✅ 수학적 이해

• 초기상태 : φ(6) = 6 -> 서로소가 될 수 있는 후보개수 초기화(1,2,3,4,5,6)
• 2의 배수로 인한 탈락 -> φ(6) = 6 - (6/2) = 3(1,3,5)
• 3의 배수로 인한 탈락 -> φ(6) = 3 - (3/3) = 2(1,5)
  • 이때 후보에서 삭제하는 기준을 6이 아닌 업데이트 된 3으로 진행하는 이유는 3의 배수이자 2의 배수인 6이 이미 2의배수에서 탈락했기 때문이다.

✅ 핵심 포인트

1. 소인수는 항상 제곱근보다 작은 수가 1개 아니면 0개이다.
   ex) 10 = 2 * 5인데 10의 제곱근은 3.xx이므로 큰 값은 5 1개다.
   => 이를 통해, 제곱근보다 큰값은 마지막에 한번 처리해준다.
2. 소인수를 완전 없애는 과정이 필요하다.
   ex) 20 = 2의 제곱 * 5인데 나누기를 통해 2를 소인수에서 아예없애준다.
3. 마지막에 n이 1이면 소인수가 해당수의 제곱근보다 다 작은값이었기에 for문에서 다 처리된거고, n보다 크다면 제곱근보다 큰 값이 1개가 남아있는 것이기에 오일러 파이 함수를 한번 더 해준다.

⭐ 코드

// 오일러 파이 전체 배열을 구하는 것이 아닌 특정값에 대해 구하는 코드
import java.io.*;
public class Main {
  public static void main(String[] args) throws Exception {
    BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
    long n = Long.parseLong(br.readLine());
    long result = n;
    for (long p = 2; p <= Math.sqrt(n); p++) { // 제곱근까지만 진행
      if (n % p == 0) { // p가 소인수인지 확인
        result = result - result / p; // 오일러 피 함수
        while (n % p == 0) { // 해당 소인수를 지워줌 2^7*11이라면 2^7을 없애고 11만 남김
          n /= p;
        }
      }
    }
    if (n > 1) 
    // 아직 소인수 구성이 남아있는 경우
	//(반복문에서 제곱근까지만 탐색했기 때문에 1개의 소인수가 누락되는 케이스)
      result = result - result / n;
    System.out.println(result);
  }
}