[JS] Leetcode.587 Erect The Fence

황준승·2021년 9월 4일

문제 링크 : https://leetcode.com/problems/erect-the-fence/

이 문제는 Convew Hull(볼록 껍질) 알고리즘으로 대표적으로 세가지 방법이 존재합니다.

1. Jarvis Algorithm
2. Graham Scan
3. MonotoChain

그 중 저는 MonotoChain 방법을 사용하였습니다.

Convew Hull(볼록 껍질 알고리즘)

정의
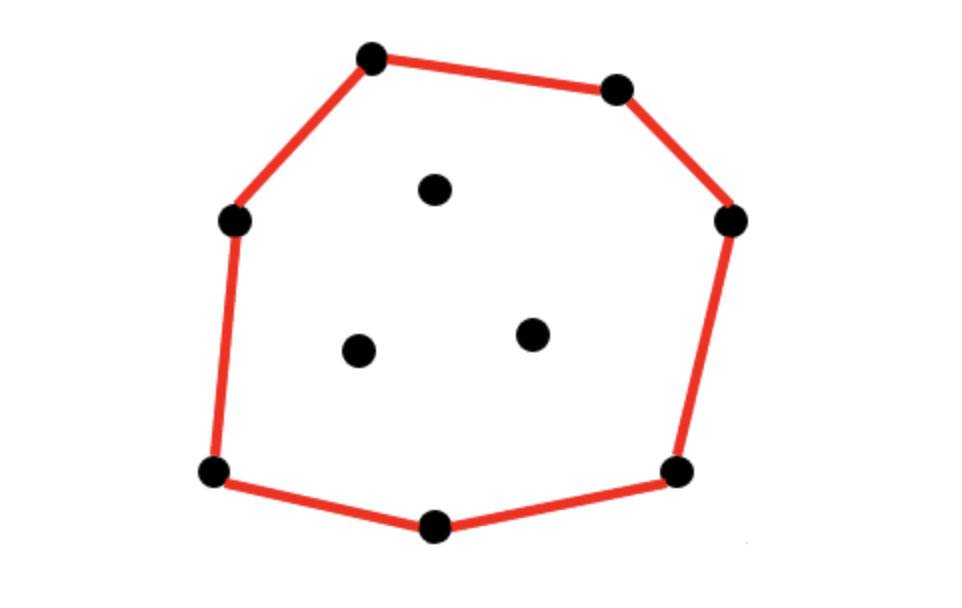
"2차원 평면 상에서 주어진 점들을 모두 포함하는 가장 작은 다각형"

이게 뜻이 모호할 수 있으니 정의를 확실히 잡고 가도록 하겠습니다. 사실 선을 어떻게 그어도 점을 다 포함할 수 있는 방법은 굉장히 많습니다.

예)

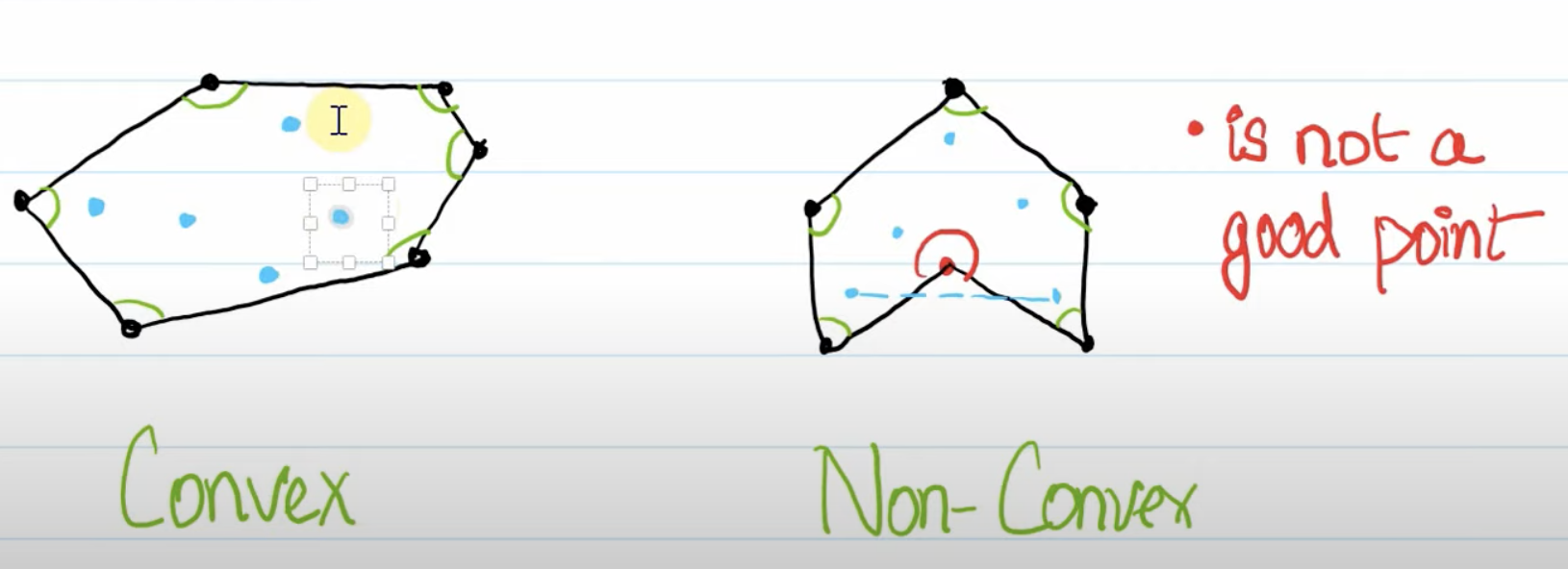
여기서 오른쪽 그림을 살펴보자.

모든 점들이 선 안에 들어가긴 하였지만 이는 최소 선의 개수로 이어진 것이 아니다. 만약에 오른쪽 도형이 5각형 형태의 모형이 되어 있다면 최소 선의 개수로 볼록 껍질을 완성할 수 있을 것이다.

그렇다면 왼쪽 그림을 보도록 하자.

위의 그림과 왼쪽 그림을 보면서 볼록 껍질의 특징을 하나 알 수 있다. 이는 시계 모양과 같은 원 모양에 가깝다라는 것을 알 수 있다. (모든 점을 포획하려다 보니 동글동글한 모양을 가지고 있는 거 같음)

CCW 알고리즘

정의

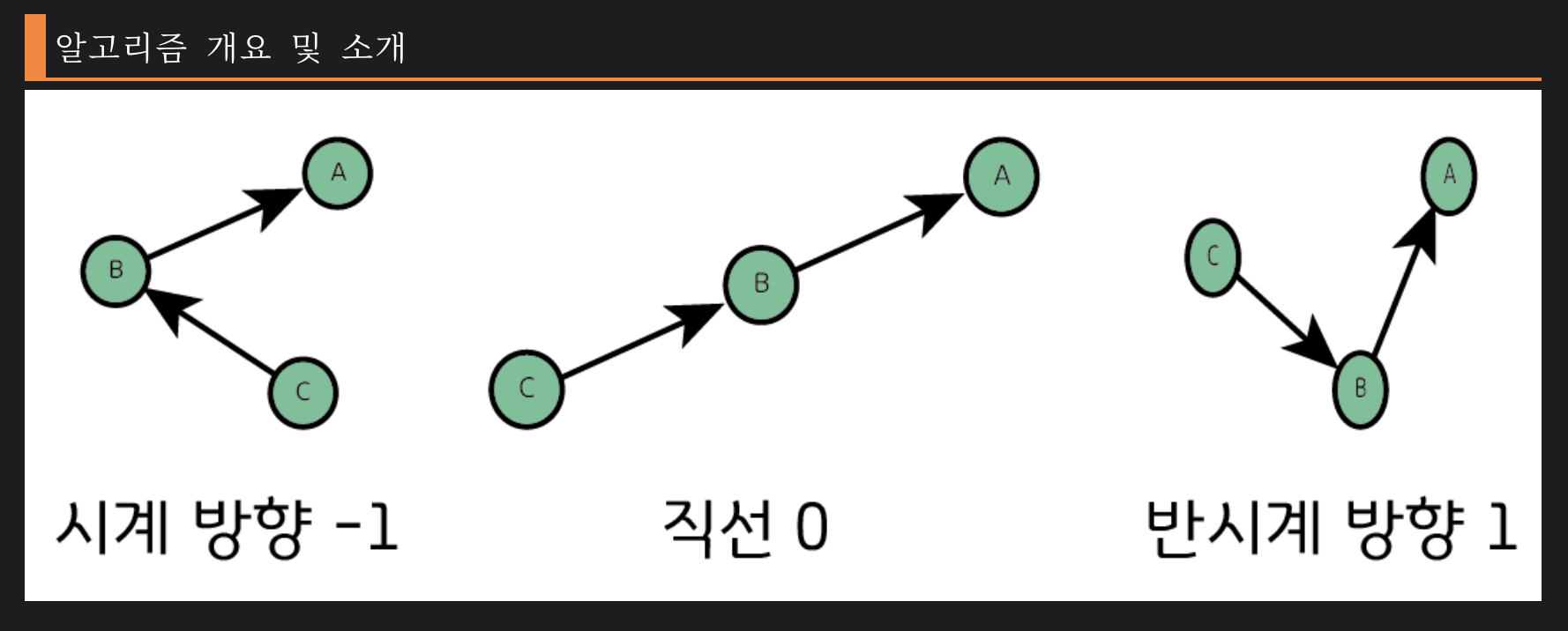
CCW( Counter Clock Wise) 알고리즘은 3개의 점 A, B, C가 있을 때 이 점 3개를 이은 직선의 방향을 알고자 할 때 유용한 기하 알고리즘이다.

경우의 수는 총 3가지가 있으며 시계, 반시계, 직선이 있으며 이는 외적 을 통하여 구할 수 있으며 외적의 결과가 음수이면 시계 방향, 직선은 0, 반시계 방향일 경우 양수가 나오게 된다. (아래 그림 참조)

CCW 구하는 방법

예시 : p1p2를 이은 선분벡터, p2p3를 이은 선분벡터의 CCW를 구하기
p1 = (x1,y1)
p2 = (x2,y2)
p3 = (x3,y3)

solution

p1p2를 이은 선분벡터, p2p3를 이은 선분벡터의 외적을 구한 다음 해당 값의 결과값(음수, 양수, 0)에 따라 시계, 반시계, 직선인지 결정한다.

외적 공식

|(x2 - x1) (y2 - y1)|
|(x3 - x2) (y3 - y2)|

즉, (y3 - y2)*(x2 - x1) - (x3-x2) * (y2-y1)

이를 코드화 하면 다음과 같다.

/**
 * 
 * @param {number[][]} p1 
 * @param {number[][]} p2 
 * @param {number[][]} p3 
 * @returns {number}
 */
function ccw(p1, p2, p3){
    return (p3[1] - p2[1])*(p2[0]-p1[0]) - (p2[1]-p1[1])*(p3[0]-p2[0]);
}

Monotone Chain 알고리즘

위의 gif파일에서 볼 수 있듯이 세 개의 점들의 ccw 알고리즘 결과를 비교하여 일정한 방향으로 돌지 않으면 해당 점을 포함하지 않는 알고리즘이다.

코드 구현 설명

Monotone Chain 알고리즘을 사용하지만 좀 더 쉬운 구현을 위해 위의 gif 파일과는 약간은 다른 방식을 사용하였다. 앞서 볼록 껍질은 원에 가까운 형태를 띈다고 했다. 그렇다면 시작점을 기준으로 아래 그림과 같은 형식이 무조건 만들어 지지 않을까라는 생각을 해보았다.

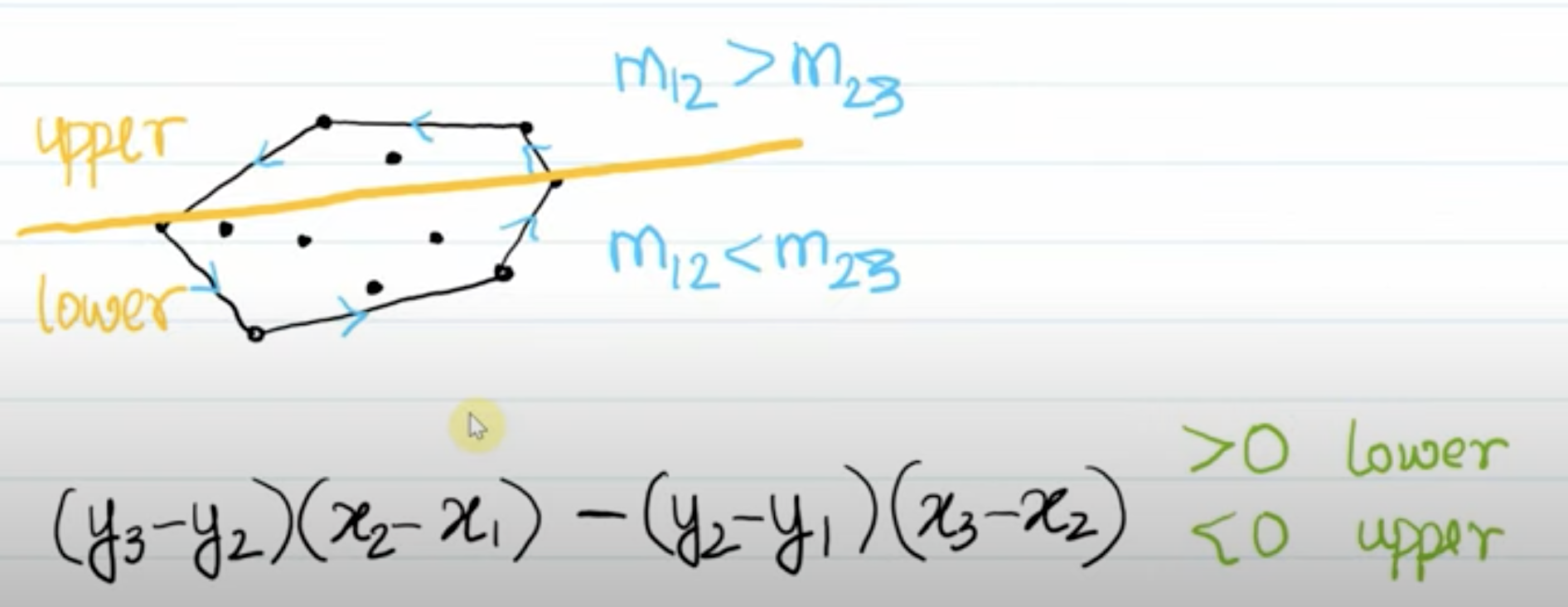
tip : 정렬된 배열에서 배열의 제일 첫번째 점을 기준으로 점들을 비교하기 때문에 시계 방향과 반시계 방향을 모두 체크해주어야 볼록껍질의 모든 점들을 가져올 수 있다.

tip 구현

    for (let t of trees){
        // upper는 반시계 방향일 때만 가져온다. -> 시계방향( ccw < 0 )일 경우 pop()
        while (upper.length >= 2 && ccw(upper[upper.length - 2], upper[upper.length-1], t) < 0){
            upper.pop();
        }
        // lower는 시계 방향일 때만 가져 온다. => 반시걔 방향 ( ccw > 0) 일 경우 pop()
        while (lower.length >= 2 && ccw(lower[lower.length -2], lower[lower.length-1], t) > 0){
            lower.pop();
        }
        upper.push(t);
        lower.push(t);
    }
    return [...new Set([...upper,...lower])];
};

전체 코드

// leetcode 587 ErectTheFence

// Input: points = [[1,1],[2,2],[2,0],[2,4],[3,3],[4,2]]
// Output: [[1,1],[2,0],[3,3],[2,4],[4,2]]

/**
 * 
 * @param {number[][]} p1 
 * @param {number[][]} p2 
 * @param {number[][]} p3 
 * @returns {number}
 */
// ccw 알고리즘 함수
function ccw(p1, p2, p3){
    // 외적을 구하는 함수 - 외적을 통해 해당 선분이 어떤 방향으로 돌아가고 있는지 판단
    // 음수 : 시계 방향
    // 0 : 직성
    // 양수 : 반시계 방향
    return (p3[1] - p2[1])*(p2[0]-p1[0]) - (p2[1]-p1[1])*(p3[0]-p2[0]);
}

/**
 * @param {number[][]} trees
 * @return {number[][]}
 */
const outerTrees = function(trees) {
    
    // 정렬
    trees.sort((a,b) => (a[0] - b[0]) || (a[1] - b[1]));
    
    let upper = [];
    let lower = [];

    for (let t of trees){
        // upper는 반시계 방향일 때만 가져온다. -> 시계방향( ccw < 0 )일 경우 pop()
        while (upper.length >= 2 && ccw(upper[upper.length - 2], upper[upper.length-1], t) < 0){
            upper.pop();
        }
        // lower는 시계 방향일 때만 가져 온다. => 반시걔 방향 ( ccw > 0) 일 경우 pop()
        while (lower.length >= 2 && ccw(lower[lower.length -2], lower[lower.length-1], t) > 0){
            lower.pop();
        }
        upper.push(t);
        lower.push(t);
    }
    return [...new Set([...upper,...lower])];
};