머신러닝을 활용할 때 올바른 평가 지표를 사용하는 것은 2가지 측면에서 정말 중요합니다.
- 해결하려는 문제에 적합한 평가 지표를 활용해야 한다.
- 다른 부서와 커뮤니케이션을 고려한 평가 지표를 사용해야 한다.
머신러닝 회귀 모형에서 적절한 평가 지표를 사용하기 위해 아래의 총 5가지의 지표의 특징에 대해서 정리해보려고 합니다.
MAE: Mean Absolute ErrorMSE: Mean Square ErrorRMSE: Root Mean Square ErrorMAPE: Mean Absolute Percentage ErrorMPE: Mean Percentage Error
1. MAE
- 공식: 잔차의 절댓값에 대한 평균
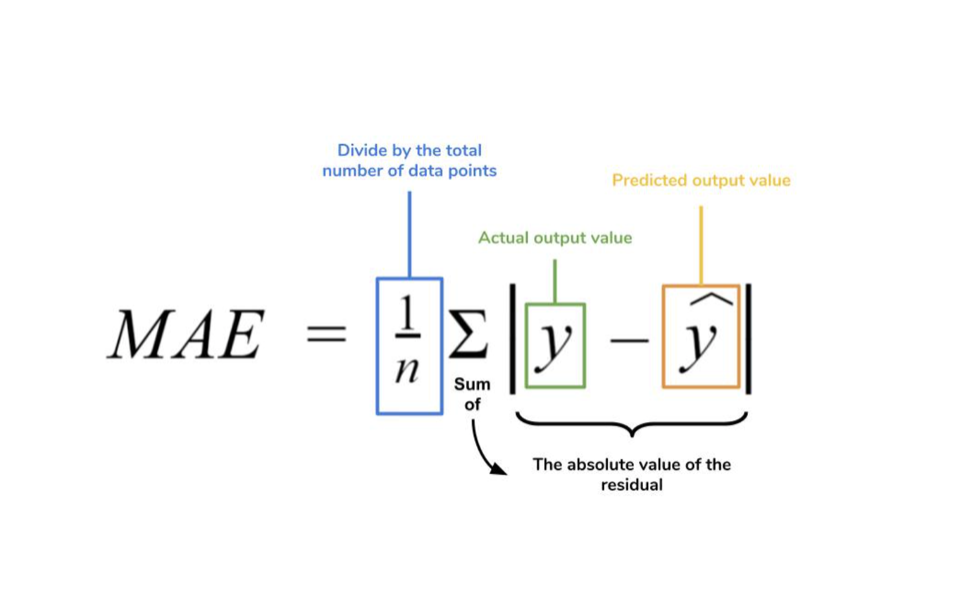
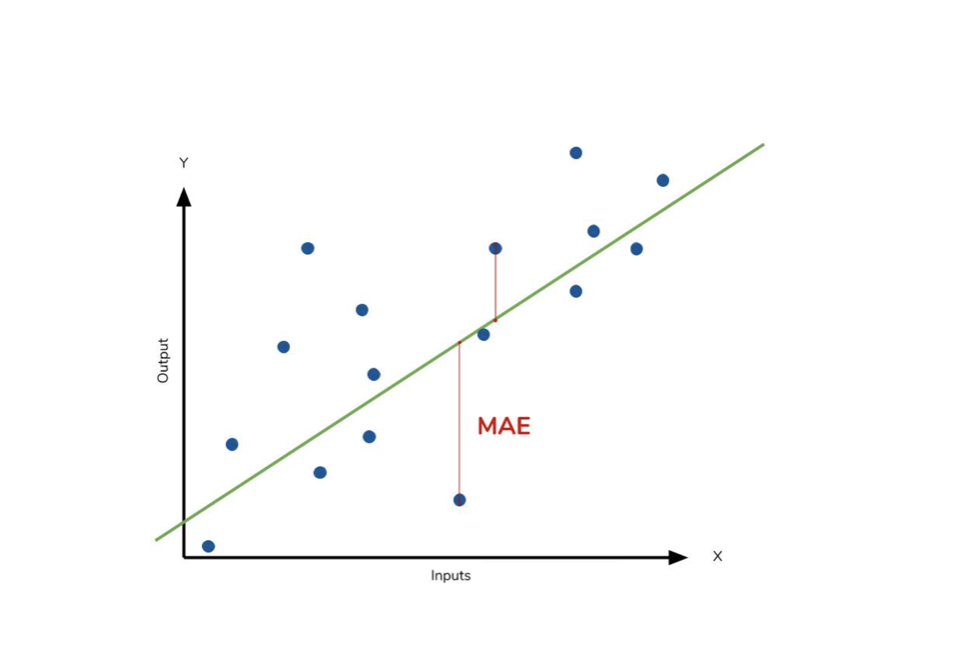
- 장점
- 지표 자체가 직관적이며 예측변수와 단위가 같다.
- ex) 기온을 예측하는 모델의 MAE가 3이라면 이 모델은 평균적으로 3도 정도를 잘못 예측하는 것임
- 지표 자체가 직관적이며 예측변수와 단위가 같다.
- 단점
- 잔차에 절댓값을 씌우기 때문에 실제 값에 대해 underestimates or overestimates 인지 파악하기 힘들다.
- ex) 삼성전자의 주가를 예측하는 모델의 MAE가 1,000이라면 이 모델이 평균적으로 주가를 1000원을 높게 예측하는지 1000원을 낮게 예측하는지 파악하기 힘들다.
- 스케일에 의존적이다. (MAE, MSE, RMSE와 동일)
- ex) 비트코인의 가격이 25,000,000이고 이더리움의 가격이 600,000 일 때 두 암호화폐의 가격을 예측하는 모델의 MAE가 동일하게 10,000 이라고 해보자. 이들은 분명 동일한 에러율이 아님에도 불구하고 MAE 숫자 자체는 동일하다.
- 잔차에 절댓값을 씌우기 때문에 실제 값에 대해 underestimates or overestimates 인지 파악하기 힘들다.
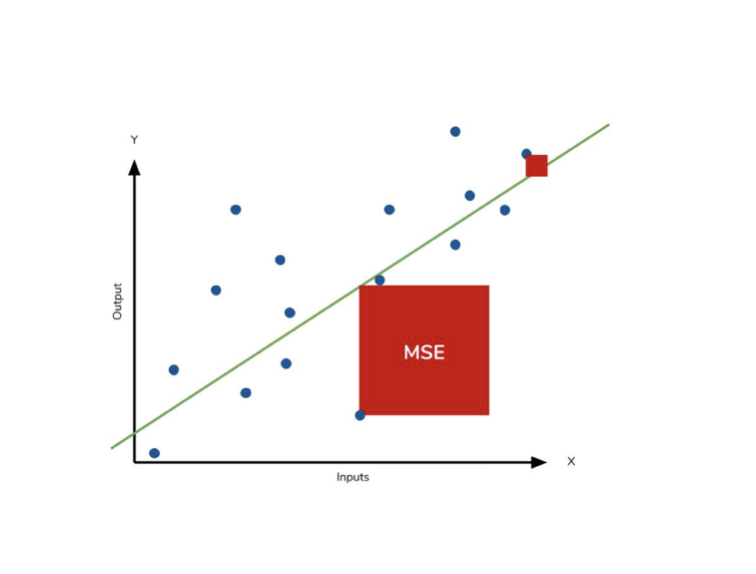
2. MSE
- 공식: 잔차의 제곱에 대한 평균
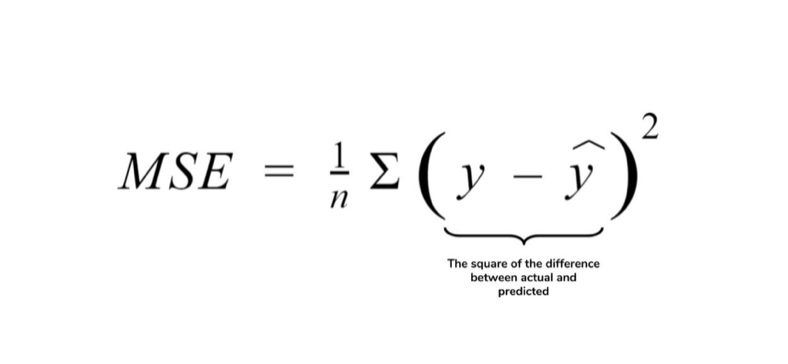
- 장점
- 지표 자체가 직관적이다.
- 단점
- 예측 변수와 단위가 다르다.
- ex) 기온을 예측하는 모델의 MSE가 4이라면 이 모델은 평균적으로 2도 정도를 잘못 예측하는 것임
* 스케일에 의존적이다. (MAE, MSE, RMSE와 동일)
- ex) 기온을 예측하는 모델의 MSE가 4이라면 이 모델은 평균적으로 2도 정도를 잘못 예측하는 것임
- 잔차를 제곱하기 때문에 이상치에 민감하다.
- 잔차를 제곱하기 때문에, 1미만의 에러는 더 작아지고, 그 이상의 에러는 더 커진다.
- 위의 그림을 참고하면, 잔차 값에 대한 제곱을 구하기 때문에(=넓이) 큰 값에 대해 벌점이 크게 매겨진다. (MSE값은 항상 MAE보다 크다.)
- 실제 값에 대해 underestimates or overestimates 인지 파악하기 힘들다.
- 예측 변수와 단위가 다르다.
3. RMSE
- 공식: 잔차의 제곱에 대한 평균 값에 루트를 씌운 것
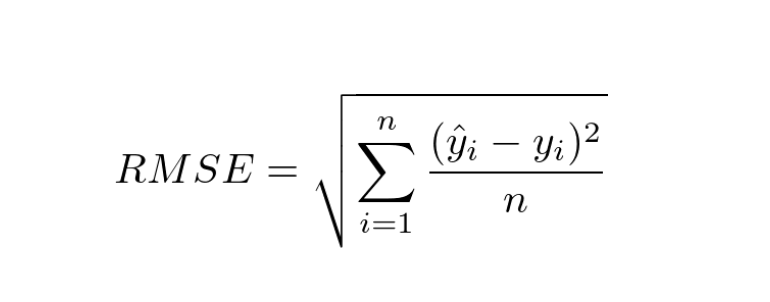
- 장점
- 지표 자체가 직관적이며 예측변수와 단위가 같다.
- ex) 기온을 예측하는 모델의 RMSE가 3이라면 이 모델은 평균적으로 3도 정도를 잘못 예측하는 것임
- 잔차를 제곱하기 때문에 이상치에 민감하다.
- 제곱된 잔차를 다시 루트로 풀어주기 때문에 잔차를 제곱해서 생기는 값의 왜곡이 MSE에 비해 좀 덜하다.
- 지표 자체가 직관적이며 예측변수와 단위가 같다.
- 단점
- 실제 값에 대해 underestimates or overestimates 인지 파악하기 힘들다.
- 스케일에 의존적이다. (MAE, MSE, RMSE와 동일)
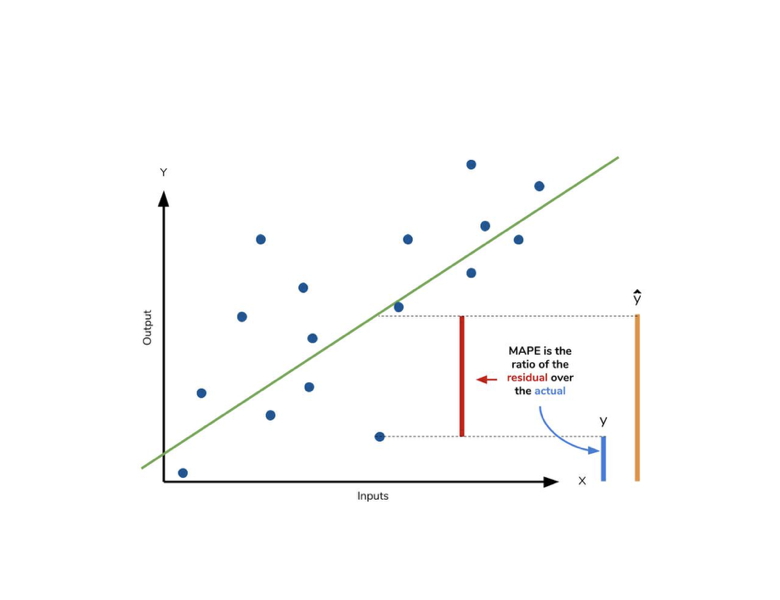
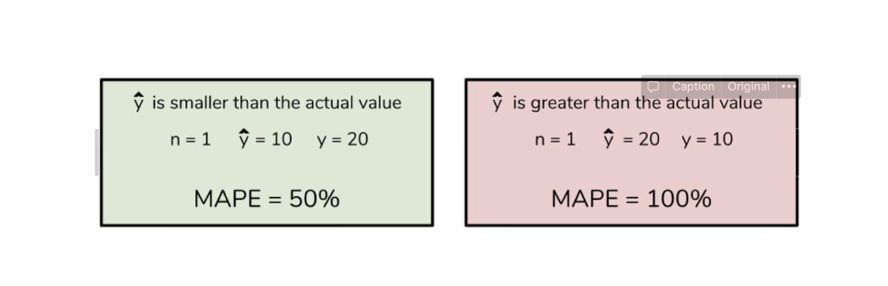
4. MAPE
-
공식: MAE를 비율(%)로 표현한 것

-
장점
- 지표 자체가 직관적이다.
- 공연석의 규모를 예측하는 모델의 MAPE가 3%인 경우 실제 공연석의 예매량과 예측 예매량 비율이 3%정도 차이난다고 해석할 수 있다.
- 비율 변수이기 때문에 MAE, MSE, RMSE에 비해 비교에 용이하다.
- ex) 비트코인의 가격을 예측하는 모델의 MAPE가 3%이고 이더리움의 가격을 예측하는 모델의 MAPE가 5% 일 때 비트코인의 가격을 예측하는 모델의 MAPE가 더 우수하다고 평가할 수 있다.
- 지표 자체가 직관적이다.
-
단점
-
실제 값에 대해 underestimates or overestimates 인지 파악하기 힘들다.
-
비율로 해석이 의미있는 값에만 적용할 수 있다.
- ex) 기온을 예측하는 모델의 경우 MAPE로 해석하기 힘들다.
-
실제 값에 0이 포함될 경우 MAPE를 계산할 수 없다.
- 예를 들어 10분 간격으로 서울시의 따릉이 수요를 예측해본다고 해보자. 이 때 10분의 interval 동안 수요가 0인 구간이 존재한다면 MAPE는 zero-division error를 반환한다. 이를 보완하기 위해 과수요 구간 (ex, 10분간 수요가 100대 이상인 구간의 MAPE는 20%이다. 라는 숫자를 뽑아볼 수 있다.)
-
5. MPE
- 공식: MAPE에서 절댓값을 제외한 지표
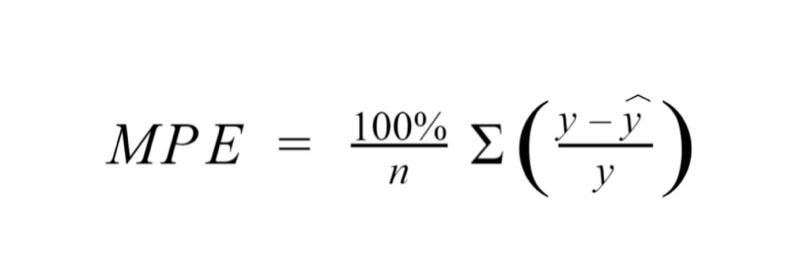
- 장점
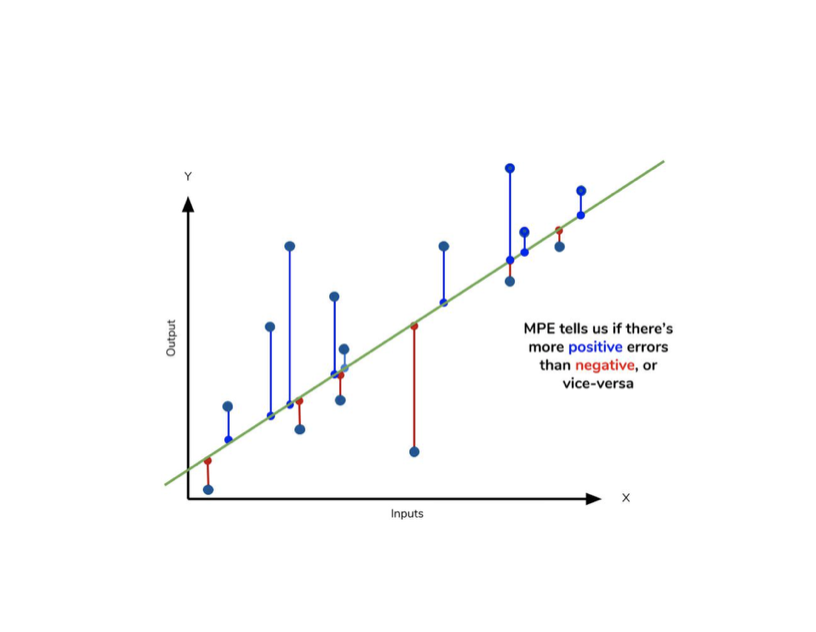
- 실제 값에 대해 underestimates or overestimates 인지 파악할 수 있다.
- MPE > 0: underperformance (underestimates)
- MPE < 0: overperformance (overestimates)
- 실제 값에 대해 underestimates or overestimates 인지 파악할 수 있다.
- 단점
- 지표 자체가 직관적이지 않으며 예측변수와 단위가 다르다.


평가지표에 대해서 공부할 수 있는 정말 좋은 글 감사합니다~ ^^