[선형대수학] Linear Algebra

회사에서 공부하는 바탕을 가지고 정리를 함

vector

• scalar 와 달리 크기와 방향을 모두 가지는 양
• v = [a, b] 로 나타낼 수 있고 a, b는 벡터의 성분(component)라고 함. 즉, v가 벡터

vector norm

• 어떤 벡터를 길이나 사이즈같은 양적의 수치로 mapping 하기 위한 함수$(||.||: V->R)$
  다음 세가지 조건을 만족해야함

1. $||u+v|| <= ||u|| + ||v||$
2. $||av|| = |a| ||v||$
3. If $|v|| = 0,$ then $v = 0$

L1 norm

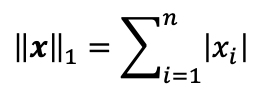
L2 norm

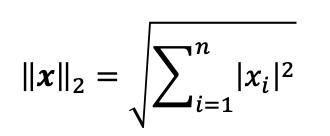
infinity norm

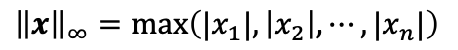
• infinity norm은 아래와 같이 p가 무한대일 때를 의미한다.

p-norm

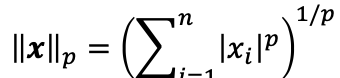
Linear Dependency

vector X = { $x_1$, $x_2$, ... , $x_n$} 이 주어졌을 때,
$a_1x_1 + a_2x_2 + ... + a_nx_n = 0$ 으로 linear combination 을 나타낼 수 있다.

여기서 $a_1, a_2, ... , a_n$의 값이 하나라도 nonzero이면 linear dependency 라고 한다.

Linear independent

+추가적으로,

• Linear independent는 $R^n$ 공간에서 vector {$v_1, ...v_p$} 가 있을 때,
  벡터 방정식이 trivial soltuion를 가지고 있을 때 linear independet 하다고 말한다.
• trivial soltuion (자명해)
  free variable이 없는 것을 의미

Orthogonal vector

• 2개의 vector가 주어졌을 때 두 vector가 서로 수직이면 otrhogonal 하다고 말한다.
  두 벡터의 스칼라는 0.
  

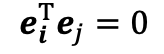
Normalized vector

• 정규화는 무언가를 표준화 시키거나 다른 것과 비교하기 쉽도록 바꾸는 것을 의미
• 다른 것들과 비교하기 위해 표준화 시킨 벡터들의 크기를 1로 규정
  

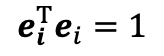
Matrix

• A 가 $m$x$n$ 행렬이면 i번째 행, j번째 열에 있는 스칼라 항목은 $a_{ij}$ 로 표기한다
  
  위와 같이 notation으로 나타낼 수 있음

Rank of Matrix

행렬 A의 rank는 $rank(A)$ 로 표시하고 다음과 같다.

• 행렬의 일차독립인 행 또는 열의 최대 개수
• 행렬 A의 pivots 의 개수

ex 1

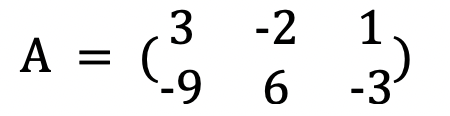
$A$ marix 같은 경우에는 1열과 3열은 $(1, -3)$으로 서로 종속인 것을 확인할 수 있다. 2열 같은 경우에는 $(-1, 3)$ 으로 (1, -3)과 같은 방향에 놓아져 있지 않아 $A$의 최대 열 개수가 2개라 판단하여 $rank(A) = 2$ 라고 할 수 있다.

ex 2

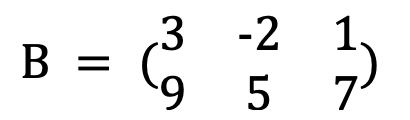
$B$ Matrix 같은 경우에는 열로 보았을 때 $(1, 3), (-2, 5), (1, 7)$ 로 같은 수직선 상에 있지 않아 $rank(B) = 3$ 이다.

Matrix inversion

• 2차원 행렬의 inversion
  

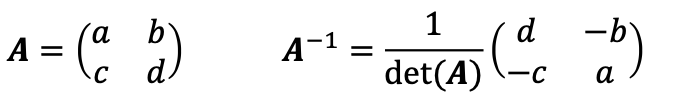
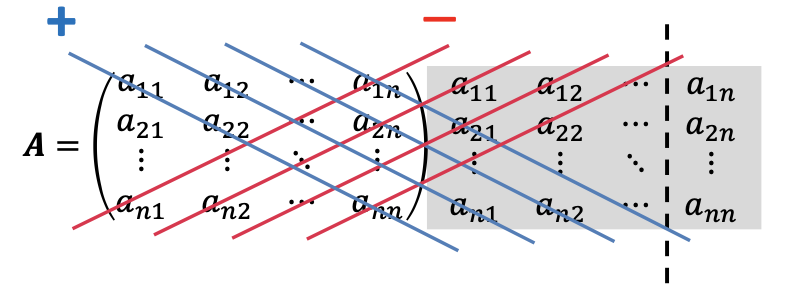
Determinant

• 행렬의 계산식