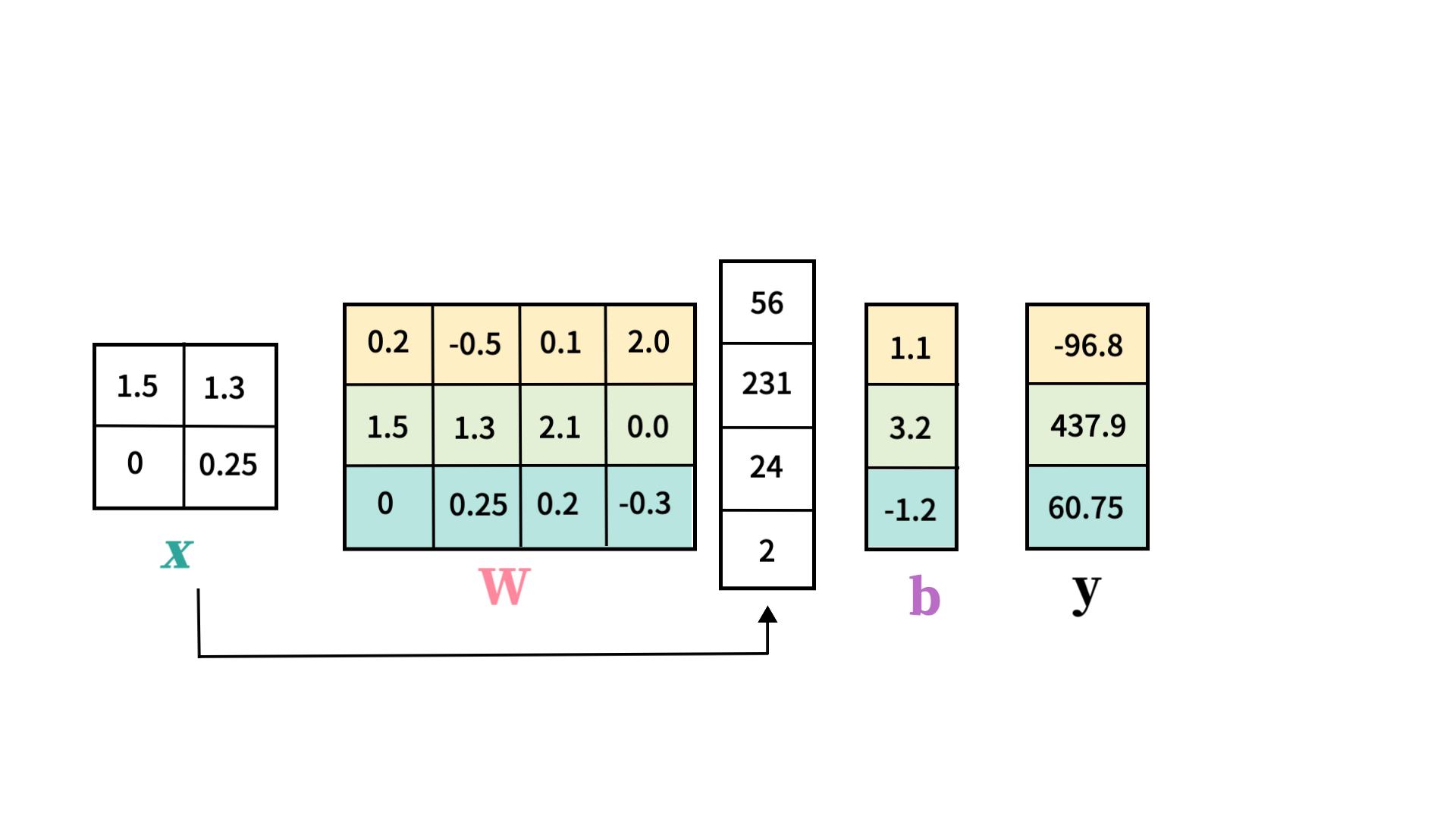
Linear Classifier

• 등장 배경: NN Classifier(가장 가까운 학습 데이터를 찾아 예측을 수행하는 알고리즘)의 한계를 극복하고자 parametric approach 사용.
• 이미지를 10개의 카테고리 중 하나로 분류하는 Task가 있다고 가정해보자.
• y=Wx+b라는 간단한 선형함수를 세워두자.
• 여기서 각 레이블이 올바른 이미지에 대해 가장 높은 점수를 받도록 W(Weigth Parameter)가 정해져야 한다.

차원 계산하기

• 각 term의 차원을 계산해보자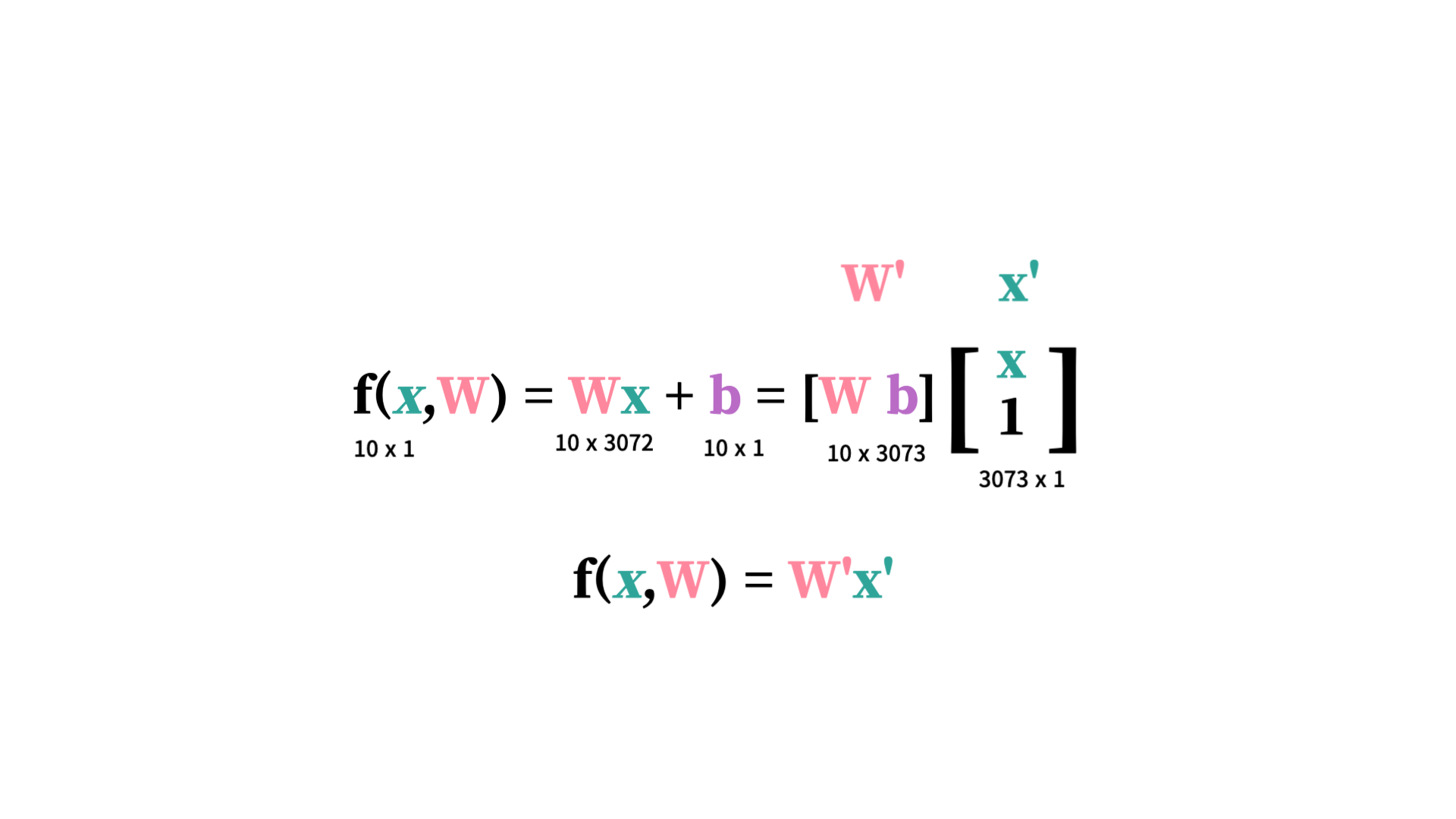f(x,W) = Wx+b

• 이미지 크기 = 32x32x3 (3072)

• x: 3072 x 1로, 이미지를 1차원을 flatten한 것이다.

• output: 10 x 1(10개의 클래스를 분류)

• W: 10x3072(행렬곱 규칙에 따라)

• b: 3072x1(bias term; input에 영향을 주지 않고 output에 영향 미침)

  • 편향의 역할:
    데이터 레이블이 이분하게 분포하지 않고, 하나의 클래스에 치중되어 있는 경우가 있다(skewed distribution). 이럴 경우 나머지 parameter가 데이터 분포가 아닌 데이터 본연의 특성에 집중할 수 있도록 돕는 것이 bias term이다.
    • 예를 들어, training 데이터에 고양이가 많은 경우 데이터를 보지 않고도 '일단은' 고양이라고 예측하는 방향으로 작용한다. 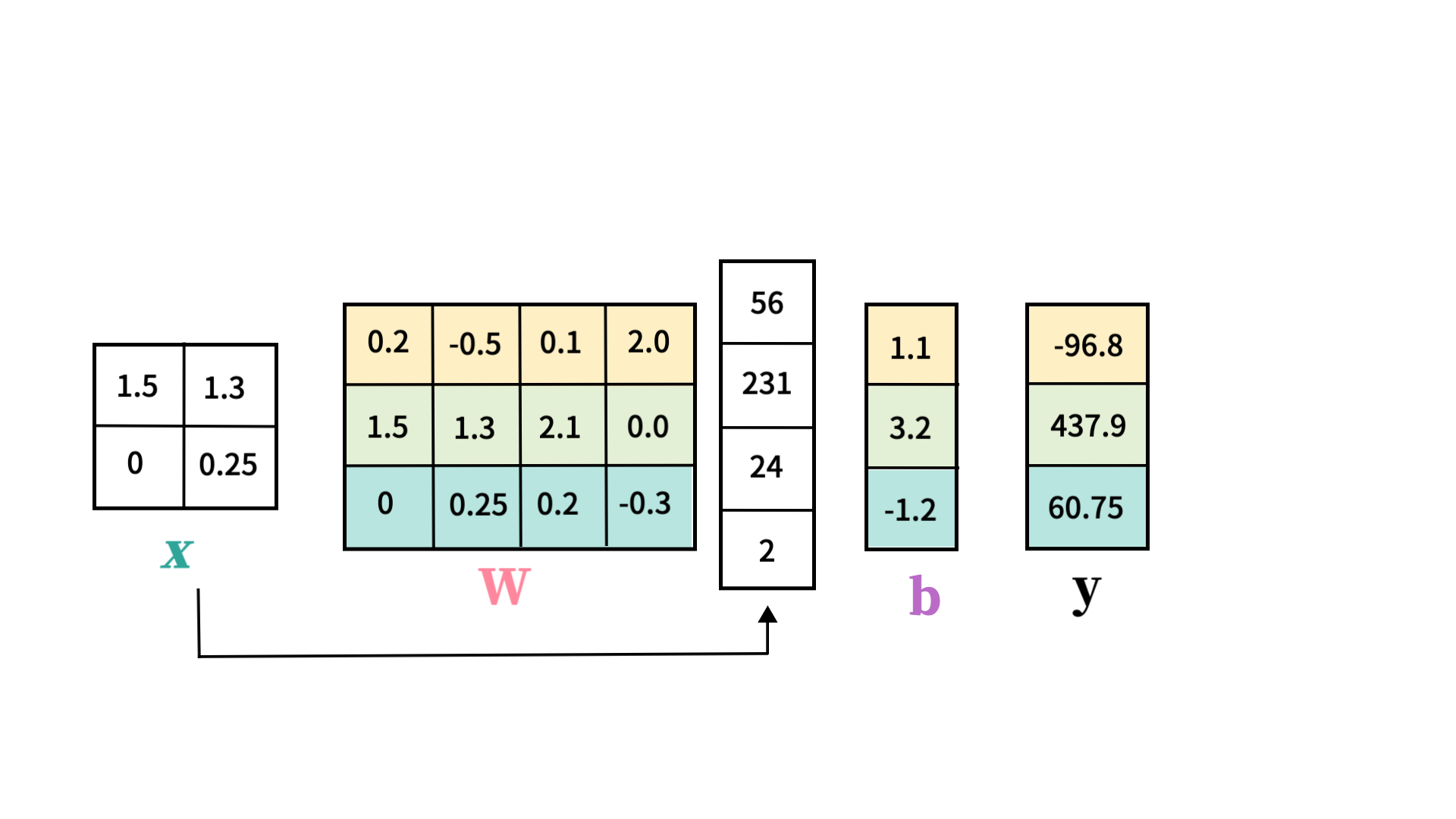→ W라는 행렬의 각 row는 각 레이블(클래스)의 weight라고 해석 가능

Softmax Classifier

• 등장 배경 : y는 점수. 근데 이 점수는 해석이 어렵다. 따라서 0과 1 사이의 경계 점수를 얻어서 확률로 해석할 수 있다면 더 좋을 것. 크게 2가지의 activation function이 있다.
• 시그모이드 : binary classification에 쓰임
  
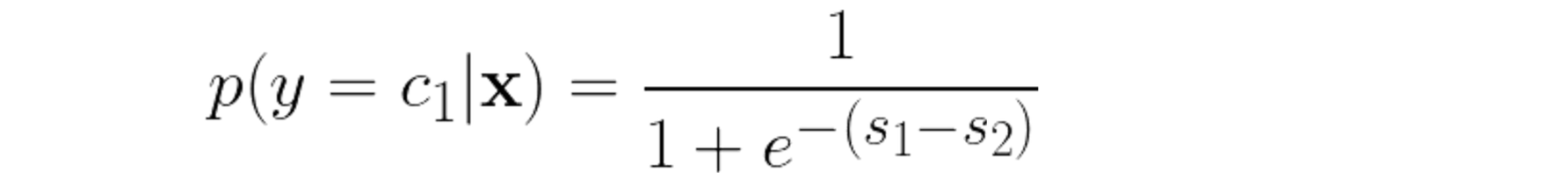
• softmax : multi-label classification에 쓰임
  

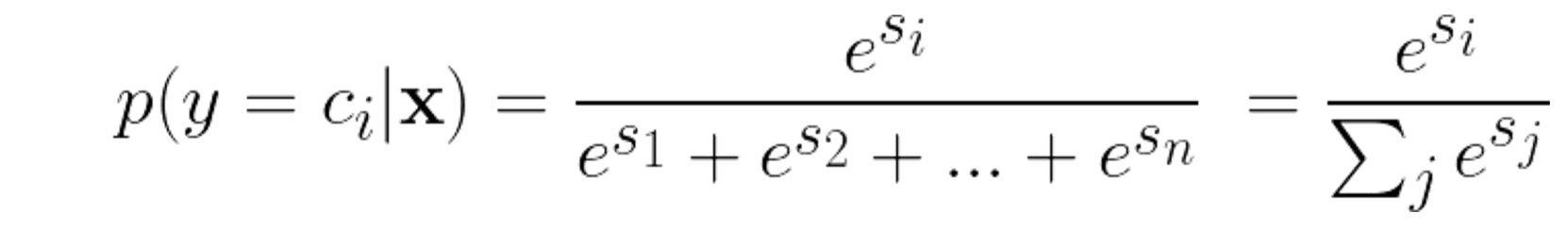
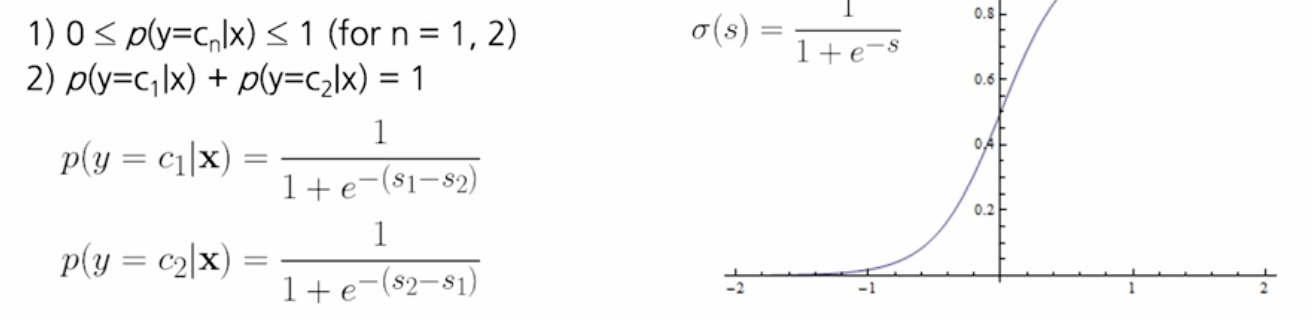
Softmax Classifier 출력 확률의 수치적 불안정성 방지를 위한 방법

[문제] 소프트맥스 함수에서 지수화를 할 때 큰 수를 다루게 되면 수치적 불안정성이 발생할 수 있음
[해결] 입력 값의 최대값을 계산하여 모든 입력 값에서 이를 빼는 것입니다. (가장 큰 값이 0이 됨)

Loss Function

Discrete Loss Function

몇 가지 단점이 있어 주로 사용되지는 않음

1. 마진 기반 손실 (Margin-Based Loss):

   • 모델이 잘못된 예측을 했을 때 일정한 손실 값을 부여
   • 올바른 예측을 했을 때는 손실이 0
   • 따라서 이로 인해 미분 불가능하다는 단점이 존재 → 최적화 과정에서 제약으로 작용

2. 로그 손실 (Log Loss):

   • 모델의 예측이 정확할수록 손실 값이 낮아지고 미분 가능 → 최적화에 용이

3. 지수 손실 (Exponential Loss):

   • 로그 손실과 유사 잘못된 예측에 대해 더 큰 손실(페널티)을 부여(올바른 예측에 대해서는 반대)

4. 힌지 손실 (Hinge Loss):

   • 오류에 대한 loss가 선형적으로 증가
   • 정답에 가까운 예측에도 약간의 페널티 부여
   • SVM에서 사용(결정 경계에 가까운 데이터 포인트를 더욱 신중하게 다루는 것)

Cross Entropy Loss

사실 ML에서는 주로 확률적 손실 함수를 사용.

크로스 엔트로피
→ 모델의 예측 확률과 실제 라벨 간의 차이를 측정
→ 활성화 함수와 결합되어 사용됨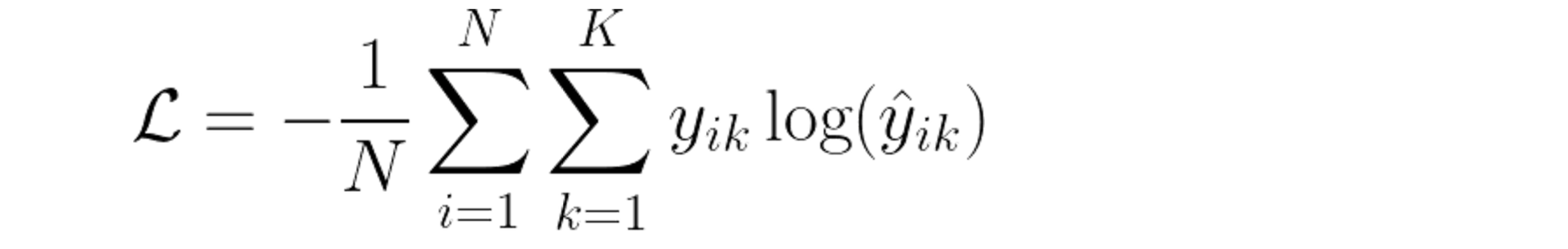

KL Divergence

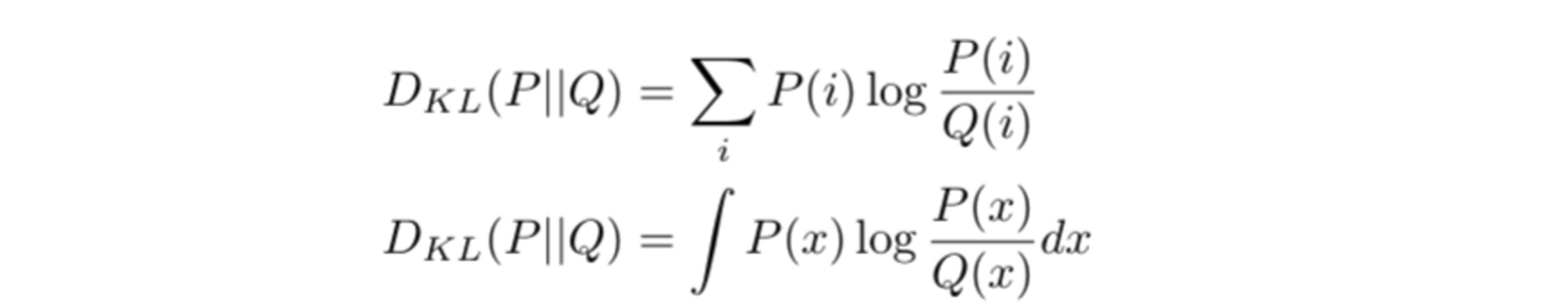KL Divergence는 두 확률 분포 사이의 차이를 측정하는 데 사용됩니다. 이 값이 작을수록 두 분포가 유사함을 나타내며, 이는 모델이 실제 데이터 분포를 얼마나 잘 따라가고 있는지를 평가하는 데 유용합니다.

최적화(Optimization)

: loss function(cost function, J())값을 이용해 parameter의 값을 update 하는 방법

1. 완전탐색, 랜덤탐색 → 잘 안됨

2. 그리디 탐색 → 나머지 weight parameter는 고정, 하나의 weight parameter 바꿔가면서 optimize → 두개 이상의 파라미터가 동시에 바뀌는 경우를 고려하지 않기에 잘 안된다고 함

3. Gradient Descent와 SGD
   Gradient Descent는 산의 최정상으로 올라가기 위해서, 현재 위치에서 가장 가파른 방향으로 발을 디디는 것과 같다.BUT 몇가지 한계를 가진다.

• 볼록하지 않은 표면: 로컬최적점/새들 포인트에 빠질 수 있음
• 미분 가능성: cost function이 미분 가능한 경우에만 적용 가능
• 수렴 속도: 국부 최솟값으로 수렴하는 것의 속도가 느리다 (모든 방향에 대해 발을 디디는 것이니까)

그래서 사실 주로 확률적 경사 하강법(SGD, Stochastic Gradient Descent)을 사용.

• 일부 데이터에 대해서만 gradient descent 수행해서 속도 UP

Linear Classifier가 잘 안쓰이는 이유?

성능이 별로 좋지 않음

• 시각적으로 해석하자면, 각 클래스당 하나의 템플릿(weight parameter)만 학습이 가능하다
• 기하학적으로 해석하자면, linear한 decision boundary 만 생성할 수 있다

Featurization: linear boundary로는 해결못하는 분류 task 수행 가능

Featurization: 선형 경계로 해결할 수 없는 분류 작업

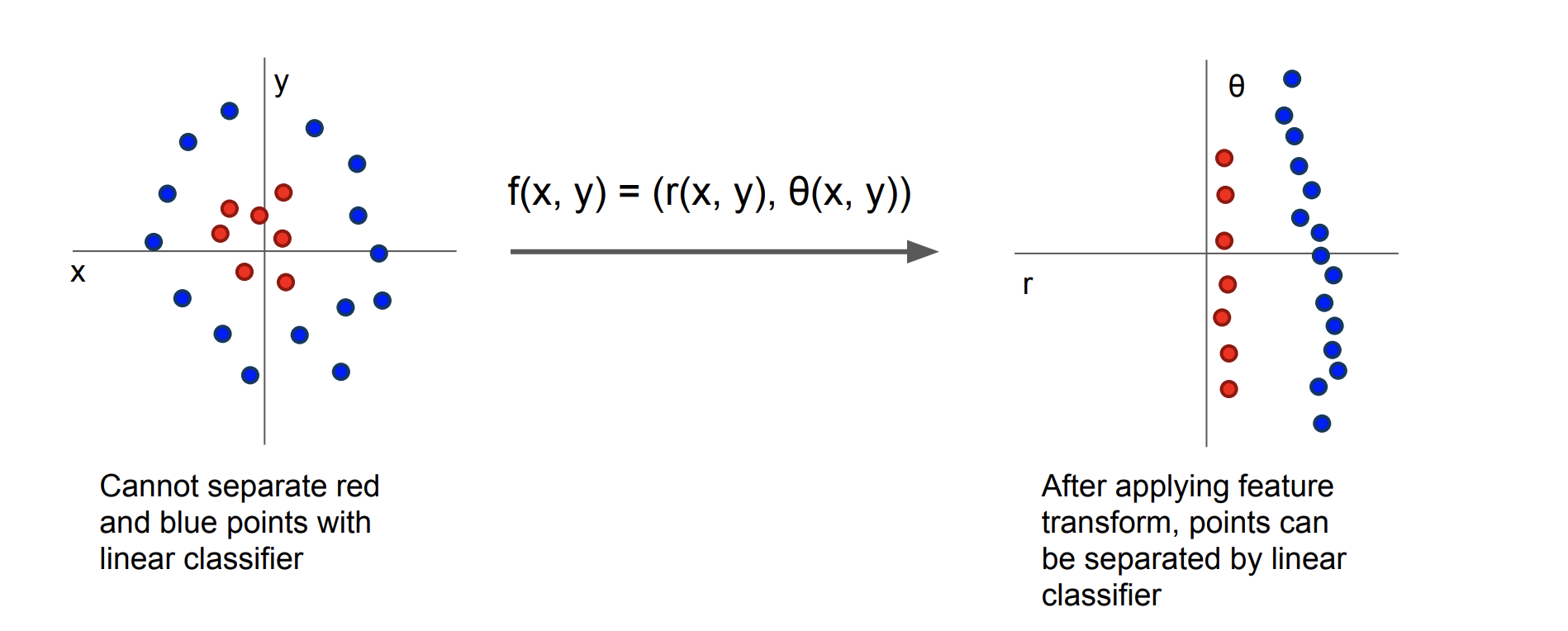*출처: https://cs231n.stanford.edu/slides/2017/cs231n_2017_lecture3.pdf
원본 feature space를 조작해 선형경계로 해결 불가능한 classification을 수행
1. 고차원 매핑: ex) 2차원 → 3차원
2. 비선형 변환:
3. 커널 트릭: SVM에서 사용
4. rule based featurization: 도메인 지식을 이용해 손으로 한땀한땀하는 rule based 특성화과정. 요즘엔 안쓰임.

💬
아무리 featurization을 해도 여전히 구리다 linear classification은!
Activation Function이랑 Loss Function 헷갈리지 말기