
신경망 관점에서의 선형 회귀
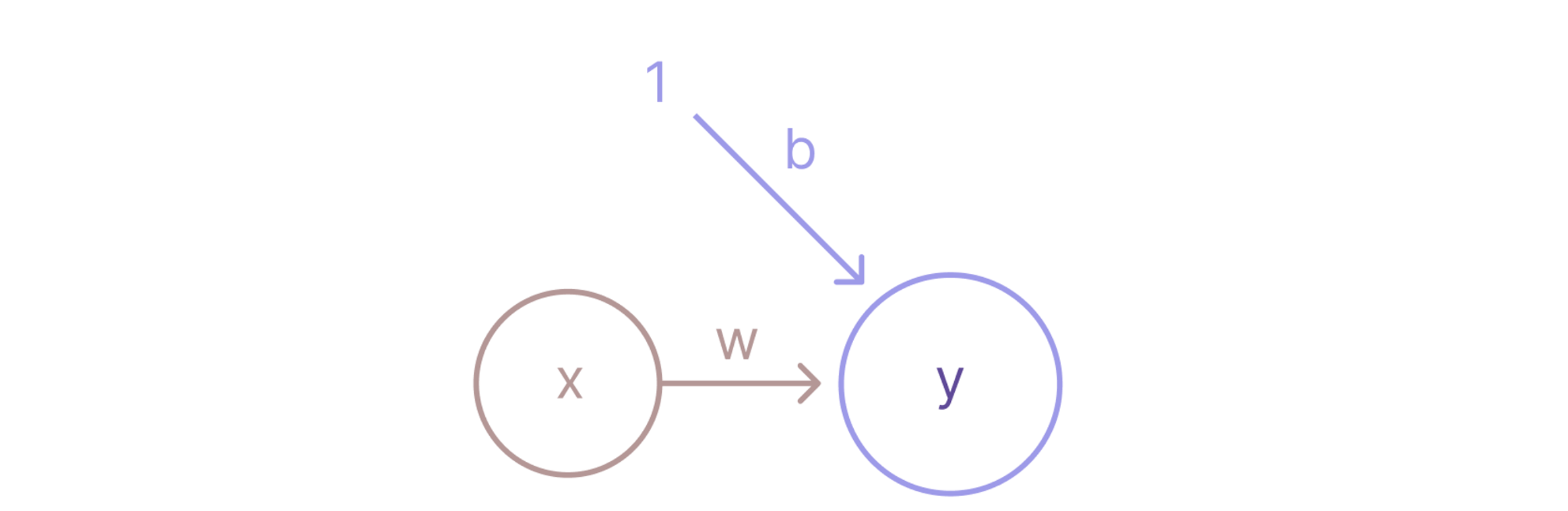
단순 선형 회귀를 전통적인 방법에서 벗어나 신경망 관점에서 바라본다면, 위의 그림처럼 도식화할 수 있다. 이 접근방식이 꽤나 흥미로웠음!
그림의 내용을 한마디로 요약하자면 입력층의 독립변수(특징변수) x가 출력층의 예측 변수 y로 로 mapping되는 것이다. Mapping되는 과정에서 가중치 w와 bias b가 사용되는데, 얘네들이 parameter 즉 모델의 학습 대상이다. 입력층의 독립변수들은 각각 하나의 뉴런에 해당되겠다.
*아래에는 선형회귀 모델 구현ㅇ르 위해 알아두어야 할 몇가지 기본 개념들을 복습차원에서 다시 정리해두었다.
상관계수 분석
선형회귀 모델을 세우기 전, 두 변수 사이에 유의미한 선형 관계가 존재하는지 상관계수 분석을 통해 확인할 수 있다. 아래 기준을 참고하면 좋을 것 같다. 물론 절대적인 건 아니다.
- |상관계수|의 값이 -라면 선형 관계성은,
- 0.0 관계 없음
- 0.0~0.2 매우 낮음
- 0.2~0.4 낮음
- 0.4~0.6 다소 높음
- 0.65~0.85 높음
- 0.85~1.0 매우 높음
- 1.0 일치
다중선형회귀 모델에서 독립 변수들 간의 상관관계를 파악하는 데 유용하다. 특히, 다중공선성을 확인하는 데 도움을 줄 수 있다.
numpy의 np.corrcoef()를 사용해 쉽게 계산할 수 있다. 해당 함수는 argument로 배열 또는 리스트를 받아 상관행렬을 반환한다.
correlation_matrix = np.corrcoef(x, t) # 상관행렬 구하기
correlation_coefficient = correlation_matrix[0, 1] # 상관행렬에서 특정 요소 뽑기이 외에도 시각화(scatterplot)를 통해 독립변수 간의 다중공선성을 확인하는 것도 직관적이고 좋다. plt.scatterplot사용하면 됨
경사하강법
이론
목적 경사하강법의 목적은 주어진 파라미터의 최적값을 찾는 것이다.
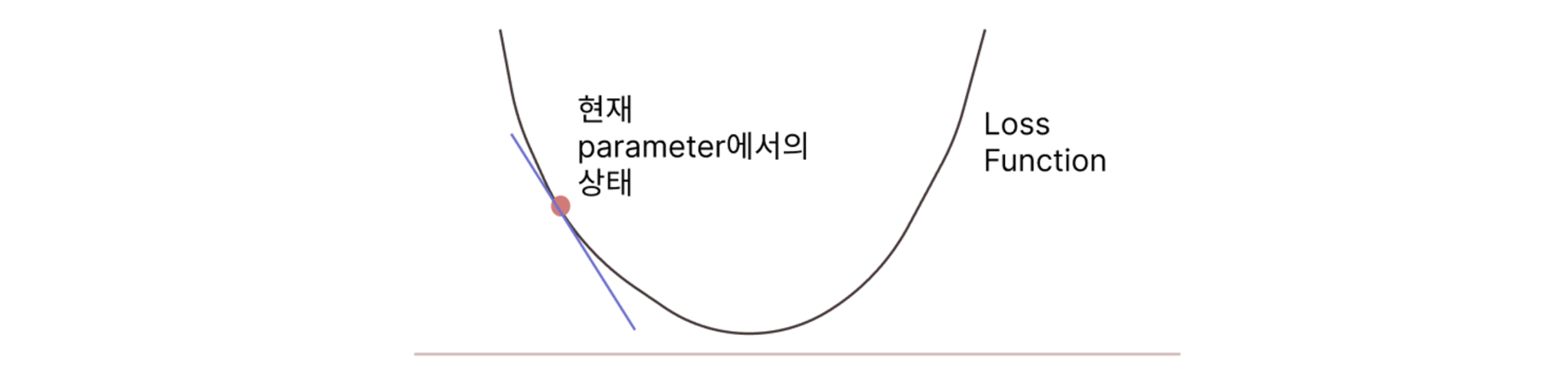
대상 함수 이를 위해 Loss Function, 즉 파라미터 값에 따른 Loss의 변화를 다루는 함수를 대상으로 한다.
작동 방식 먼저 특정 파라미터 값에서 Loss 함수의 기울기(gradient)를 계산하고, 그 기울기의 반대 방향으로 파라미터를 학습률만큼 업데이트하는 과정을 반복한다.
PyTorch 메서드(암기!)
loss.backward()
→ 현재의 parameter에 대한 loss function의 graident를 계산한다. 이 기울기는 각 파라미터에 대해 optimizer에 저장된다.
optimizer.step()
→ 계산된 gradient로 parameter 업데이트한다
optimizer.zero_grad()
→ 이전 단계에서 계산된 경사(기울기) 초기화한다. 기울기는 누적되는 성질이 있기에 이전 단계가 새 단계에 영향을 주는 것을 막아야한다. 따라서 이전 미니배치에서 계산된 기울기를 초기화하여 정확한 gradient 계산을 할 수 있도록 한다.
위 세가지 메서드를 순서대로 반복적으로 수행함에 따라 최적의 파라미터에 근접할 수 있다.
배치 경사하강법의 단점
- Local minima 문제 : 계산이 정확하고, 안정적이지만 전체 데이터셋의 기울기를 평균을 내어 계산하므로 지역적인 최소값에 빠질 가능성이 높다
- 높은 계산 비용 문제
그래서 등장하는 것이 '확률적 경사하강법'
확률적 경사하강법(SGD)
모든 데이터의 오차를 계산하는 방식으로 접근하지 않고, 각각의 데이터 포인트마다 오차를 계산하는 방식이다.
SGD의 장점 말할 때 쓰기 좋은 표현이있는데, 그건 바로 ‘노이즈’
- 각 데이터 포인트의 기울기를 계산하므로 → 기울기 계산에 노이즈가 포함된다 → 이 노이즈는 최적화 과정에서 로컬 미니마를 탈출에 용이하다! (+계산 비용이 적고 빠르게 수렴할 수 있다)
SGD는 optim 라이브러리에서 불러와 구현할 수 있다.
import torch.optim as optim
optimizer = optim.SGD(model.parameters(), lr = 0.01) # optimizer 정의이 때 model.parameters() 메서드는 우리가 지정한것이 아닌, 아니면 부모 클래스인 nn.Module에서 지정한 것이다.모델의 학습 대상이 되는 모든 파라미터를 옵티마이저에게 전달하는 역할을 한다.
위 코드를 실행하면 내부적으로 일어나는 일은?: 모델의 파라미터들(가중치들, 편향들)과 학습률(0.01)을 전달받은 옵티마이저 객체가 생성된다. SGD알고리즘을 사용하는!(참고로 옵티마이저가 정의되기 위해서는 모델의 파라미터 상태, 옵티마이저 알고리즘, 학습률이 전달되어야 한다)
에폭
Epoch: 모델이 전체 데이터셋을 한 번 완전히 학습하는 과정
0부터 시작하는 것에 유념하자.
데이터 표준화
: 한마디로 스케일링
근데 생각보다 유의해야 하는 부분이 있다.
1. 학습/평가 때 사용하는 스케일러에 유의하기!
학습시, 스케일러를 반드시 학습 데이터 대상으로 계산하고 학습 데이터를 변환하여 사용한다. 평가시, 평가 데이터가 아닌! 학습 데이터 대상으로 계산한(fit한) 스케일러를 사용해 테스트 데이터를 변환하여 사용한다.
2. 변수형에 유의하기(배열/텐서)!
StandardScaler는 2차원 numpy 배열을 입력으로 받는다. 따라서 기존에 tensor를 사용했다면 tensor.numpy()를 통해 numpy로 변환해줘야 한다. 또한 차원이 1차원 배열이이라면 reshape 해줘야 한다.(물론 view쓰고 나서 넘파이로 바꿔도 된다)
# 텐서를 numpy 배열로 변환
numpy_array = tensor.numpy()
# 1차원 numpy 배열을 2차원으로 변환 (예: (3,) -> (3, 1))
numpy_array_2d = numpy_array.reshape(-1, 1)reshape에서 -1은 열크기에 따라 행 크기를 자동 계산 한다는 것이다(매우 유용한 방법)
이후에는 torch를 사용해야하므로, 표준화한 다음에는 numpy를 다시 tensor로 변환해준다.
데이터 표준화를 사이킷 런으로 진행하는 과정은,
- 모듈 불러오고
- 스케일러 객체 생성
- 스케일러 객체로 2차원 배열 표준화
# 사이킷런의 StandardScaler 모듈 불러오기
from sklearn.preprocessing import StandardScaler
# 객체를 생성(먼저 인풋 피처에 적용해보자)
scaler_x = StandardScaler() # StandardScaler 객체를 생성
# 2차원 행렬로 reshape한 다음 데이터 표준화
x_scaled = scaler_x.fit_transform(x.reshape(-1, 1))
# 레이블 피처도 마찬가지 방법으로 진행
scaler_t = StandardScaler()
t_scaled = scaler_t.fit_transform(t.reshape(-1, 1))- 데이터를 표준화한 numpy 배열을 2차원 Tensor로 변환하기
- view메서드를 사용해주면 됨!
- contiguous조건이 만족되는 경우에는 reshape이 아닌 view를 사용하는 것이 메모리 관리 차원에서 좋다.
x_tensor = torch.tensor(x_scaled, dtype=torch.float32).view(-1, 1)
t_tensor = torch.tensor(t_scaled, dtype=torch.float32).view(-1, 1)