그래프 (Graph)
특징
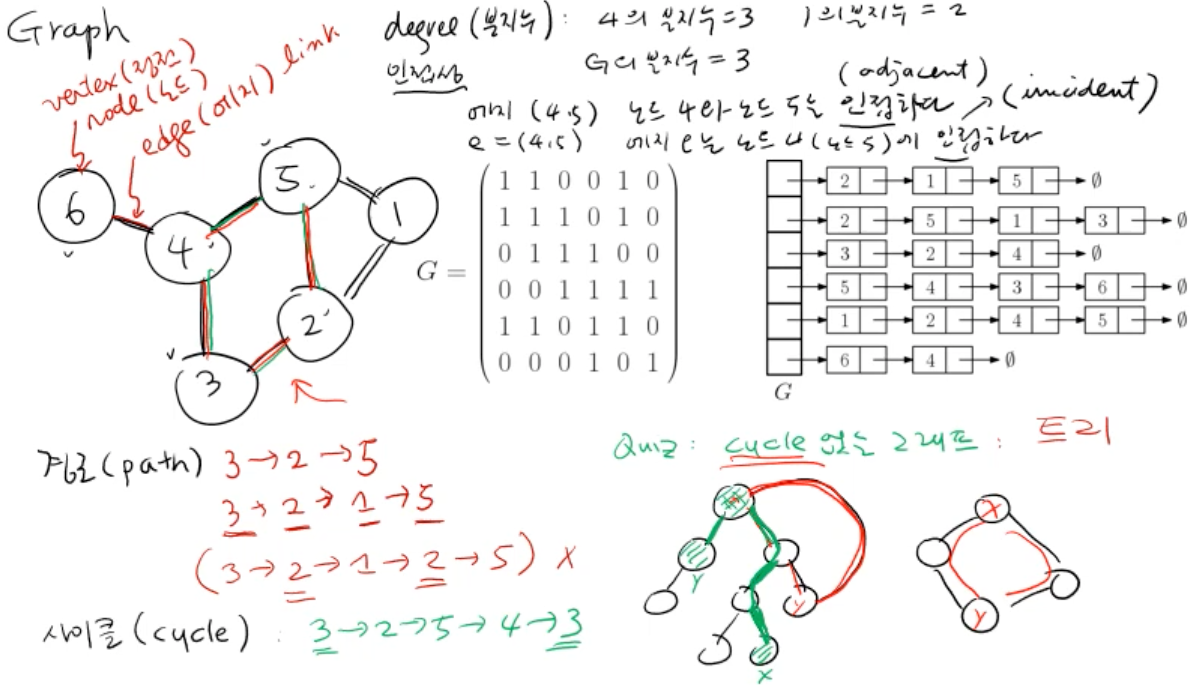
- G = (V, E) (vertex (정점), edge (간선))
- 가장 복잡한(일반적인) 자료구조
- degree (분지수): 해당 노드에서 뻗어 나가는 간선의 수 중 가장 큰 수
- 인접성 (adjacent): ex) e(4, 5) 노드 4와 노드 5는 adjacent하다
- 인접성 (incident): ex) e(4, 5) 해당 edge는 노드 4와 노드5에 incident하다
- 경로 (path): 출발 노드에서 도착 노드까지 경로는 중복 노드가 있으면 안된다.
그래프 vs 트리
- 사이클 (cycle): 해당 노드에서 출발해서 돌아올 때 까지 닫힌 경로
(사이클이 없는 그래프 = 트리) - 트리: 출발 x에서 도착 y까지 가는 경로는 하나밖에 존재하지 않는다.
표현법
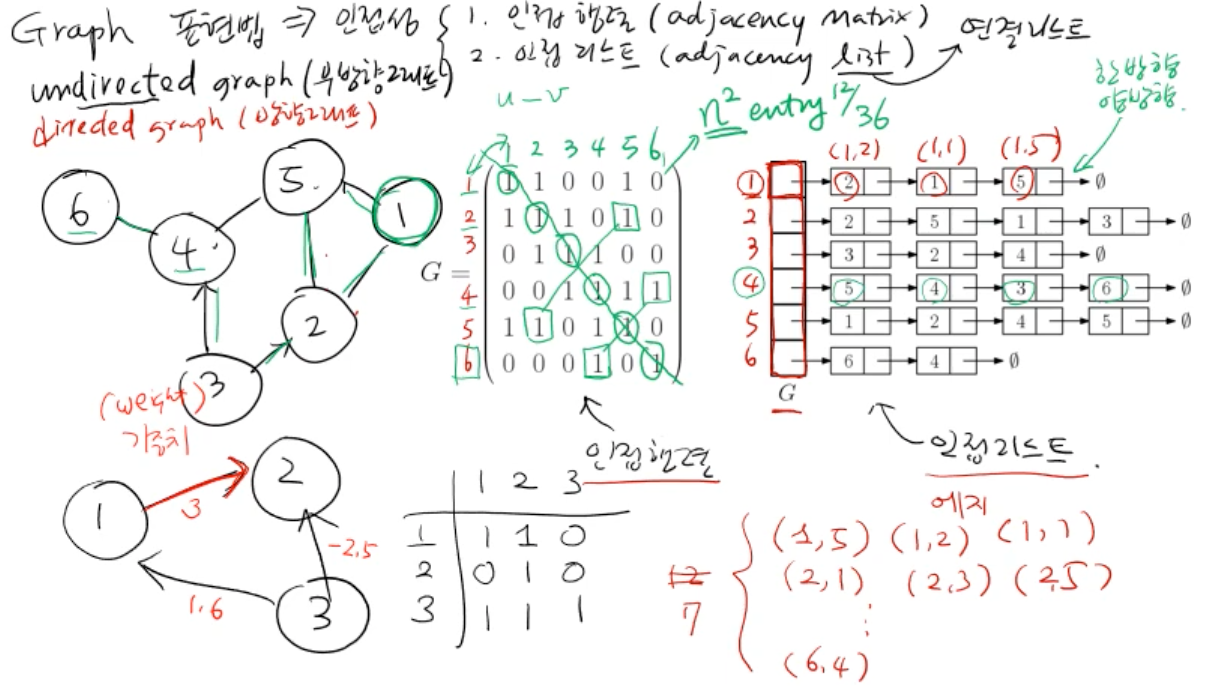
- 인접 행렬: 2차원 배열의 형태, n^2의 행렬에서 표현되는 edge는 e x 2 따라서 그 외(n^2 - e x 2)의 메모리 낭비가 심하다 개선 -> 인접 리스트
- 인접 리스트(여기서 리스트는 링크드리스트): 표현할 때 edge의 순서는 상관없다 ex) 5 -> 4 -> 3-> 6
- edge에 direction이 없는 그래프: undirected graph (무방향그래프)
- edge에 direction이 있는 그래프: directed graph (방향그래프)
- 가중치 (weight): edge를 통해 노드로 이동할 때 드는 비용이라고 생각하면 된다.
| 인접 행렬 | 인접 리스트 | |
|---|---|---|
| 1. memory | O(n^2) | O(n + m) |
| 2. E(u,v)exist? | G[u][v] > 0? O(1) |
G[u].search(v)? O(n) |
| 3. u에 인접한 모든 노드 v에 대해 |
O(n) | O(인접노드수) |
| 4. insert E(u,v) | G[u][v] = 1 O(1) |
O(1) |
| 5. delete E(u,v) | G[u][v] = 1 O(1) |
O(1) |
1. memory? 인접행렬: n^2, 인접 리스트: n(node 수) + m(edge 수)
2. 노드 u, v에 연결된 edge? 인접행렬: O(1), 인접 리스트: O(n) (최악의 경우)
(줄줄이 소세지마냥 한 노드에 다 연결되어 있는 경우)
3. u에 인접한 모드는 노드 v에 대해 동작할 경우? 인접행렬: O(n), 인접 리스트 O(n)
4. 새로운 edge 삽입? 인접행렬: O(1), 인접 리스트: G[u].pushfront(v) O(1)
5. 기존 edge 삭제? 인접행렬: O(1), 인접 리스트: O(n)3번의 경우 인접 행렬은 노드간 연결이 없어도 O(n)시간이 걸린다, 인접 리스트는 head부터 None까지 가기 때문에 인접한 노드 수만큼 수행하게 된다.
따라서, 메모리 측면에선 인접 리스트가 좋지만, 속도 측면에서는 인접 행렬이 더 빠르다 (단, m이 무수히 많지 않은 경우)
- 노드의 개수에 비해 edge가 적을 경우 sparse 그래프 <-> dense 그래프
- 파이썬의 경우 연결리스트가 아닌 list를 사용해도 무방, pushfront -> append
DFS (Depth First Search)
특징
- 방문 노드의 인접 노드의 방문을 진행할 때, 방문 여부를 체크하며 leaf노드까지 방문 후 방문하지 않았던 노드를 다시 탐색한다.
- Stack을 사용한다.
- back edge의 존재는 cycle이 존재한다는 의미이다.
- back edge = 그래프 상에서 연결된 edge이지만 이미 탐색을 완료한 노드라 사용하지 않은 edge
- pre_time 과 post_time의 포함관계를 통해 DFS tree를 만들 수 있고, 부모노드와 자식노드의 관계를 알 수 있다.
장점
- 현 경로상의 노드들만 기억하면 되므로 저장공간 수요가 비교적 적다
- 목표 노드가 깊은 단계에 있을 경우 해를 비교적 빨리 구할 수 있다.
단점
- 해가 없는 경로가 깊을 경우 탐색 시간이 오래 걸릴 수 있다.
- 얻어진 해가 최단 경로가 된다는 보장이 없다.
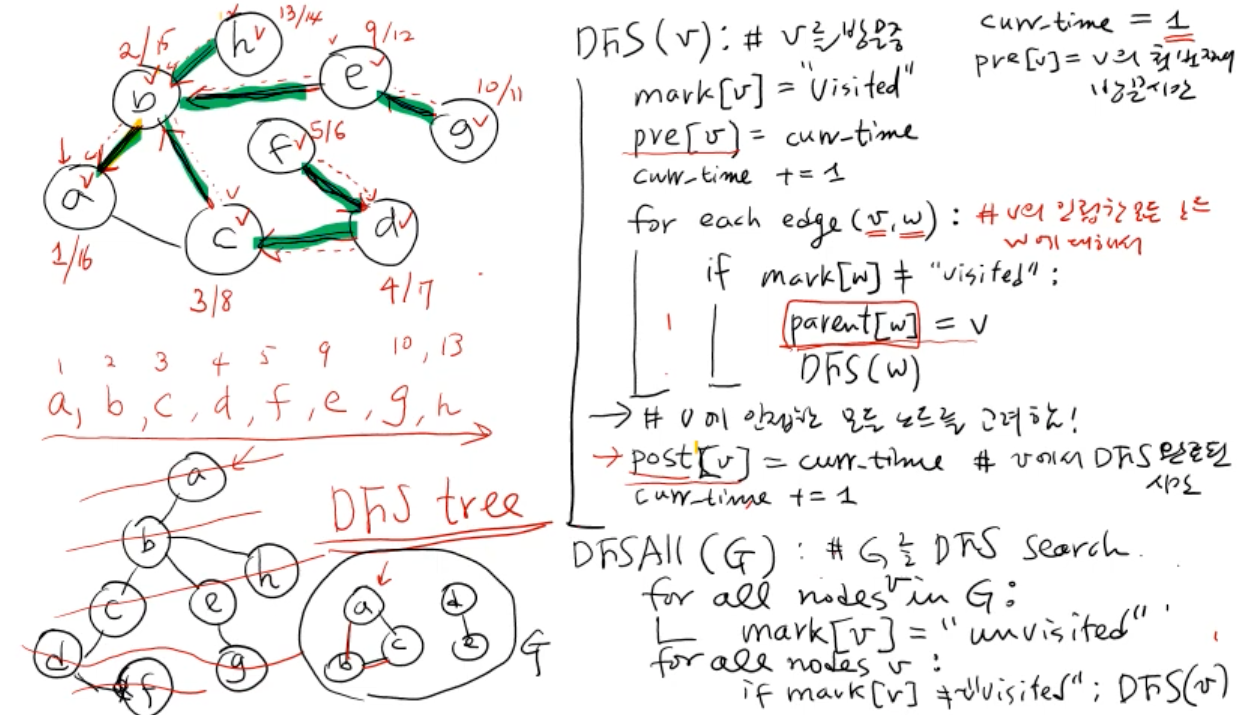
재귀적
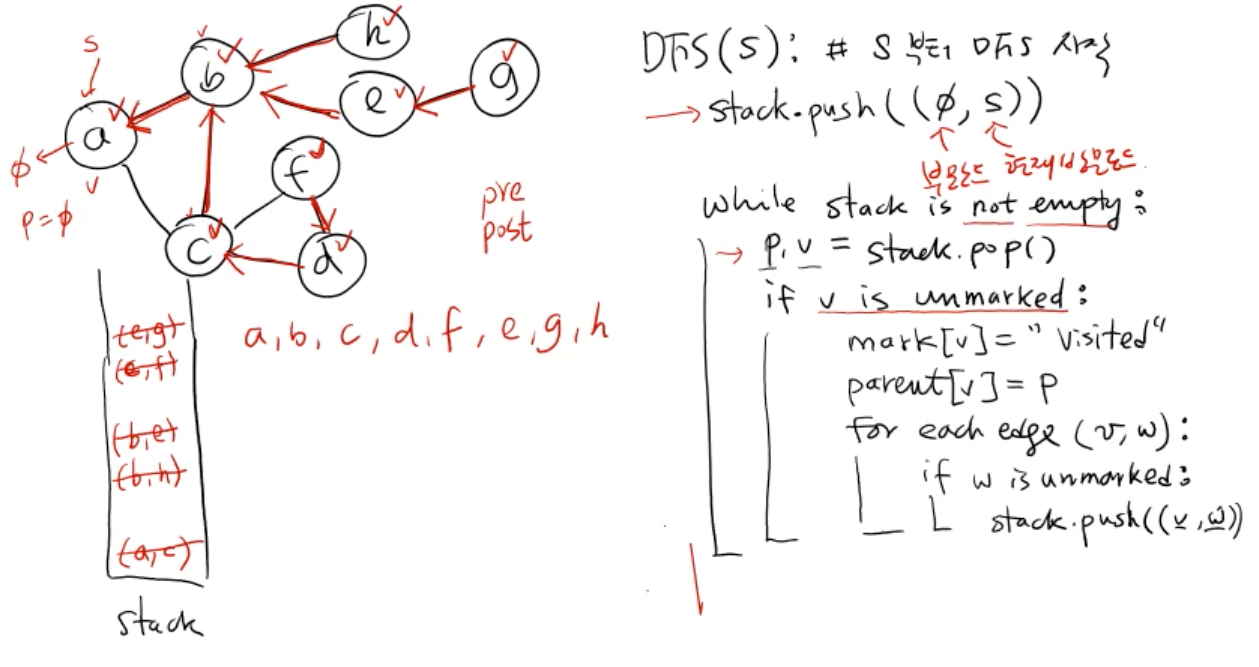
비재귀적
# 재귀적 dfs
def dfs(v): # v를 방문중
mark[v] = 'visited'
pre[v] = cur_time # v의 첫번째 방문시간
cur_time += 1
for each edge(v, w): # v의 인접한 모든 노드 w에 대해서
if mark[v] != 'visited':
# 저장된 parent 값을 가지고 DFS tree를 만들 수 있다.
parent[w] = v # 현재 방문 노드의 부모노드
dfs(w)
# v에 인접한 모든 노드를 고려했다.
post[v] = cur_time # v에서 dfs가 완료된 시간
cur_time += 1
return
# 비재귀적 dfs
def dfs(s):
stack.push((p, s)) # p: 부모노드, s: 현재 방문노드
while stack is not empty:
p, v = stack.pop()
if v is unmarked: # 해당 노드를 방문하지 않았다면
mark[v] = 'visited'
parent[v] = p
for each edge(v, w): # v에 인접한 노드에 대해서
if w is unmarked:
stack.push((v, w))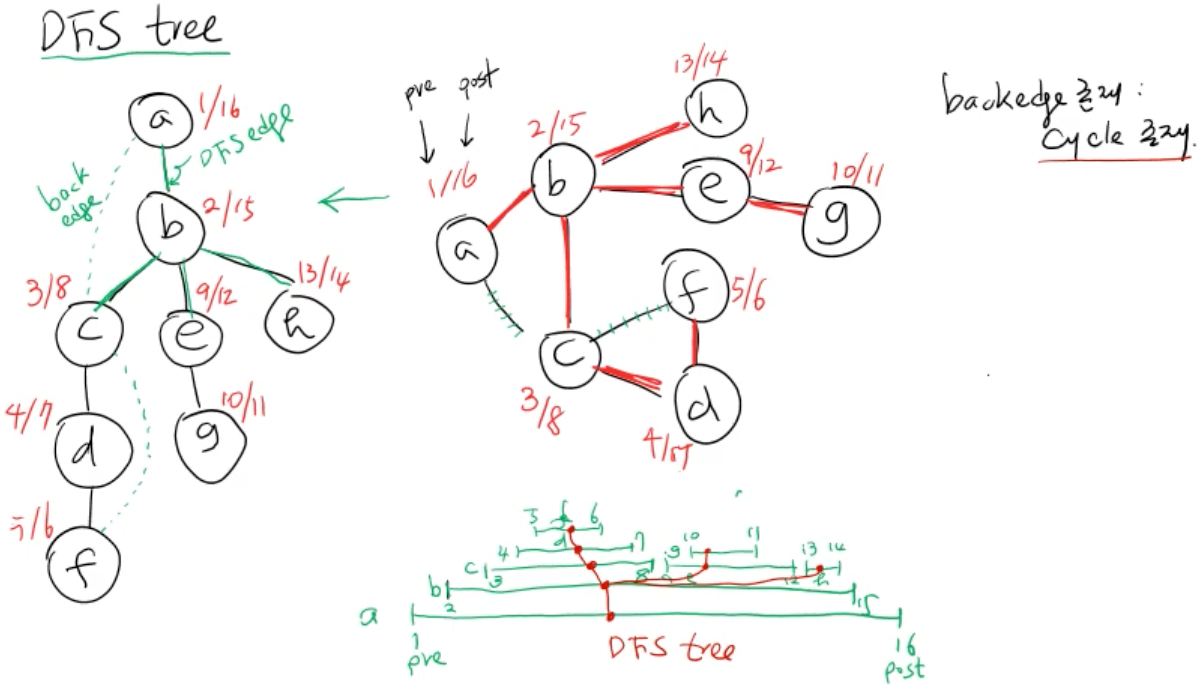
BFS (Breadth First Search)
특징
- 루트 노드나 임의의 노드에서 인접한 노드 (같은 레벨)를 모두 먼저 확인한 후 다음 level 탐색
- Queue를 사용한다.
DAG (Directed Acyclic Graph) 사이클이 없는 방향 그래프
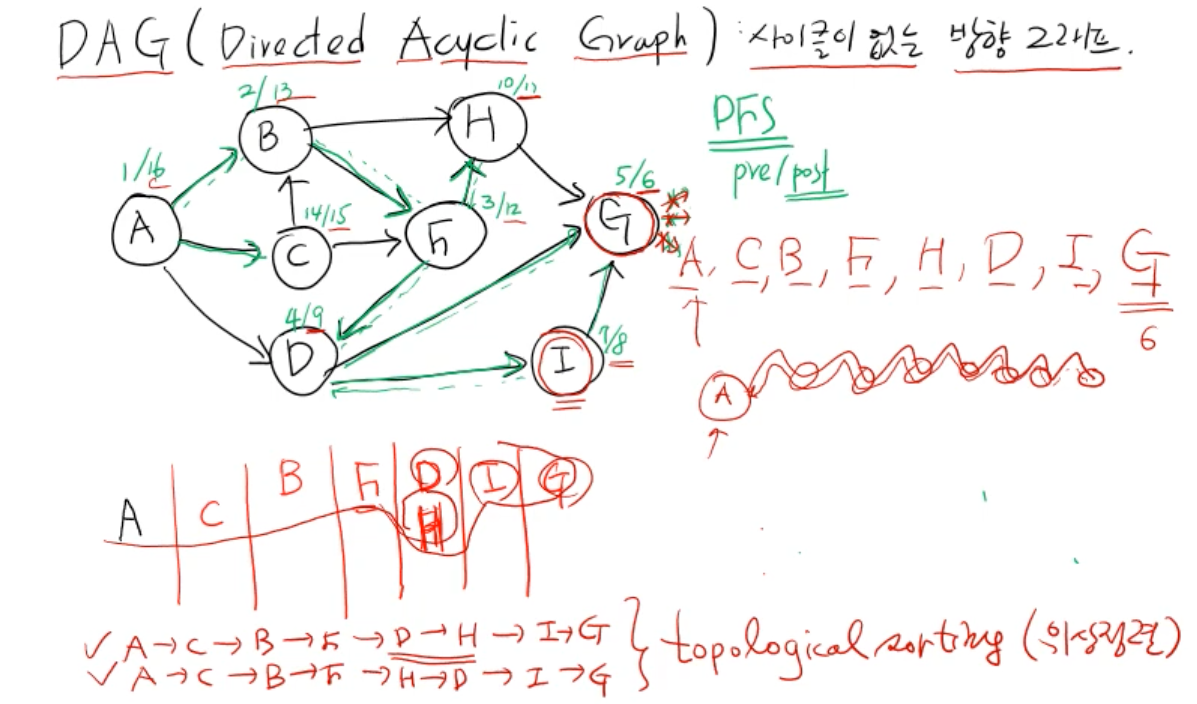
특징
- 선후관계에 따라 일의 순서가 여러가지 나올 수 있는데, 일의 순서를 결정하는 것을 위상정렬 (TopoLogicalSorting)
위상정렬
- DFS로 구현이 가능하다
- post_time의 가장 큰 순서로 나열하면 위상정렬이 된다.
