[Data Structure] Heap

힙 (Heap)

특징

• 모양성질 : 마지막 레벨을 제외한 노드가 다 차있고, 마지막 레벨에서 왼쪽부터 노드가 채워져 있을 경우
• heap property를 충족할 경우
  • 모든 부모노드의 key 값은 자식노드의 key값 보다 같거나 크다.

-> 힙(heap)이라고 할 수 있다.

• k번째의 노드의 인덱스

  • H[k]의 왼쪽 자식노드 = H[2 * k + 1], 오른쪽 자식노드 = H[ 2 * k + 2]
  • H[k]의 부모노드 = H[(k - 1) // 2]

• O(1)의 시간으로 부모, 자식노드를 알 수 있다.

• 제공연산
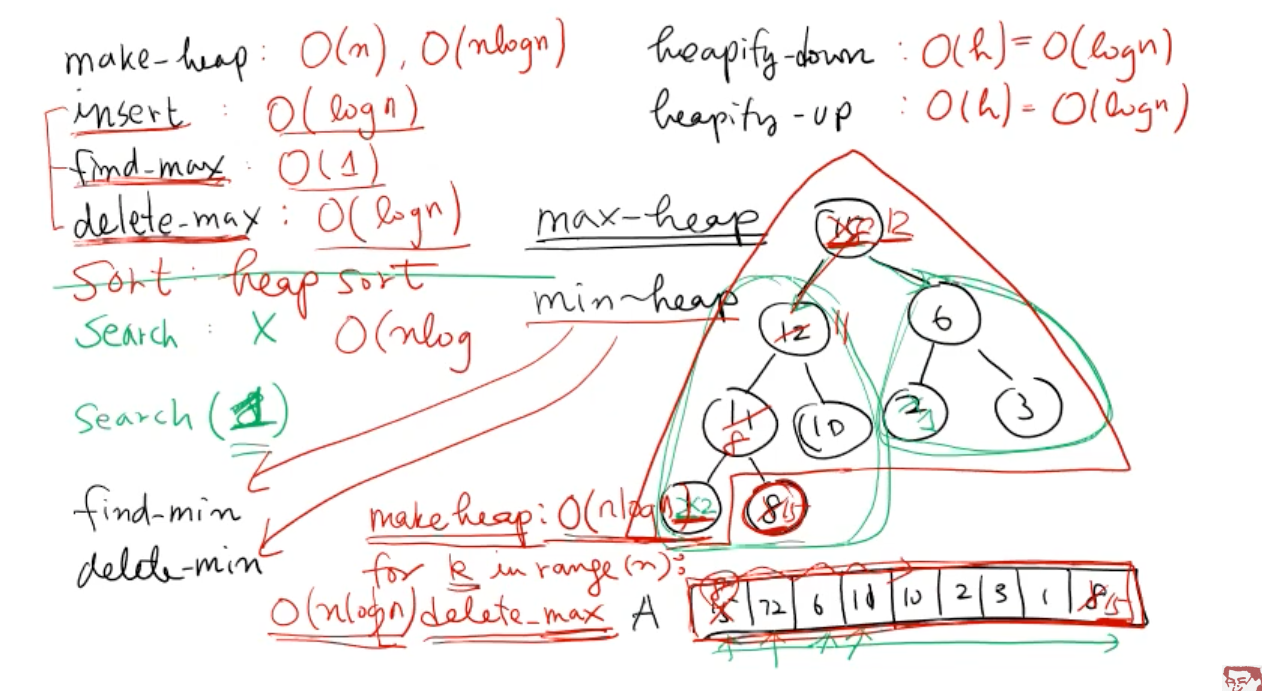
  • insert() O(log n)
  • find_max() : return list[0] O(1)
  • delete_max() O(log n)

heap_sort

from typing import MutableSequence
import random

def heapify(a: MutableSequence, left, right) -> None:
    largest = left
    cl = 2 * left + 1
    cr = 2 * left + 2
    if cl < right and a[cl] > a[largest]:
        largest = cl
    if cr < right and a[cr] > a[largest]:
        largest = cr
    if largest != left:
        a[largest], a[left] = a[left], a[largest]
        heapify(a, largest, right)
        
def heap_sort(a: MutableSequence) -> None:
    n = len(a)
    for i in range(n // 2, -1, -1): # 최대힙트리로 정렬
        heapify(a, i, n)
    for i in range(n - 1, -1, -1): # 최소힙트리로 정렬
        a[0], a[i] = a[i], a[0]
        heapify(a, 0, i)
    return a

if __name__ == '__main__':

    num = int(input())
    x = [None] * num
    for i in range(num):
        x[i] = random.randint(1, 100)
    heap_sort(x)
    print(x)

make_heap

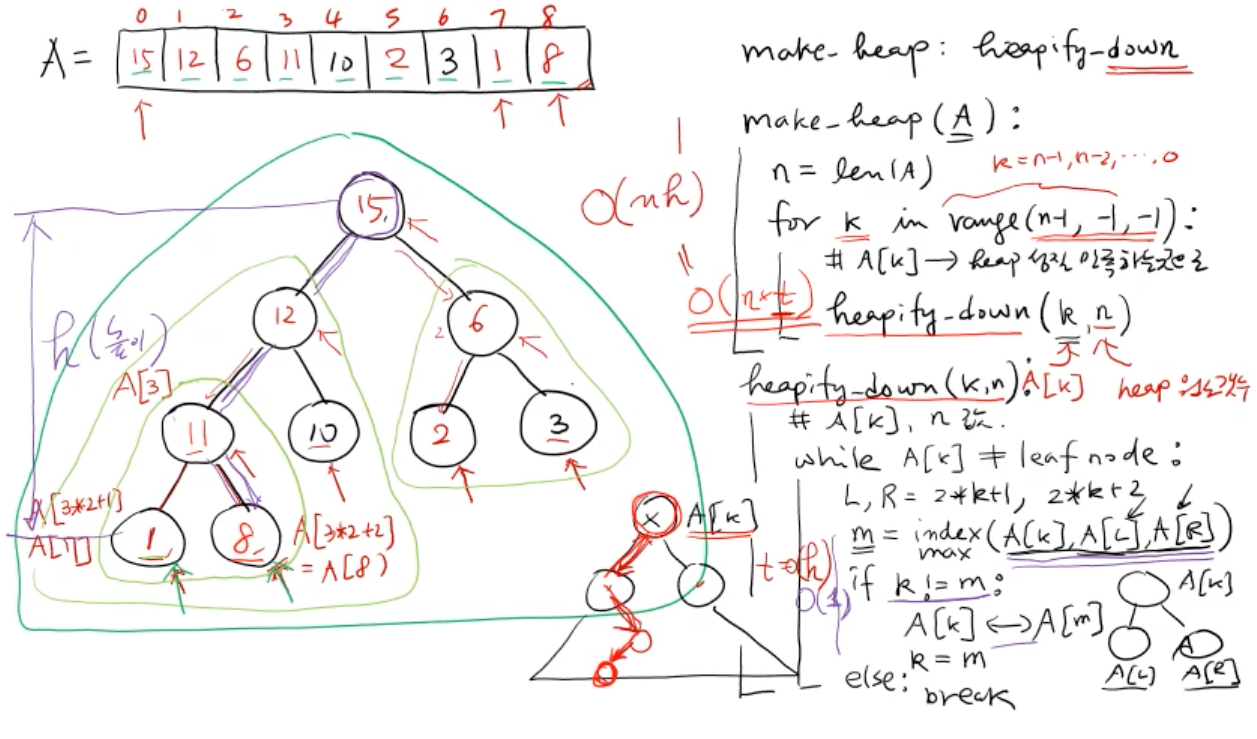
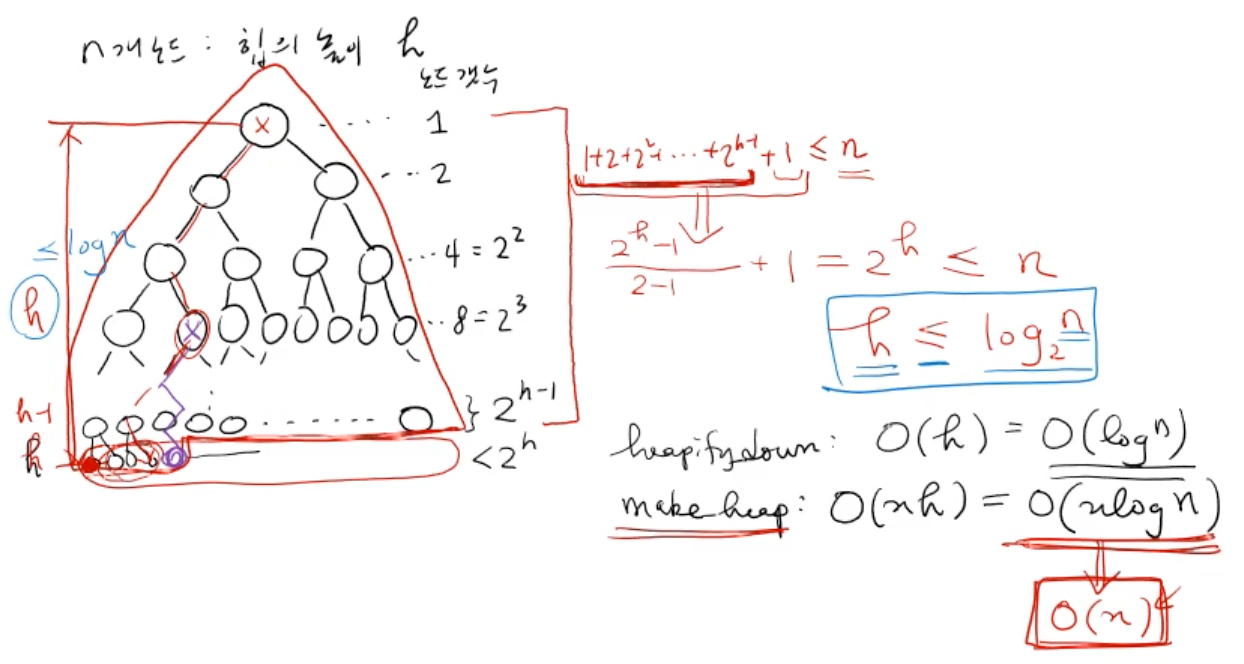
시간 복잡도 : O(nh) = 최악의 경우 O(nlogn)

루트에서 heapify를 할 경우 leaf노드까지 오래 걸리지만 leaf에 가까운 노드일 수록 더욱 짧게 걸린다

따라서, 실제로 수행시간은 O(nlogn) -> O(n)의 시간이 걸린다

insert

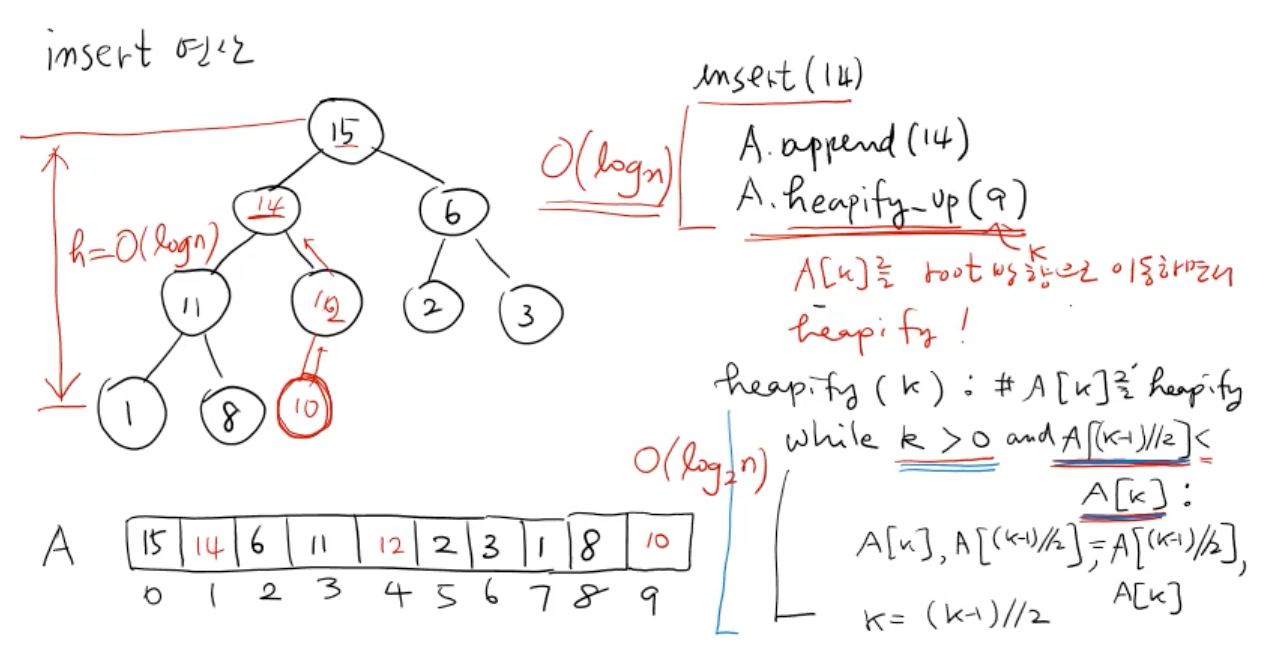
def insert(key): # 키 값
    A.append(key)
    A.heapify_up(i) # index
    # A[i]를 root방향으로 이동하면서 heap 성질을 만족하는지 판단
def heapify_up(i): # A[i]를 heapify
    while i > 0 and A[(i - 1) // 2] < A[i]:
    # index가 0보다 크고 A[i] (insert한 값)이 부모노드보다 클 때
    A[i], A[(i - 1) // 2] = A[(i - 1) // 2], A[i]
    i = (i - 1) // 2

n개의 숫자를 insert 하면 O(nlogn)
insert: O(logn), heapify_up: O(logn)
배열 A를 heap으로 만들고 싶으면
1. heap_sort로 O(n)시간을 통해 만들거나
2. insert로 O(nlogn)시간을 통해서 만들 수 있다.

find_max, delete_max

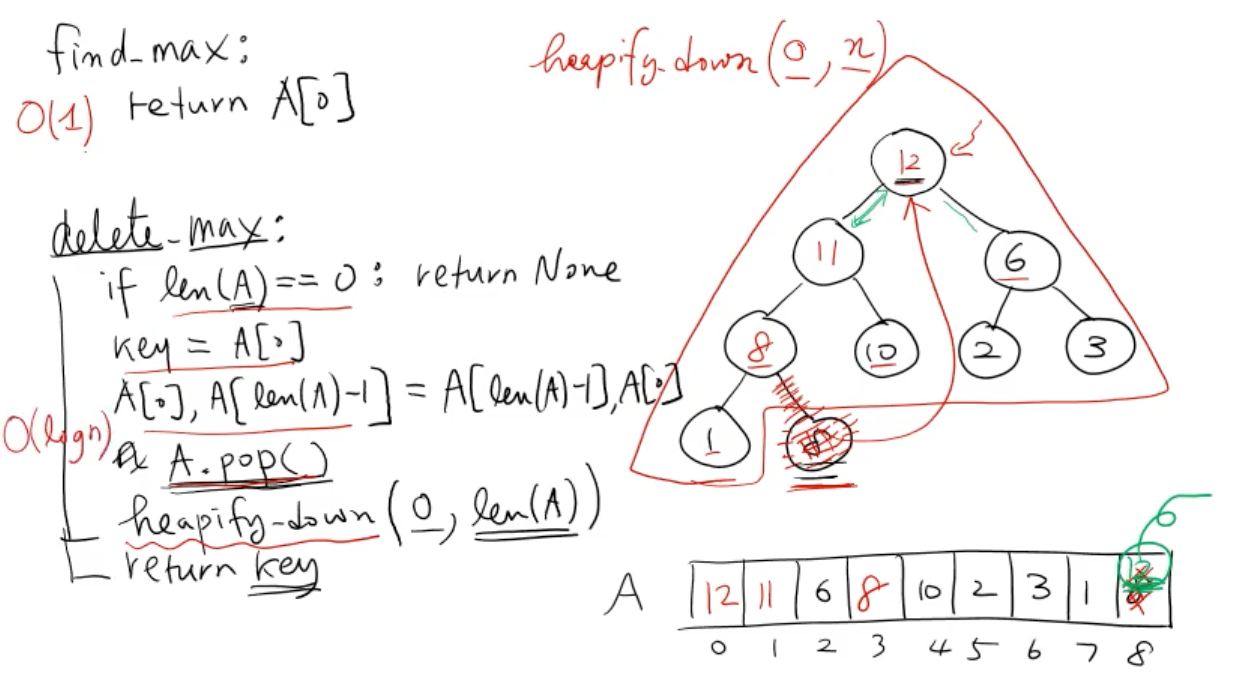
def find_max(A):
    return A[0]
    
def delete_max(A):
    if len(A) == 0: return None
    key = A[0]
    A[0], A[len(A) - 1] = A[len(A) - 1], A[0]
    A.pop()
    heapify(A, 0, len(A))
    return key

find_max: O(1), delete_max: O(logn)