Divide & Conquer

하... 실수로 작성했던 글이 날아가버렸...네요.

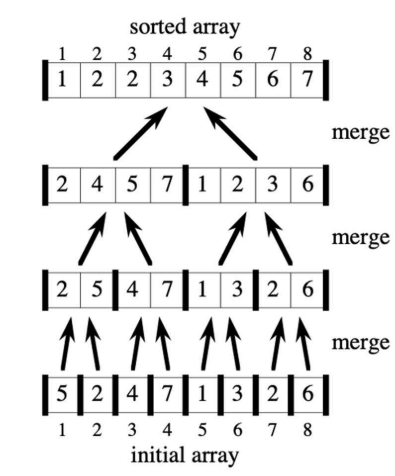
Merge sort에 대한 핵심적인 그림은 위와 같습니다. Sorting을 하는데 array를 원본그대로(in-place) sorting 하는게 아니라 작은 단위로 쪼개서 작은 array부터 sorting 하는 알고리즘이 바로 merge sort입니다.
Divide & conquer는 main problem을 recursively sub-problem으로 나눠서 sub-solution을 main problem의 solution에 활용하는 알고리즘을 의미합니다. 대표적으로 merge sort 알고리즘이 있고, merge sort를 통해 divide & conquer 알고리즘에 대해 살펴보도록 하겠습니다.

void merge_sort(std::vector<int>& vec, int start, int end)
{
  if(start < end)
  {
    int mid = (start + end) / 2;
    merge_sort(vec, start, mid);
    merge_sort(vec, mid+1, end);
    merge(vec, start, mid, end);
  }
}

• Divide
  - Main problem을 여러개의 sub-problem으로 나눈다.
  mid = (start + end) / 2;
• Conquer
  - Sub-problem의 사이즈가 충분히 작다면, sub-problem의 solution을 구한다.
  merge_sort(vec, start, mid);
merge_sort(vec, mid+1, end);
• Combine
  - Sub-solution을 main problem의 solution에 활용한다.
  merge(vec, start, mid, end);

merge(args)를 자세히 설명하면 아래와 같습니다.
함수는 start, mid, end pointer를 이용하여 start pointer value와 mid pointer value를 비교하여 increasing order로 sorting 하는 함수입니다. start pointer가 mid에 도달하거나 mid가 end에 도달하면 나머지는 copy하면 됩니다.

void merge(std::vector<int>& vec, int start, int mid, int end)
{
  static std::vector<int> sorted(MAX);
  int i = start;
  int j = mid + 1;
  int k = start;

  while(i <= mid && j <=end)
  {
    if(vec[i] <= vec[j])
    {
      sorted[k] = vec[i];
      i++;
    }
    else
    {
      sorted[k] = vec[j];
      j++;
    }
    k++;
  }

  if(i > mid)
  {
    for(int t = j; t <= end; t++)
    {
      sorted[k] = vec[t];
      k++;
    }
  }
  else
  {
    for(int t = i; t <= mid; t++)
    {
      sorted[k] = vec[t];
      k++;
    }
  }

  for(int t = start; t <= end; t++)
    vec[t] = sorted[t];

}

Time Complexity

Merge sort의 time complexity를 분석하면 다음과 같습니다.
$T(n)=\begin{cases} \Theta(1),\ if\ n=1 &\\2T(n/2) + \Theta(n)\ if\ n>1 \end{cases}$

Merge sort의 time complexity를 master method에 의해 단순하게 표현할 수 있고, 이는 아래와 같습니다.

$T(n)=\Theta(nlgn)$