Quick Sort

Quick sort는 배열을 분할하고, 각각의 부분 배열을 정렬하는 divide and conquer 방식의 정렬 알고리즘입니다. 이 알고리즘의 핵심은 pivot을 선택하는 것입니다. Pivot은 배열의 아이템 중 하나로 선택되며, 이를 기준으로 나머지 아이템을 분할합니다. pivot을 기준으로 배열을 분할한 후, 분할된 두 개의 부분 배열에서도 pivot을 선택하고 이를 기준으로 다시 분할합니다. 이 과정을 반복하며, 배열의 크기가 1이 될 때까지 분할합니다.

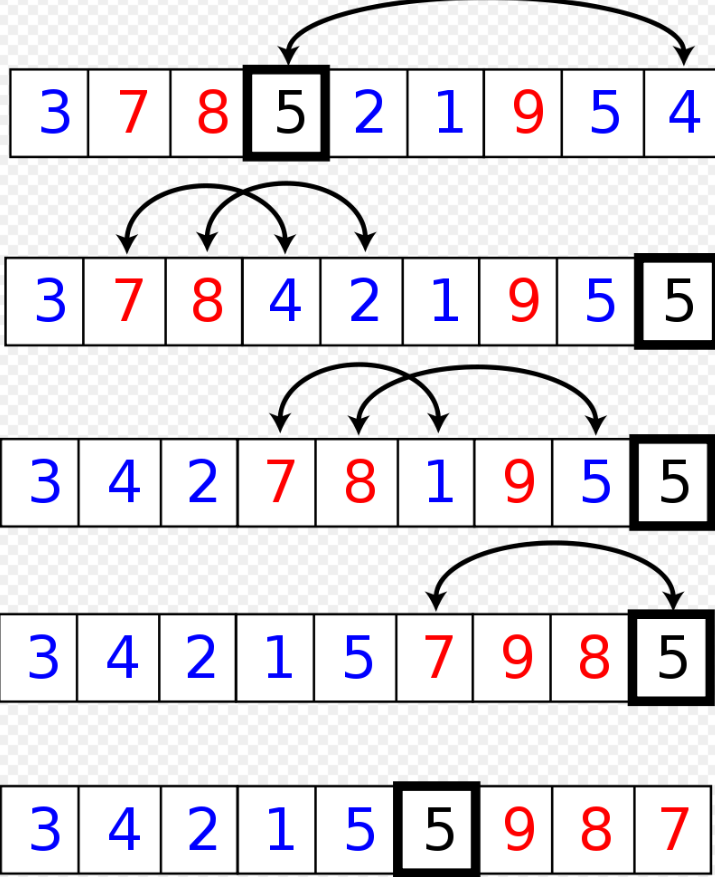[Quick sort - Wikipedia]

Quick Sort Algorithm

Quick sort algorithm은 아래와 같습니다.

do{
1. pivot을 선택합니다. 일반적으로 배열의 첫 번째 아이템을 pivot으로 선택합니다.
2. 배열을 pivot을 기준으로 분할합니다. pivot을 기준으로 왼쪽에는 pivot보다 작은 아이템이 오고, 오른쪽에는 pivot보다 큰 아이템이 옵니다.
3. 분할된 부분 배열에서도 pivot을 선택하고, 2번 과정을 반복합니다.
}while(Divide until leaf)

분할이 완료되면, 분할된 배열들을 합치고 정렬된 배열을 반환합니다.

Implementation

Quick sort 알고리즘의 구현부를 살펴보면 아래와 같습니다.

template <class T>
void QuickSort(T *a, const int left, const int right) {
	//a[left:right]를 비감소 순으로 정렬한다.
	//a[left]는 피벗으로 임의로 선정한다. 변수 i와 j는
	//서브리스트를 분할하는데 사용되어 항상 a[m] < pivot, m<i와
	//a[m] >= pivot, m>j를 만족시킨다. a[left] <= a[right+1]이라고 가정한다.
	if (left < right) {
		int i = left;
		int j = right + 1;
		int pivot = a[left];
		do {//계속하시오
			do i++; while (a[i] < pivot);
			do j--; while (a[j] > pivot);
			if (i < j) swap(a[i], a[j]);//이상한 놈들을 맞교환
		} while (i < j);//i<j이면
		swap(a[left], a[j]);//피봇을 알맞은 위치로 보냄
		QuickSort(a, left, j - 1);
		QuickSort(a, j + 1, right);
	}
}

Sorting problem을 pivot을 기준으로 divede & conquer를 수행하면서, QuickSort를 recursive call하는 방식으로 동작합니다.
pivot을 선정하는 과정이 pivot = a[left]에서 수행합니다.
pivot을 기주능로 sub-array의 element를 비교하여 std::swap을 수행하도록 구현되어 있습니다.
상기 QuickSort를 사용하는 예제 프로그램은 아래와 같습니다.

int main() {
	int R[10] = { 26, 5, 37, 1, 61, 11, 59, 15, 48, 19 };
	QuickSort(R, 0, 9);
	for (int i = 0; i < 10; i++)
		cout << R[i] << " ";
	cout << endl;
}

Complexity Analysis

Quick sort는 평균적으로 $O(nlgn)$의 시간 복잡도를 가지며, worst case에서는 $O(n^2)$의 시간 복잡도를 가집니다. Worst case는 pivot value를 계속해서 maximum/minimum value로 선정하는 경우에 해당합니다. Worst case를 피하기위해서 pivot을 적절히 고르는 것이 중요하고, 이를 수행하기 위해서 pivot을 array에서 randomly select하도라도 selected element가 minimum/maximum value인지만 checking해도 worst case를 피할 수 있습니다. 복잡도를 수식으로 표현하면 다음과 같습니다.

$T(n)=O(nlgn)$