그래프(Graph)는 여러 개의 노드(Node)와 그 노드들을 연결하는 간선(Edge)으로 구성된 자료구조이다. 그래프는 현실 세계에서의 여러 현상을 표현할 수 있으며, 다양한 문제들을 그래프로 모델링하여 해결할 수 있다. 여기서는 그래프의 종류, 특징 및 장단점, 복잡도 등에 대해 설명해보고자 한다.
그래프의 종류
그래프는 크게 무방향 그래프(Undirected Graph)와 방향 그래프(Directed Graph)로 나눌 수 있다.
무방향 그래프는 각 노드들이 서로 연결되어 있는 상태를 나타내며, 간선에 방향이 없다. 즉, 간선이 A와 B를 연결하면 A에서 B로 가는 것 뿐만 아니라 B에서 A로 가는 것도 가능하다.
방향 그래프는 간선에 방향성이 있는 그래프이다. A와 B를 연결한 간선이 A에서 B로 가는 방향으로만 갈 수 있는 것이다.
또한 가중 그래프(Weighted Graph)와 비가중 그래프(Unweighted Graph)로도 나눌 수 있다. 가중 그래프는 간선에 가중치(Weight)가 있는 그래프를 말하며, 각 간선이 어떤 의미를 가지고 있는지를 나타낼 때 사용한다.
무방향 그래프 (Undirected Graph)
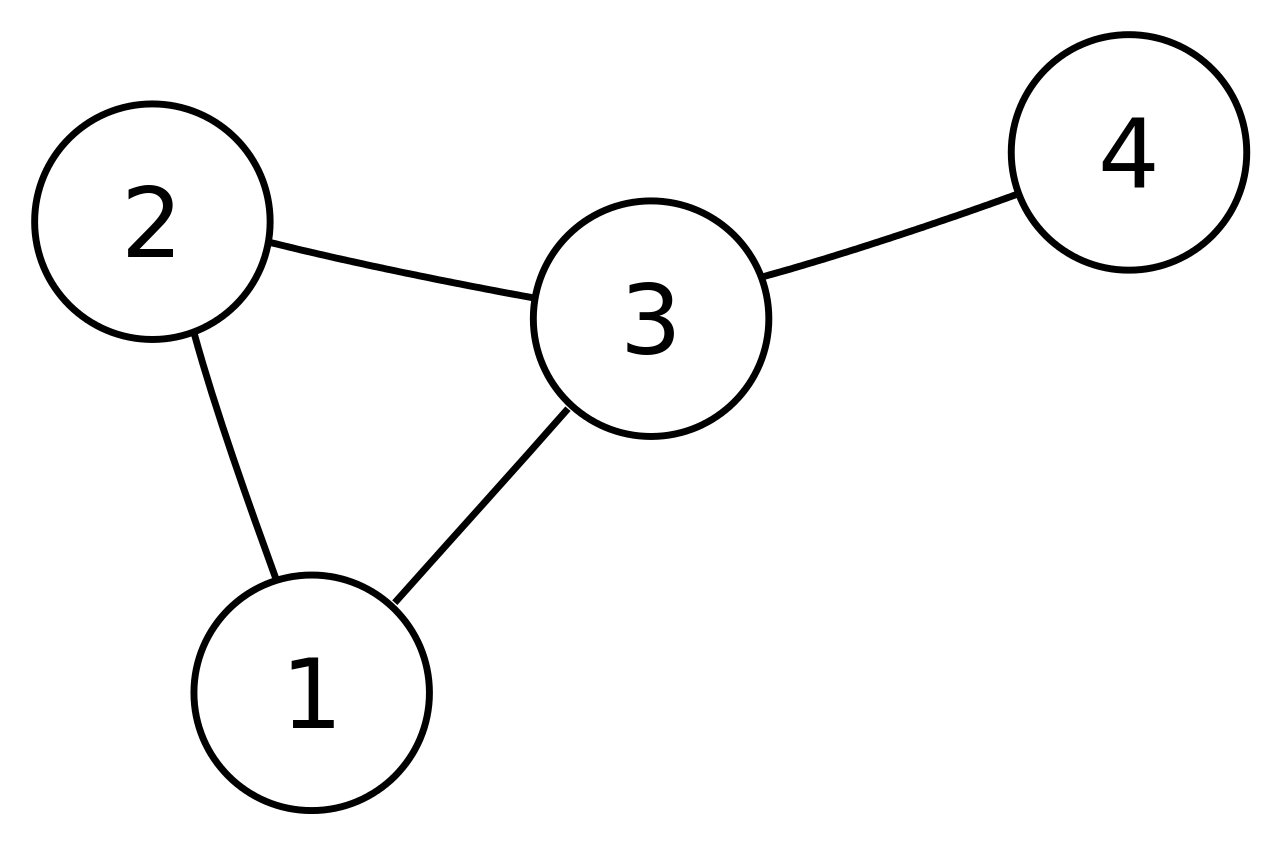
Undirected graph(무방향 그래프)는 간선의 방향성이 없는 그래프를 말합니다. 즉, 간선 (u,v)와 (v,u)는 동일한 간선으로 취급됩니다. 이러한 Undirected graph의 특징은 다음과 같습니다.
- 간선에 방향이 없기 때문에 인접한 두 정점은 서로에 대한 관계가 대칭적입니다.
- 양방향으로 갈 수 있는 도로, 지하철 노선도 등에 유용하게 쓰입니다.
- Edge의 개수가 많은 경우 더 복잡한 구조를 가질 수 있습니다.
하지만, Undirected graph의 단점은 다음과 같습니다.
- 방향이 없기 때문에 표현할 수 있는 정보가 제한적입니다. (예: 의존성 분석 등에서 사용하기 어려울 수 있습니다.)
- 경로 탐색에서 최적의 경로를 찾기 어렵습니다.
복잡도면에서, Undirected graph의 인접 리스트(Adjacency List)는 정점과 간선의 수를 V와 E라고 할 때, 공간 복잡도는 O(V+E)이며, DFS나 BFS와 같은 탐색 알고리즘의 시간 복잡도는 O(V+E)입니다.
방향 그래프 (Directed Graph)
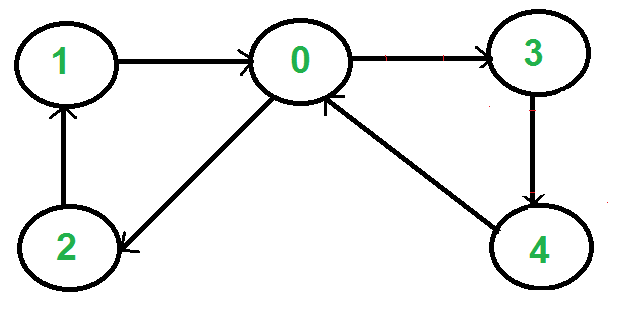
Directed graph, 즉 방향 그래프란 모든 에지에 방향이 있는 그래프를 말합니다. 즉, 에지가 (u,v)인 경우, 노드 u에서 노드 v로 가는 방향이 정해져 있습니다.
Directed graph의 특징은 다음과 같습니다.
- 에지의 방향성 때문에, u에서 v로 가는 경로와 v에서 u로 가는 경로가 다를 수 있습니다.
- 자기 자신으로 돌아오는 에지가 존재할 수 있습니다.
Directed graph의 장단점은 다음과 같습니다.
장점:
- 실제로 일어난 방향성을 반영할 수 있습니다. 예를 들어, 물류나 교통망 등에서 발생하는 방향성을 표현할 수 있습니다.
- 정보 전달, 네트워크 등에 적합합니다. 예를 들어, 전화 통화 기록이나 SNS 등에서 친구 관계를 나타낼 수 있습니다.
단점:
- 양방향 경로를 구현하기가 어렵습니다.
- 경로 탐색 등에 있어서 일방향 경로만 허용되기 때문에, 연산의 제약이 따릅니다.
Directed graph의 시간 복잡도는 그래프의 크기와 밀접하게 연관됩니다. 일반적으로 그래프는 노드 수와 에지 수를 고려하여 O(V+E)로 표기됩니다. 하지만 directed graph에서는 각 노드의 진입차수와 진출차수를 고려해야 합니다. 따라서 그래프의 크기와 진입/진출 차수의 분포에 따라 알고리즘 복잡도가 달라집니다.
가중치 그래프 (Weighted Graph)
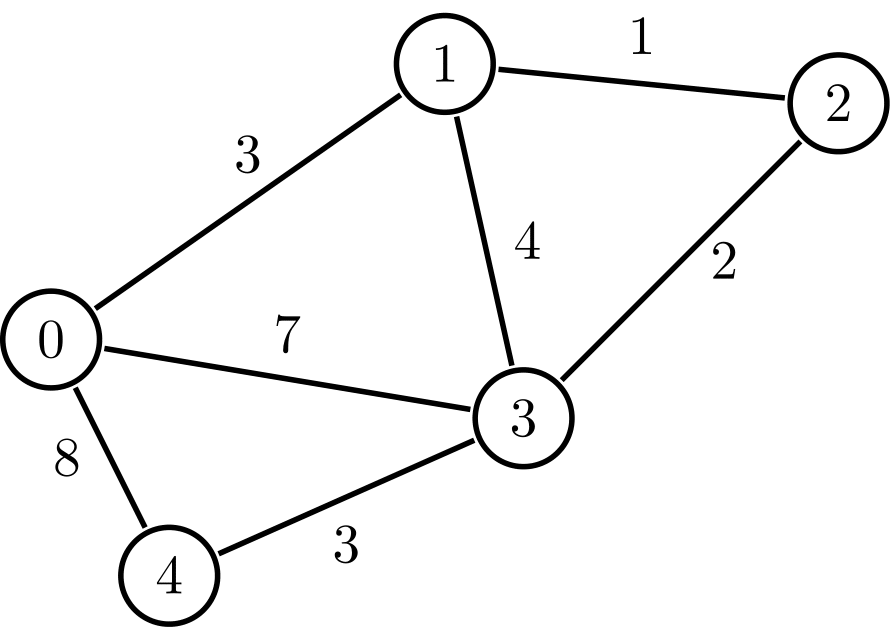
가중치 그래프는 간선에 가중치(weight)가 있는 그래프를 말합니다. 가중치는 간선의 비용이나 거리를 나타내는 값으로 사용됩니다.
Weighted Graph(가중 그래프)는 그래프의 각 에지(edge)에 가중치(weight)가 할당된 그래프를 말합니다. 가중치는 각 에지의 비용, 거리, 시간, 우선순위 등을 나타낼 수 있습니다.
Weighted Graph의 특징은 다음과 같습니다.
- 에지에 가중치가 할당되어 있으므로, 에지의 길이나 비용을 고려한 문제를 해결할 수 있습니다.
- 무방향 그래프와 방향 그래프 모두 가능합니다.
- 최단 경로 문제나 최소 스패닝 트리 문제 등의 문제를 해결할 수 있습니다.
Weighted Graph의 장단점은 다음과 같습니다.
장점:
- 가중치 정보를 포함하고 있기 때문에, 에지의 길이나 비용을 고려한 문제를 해결할 수 있습니다.
- 다양한 최적화 문제를 해결할 수 있습니다.
- 경로나 스패닝 트리 등을 찾는 문제에서 유용합니다.
단점:
- 그래프의 크기가 커지면 계산 비용이 매우 높아질 수 있습니다.
- 가중치가 음수인 경우에는 일부 알고리즘이 동작하지 않을 수 있습니다.
- Weighted Graph의 복잡도는 그래프의 크기(V)와 에지의 개수(E)에 따라 다릅니다. 대표적인 알고리즘인 최단 경로 알고리즘의 경우, 다익스트라 알고리즘과 벨만-포드 알고리즘의 시간 복잡도는 다음과 같습니다.
다익스트라 알고리즘: O((E+V)logV)
벨만-포드 알고리즘: O(VE)
이분 그래프 (Bipartite Graph)
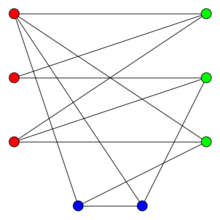
Bipartite Graph는 두 개의 그룹으로 나뉘어진 무방향 그래프로, 한 그룹에 속한 정점들끼리는 서로 인접하지 않으며 다른 그룹의 정점들과만 인접한다는 특징을 가지고 있습니다. 이러한 Bipartite Graph는 다양한 분야에서 활용되고 있습니다.
Bipartite Graph의 장점은 다음과 같습니다.
- 문제를 간단하게 해결할 수 있다: Bipartite Graph는 한 그룹의 정점들이 다른 그룹의 정점들과만 연결되므로, 그래프 내에서 최대 독립 집합과 최소 버텍스 커버 등의 문제를 쉽게 해결할 수 있습니다.
- 효율적인 연산이 가능하다: Bipartite Graph는 각 그룹 내에서는 서로 인접하지 않으므로, 이를 이용하여 행렬 계산 등의 연산을 효율적으로 수행할 수 있습니다.
Bipartite Graph의 단점은 다음과 같습니다.
- 현실 세계의 모든 문제를 모델링할 수 없다: Bipartite Graph는 한 그룹의 정점들과 다른 그룹의 정점들만을 연결할 수 있기 때문에, 그래프 내의 모든 정점들이 서로 연결될 수 없는 경우가 있습니다. 이 경우에는 다른 그래프 모델이 필요합니다.
- 양쪽 그룹의 크기가 일치해야 한다: Bipartite Graph는 두 그룹으로 나뉘어진 그래프이기 때문에, 양쪽 그룹의 크기가 일치해야 합니다. 만약 크기가 일치하지 않으면 Bipartite Graph로 모델링할 수 없습니다.
Bipartite Graph의 시간 복잡도는 일반적인 그래프와 같습니다. 즉, 인접 리스트로 구현한 경우 O(V+E), 인접 행렬로 구현한 경우 O(V^2)의 시간 복잡도를 가집니다.
완전 그래프 (Complete Graph)
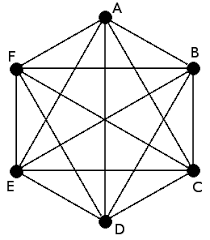
Complete Graph는 모든 정점들이 서로 연결된 그래프를 말합니다. 즉, n개의 정점이 있을 때, n(n-1)/2개의 간선을 가지는 그래프입니다. Complete Graph는 K(n)으로 표기합니다.
Complete Graph의 특징은 다음과 같습니다.
- 모든 정점들이 서로 연결되어 있어서, 경로나 연결성 문제를 해결하기 용이합니다.
- 경로나 거리가 최소가 되는 문제를 푸는 데 유용합니다.
- 전체 간선의 수가 많아지기 때문에, 구현하거나 계산할 때 시간 복잡도가 높아집니다.
Complete Graph의 장단점은 다음과 같습니다.
장점:
- 모든 노드가 서로 연결되어 있어서, 노드 간의 이동이 자유롭습니다.
- 경로나 거리가 최소가 되는 문제를 푸는 데 유용합니다.
- 노드가 많아도 구현하기 쉽습니다.
단점:
- 노드 간의 관계가 너무 밀접하기 때문에, 분석하기 어려울 수 있습니다.
- 노드가 많아질수록 연산 비용이 매우 높아집니다.
- 실제 상황에서 Complete Graph는 드물게 나타납니다. 대부분의 그래프는 부분 그래프(Partial Graph)입니다.
따라서, Complete Graph는 노드 수가 적거나, 모든 노드 간의 관계가 중요한 문제를 풀 때 유용하게 사용됩니다.
나무 그래프 (Tree Graph)
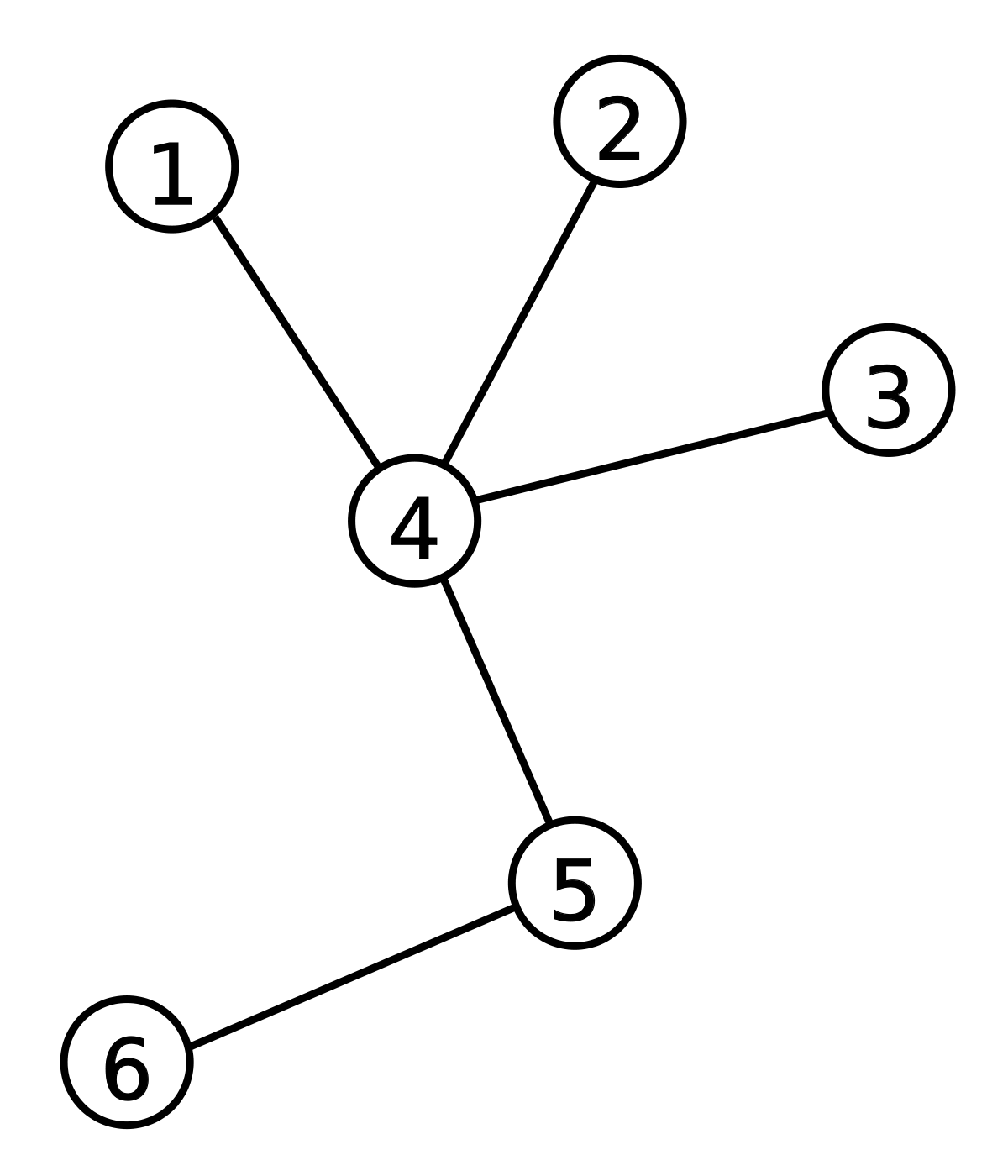
Tree Graph는 하나의 루트 노드에서 시작하여 여러 노드가 계층적으로 연결된 그래프입니다. 다음은 Tree Graph의 특징과 장단점에 대한 설명입니다.
특징:
- 하나의 루트 노드를 가지며, 각 노드는 하나의 부모 노드와 여러 개의 자식 노드를 가질 수 있습니다.
- 루트 노드에서 다른 모든 노드로의 경로는 유일합니다.
- 사이클이 없으며, 모든 노드가 연결되어 있습니다.
- 높은 계층의 노드에서 낮은 계층의 노드로의 연결만 가능합니다.
장점:
- 계층적인 구조로 데이터를 표현하기에 적합합니다.
- 루트 노드에서 시작하여 하위 노드로만 연결되기 때문에 검색이 빠르고 쉽습니다.
- 노드 간의 연결 정보만 저장하면 되므로, 저장 공간이 적습니다.
단점:
- 노드의 추가 및 삭제가 어려우며, 자식 노드가 많은 경우 검색 시간이 길어질 수 있습니다.
- 높이가 높은 편의 계층 구조를 가지므로, 노드의 개수가 많아질수록 높이가 커지고, 이는 성능 저하를 야기할 수 있습니다.
복잡도:
- 노드의 개수를 n, 에지의 개수를 m이라고 할 때, Tree Graph에서 노드와 에지를 모두 순회하는 시간 복잡도는 O(n+m)입니다.
- 특정 노드에서 다른 노드까지의 최단 경로를 찾는 경우, Breadth-First Search(BFS) 또는 Depth-First Search(DFS) 알고리즘을 사용할 수 있으며, 이 경우 시간 복잡도는 O(n+m)입니다.
그 외의 그래프
그 외에도 다양한 종류의 그래프가 존재합니다. 예를 들어, 계층 그래프(Hierarchical Graph)는 한 노드에서 다른 노드로 가는 경로가 하나뿐인 그래프를 말합니다. 네트워크 토폴로지(Network Topology)는 컴퓨터 네트워크에서 사용되는 그래프를 말합니다.
각 그래프의 특징과 장단점은 사용 목적에 따라 다르기 때문에, 그래프의 종류를 이해하고 각각의 특징을 파악하는 것이 중요합니다.
그래프의 관계
그래프의 포함관계는 일반적으로 다음과 같습니다.
트리는 그래프의 한 종류이며, 모든 트리는 그래프이지만 모든 그래프가 트리는 아닙니다.
무방향 그래프는 방향 그래프의 일종으로, 모든 무방향 그래프는 방향 그래프로 바꿀 수 있지만, 모든 방향 그래프가 무방향 그래프로 바뀔 수는 없습니다.
가중치 그래프와 비가중치 그래프는 각각 그래프의 한 종류이며, 어떤 그래프가 가중치 그래프이든지 비가중치 그래프이든지, 해당 그래프의 성질이 바뀌지는 않습니다.
