Red Black Tree

RB (Red-Black) Tree

Red-black tree(레드블랙 트리)는 self-balancing binary search tree(자가 균형 이진 탐색 트리) 중 하나입니다. Red-black tree는 자가 균형 이진 검색 트리의 일종으로, AVL 트리와 마찬가지로 트리의 균형을 유지하는 것이 주요 목적입니다. 이진 검색 트리의 일반적인 특징인 효율적인 탐색, 삽입 및 삭제를 보장하면서도, 트리의 균형을 유지함으로써 최악의 경우에도 O(log n) 시간 복잡도를 보장합니다. 각 노드는 레드 또는 블랙 색을 가지며, 다음과 같은 특징을 갖습니다.

1. 각 노드는 레드 또는 블랙 색을 가집니다.
2. 루트 노드는 블랙입니다.
3. 모든 리프 노드는 블랙입니다.
4. 레드 노드의 자식 노드는 모두 블랙입니다. (즉, 레드 노드는 연속해서 나타날 수 없습니다.)
5. 어떤 노드에서 리프 노드까지 경로 상에 있는 블랙 노드의 수는 모두 같습니다.

Red-black tree는 자체 균형 조정이 가능한 이진 탐색 트리입니다. 이 트리에서 삽입 및 삭제를 수행하는 데는 몇 가지 규칙이 적용됩니다.

먼저, 노드의 색상은 빨강 또는 검정 중 하나입니다. 이진 탐색 트리의 모든 노드는 검은색입니다.

다음은 삽입 및 삭제 알고리즘의 세부 사항입니다.

Insertion

Red-Black tree의 insertion에 대해 다루기 전에 rotate를 간단히 설명하겠습니다.
rotate는 argument로 입력되는 node를 기준으로 node간 pointer를 swap하여 node간 parent-child relation을 변경하는 것입니다.
아래 그림에 'Left-Rotate'와 'Right-Rotate'를 표현하였습니다.

[Tree에서 사용하는 rotate]

다음으로 레드 블랙 트리에 노드를 삽입하는 방법은 다음과 같습니다.

1. 삽입할 노드를 선택합니다.
2. 삽입할 노드를 이진 탐색 트리에 삽입합니다.
3. 삽입된 노드가 빨간색이면, 이중 빨간색 문제를 해결하기 위해 노드를 회전하거나 색상을 변경합니다.

이중 빨간색 문제는 Uncle node와 Red-Black tree의 property를 checking하는 current node(이하 'z')를 신경써야하는데, 이를 정리하면 아래와 같습니다.

1. 부모 노드가 루트 노드가 아닌 경우,
    - 부모 노드와 삼촌 노드를 확인합니다.
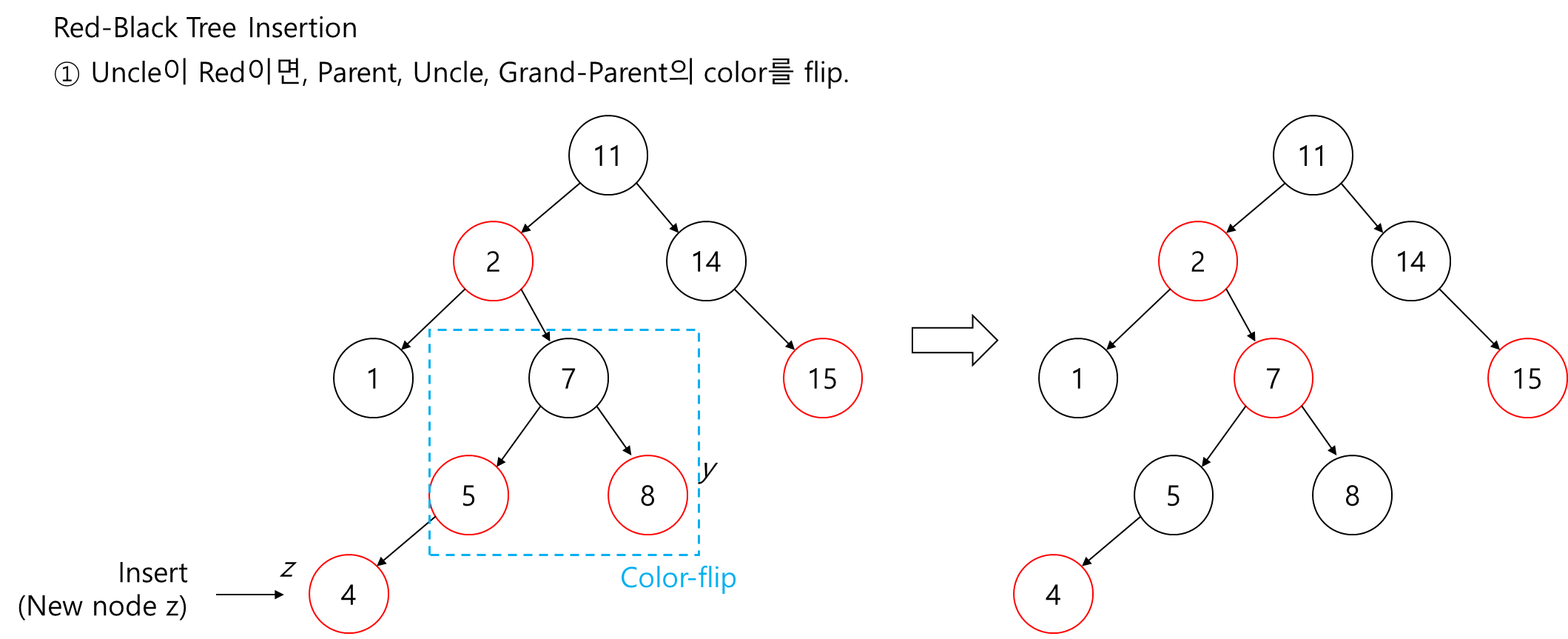
2. 삼촌 노드가 빨간색이면, 
    - 부모 노드와 삼촌 노드의 색을 변경하고 조부 노드의 색을 변경합니다.
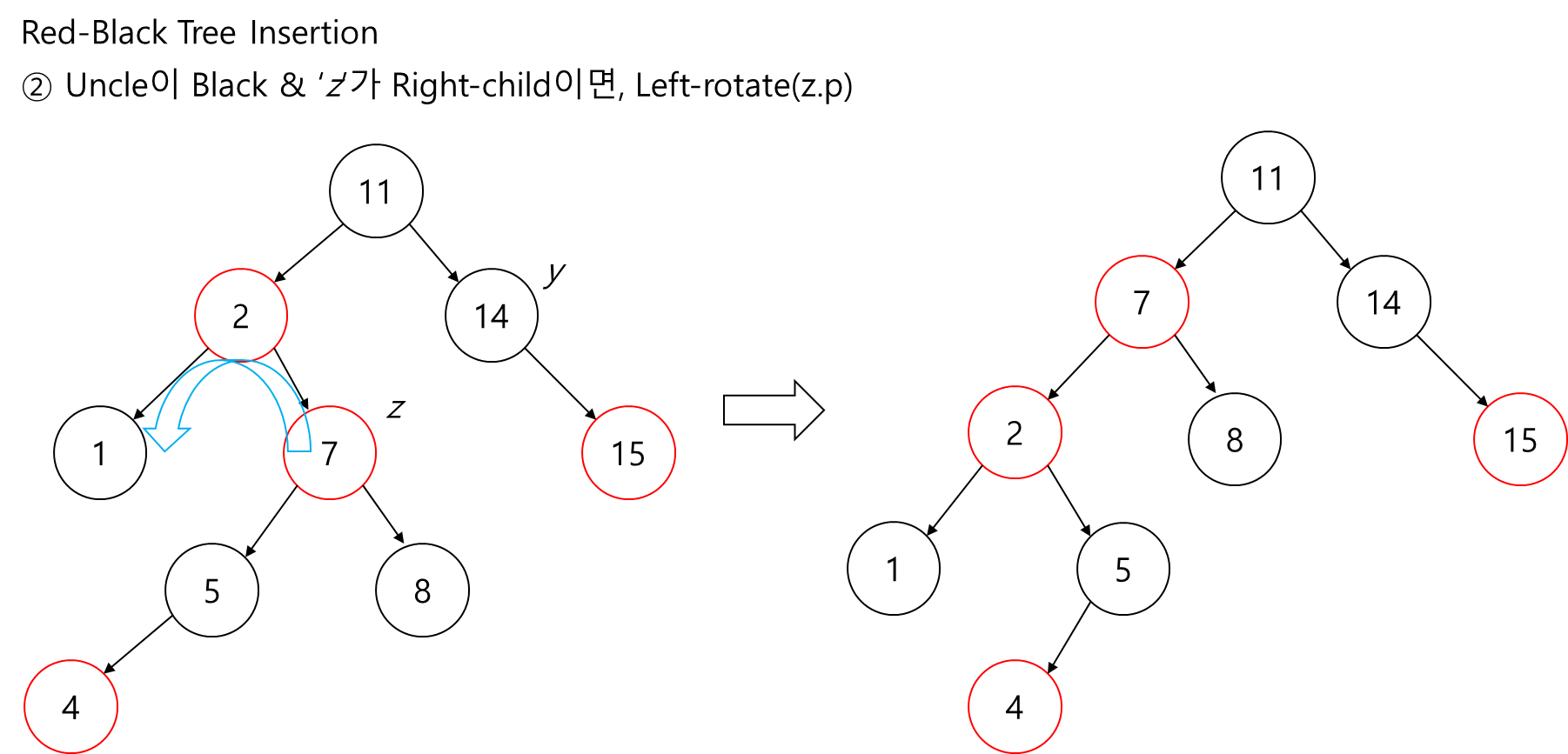
3. 삼촌 노드가 검은색이고 'z'가 right child이면, 
    - 'z'의 parent를 left-rotate.
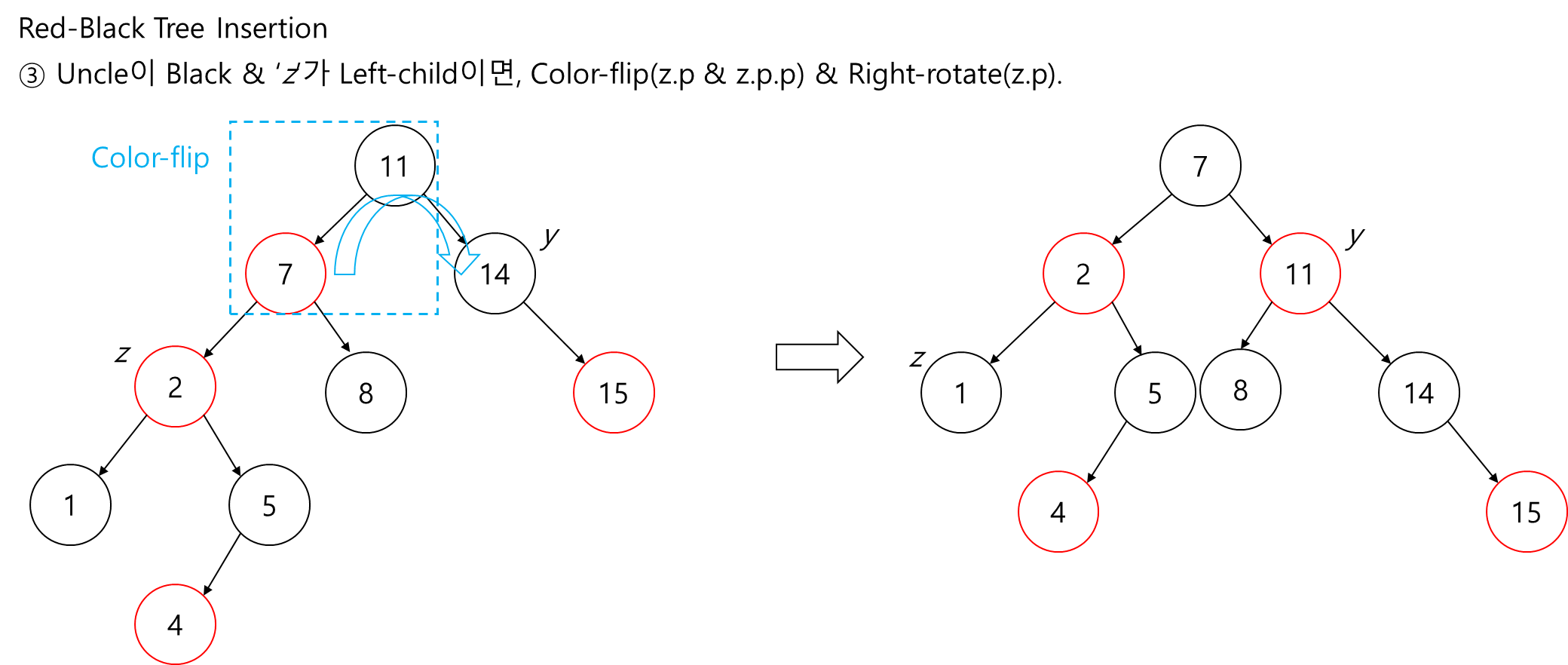
4. 삼촌 노드가 검은색이고 'z'가 left child이면, 
    - 부모 노드와 조부 노드의 색을 변경합니다. 
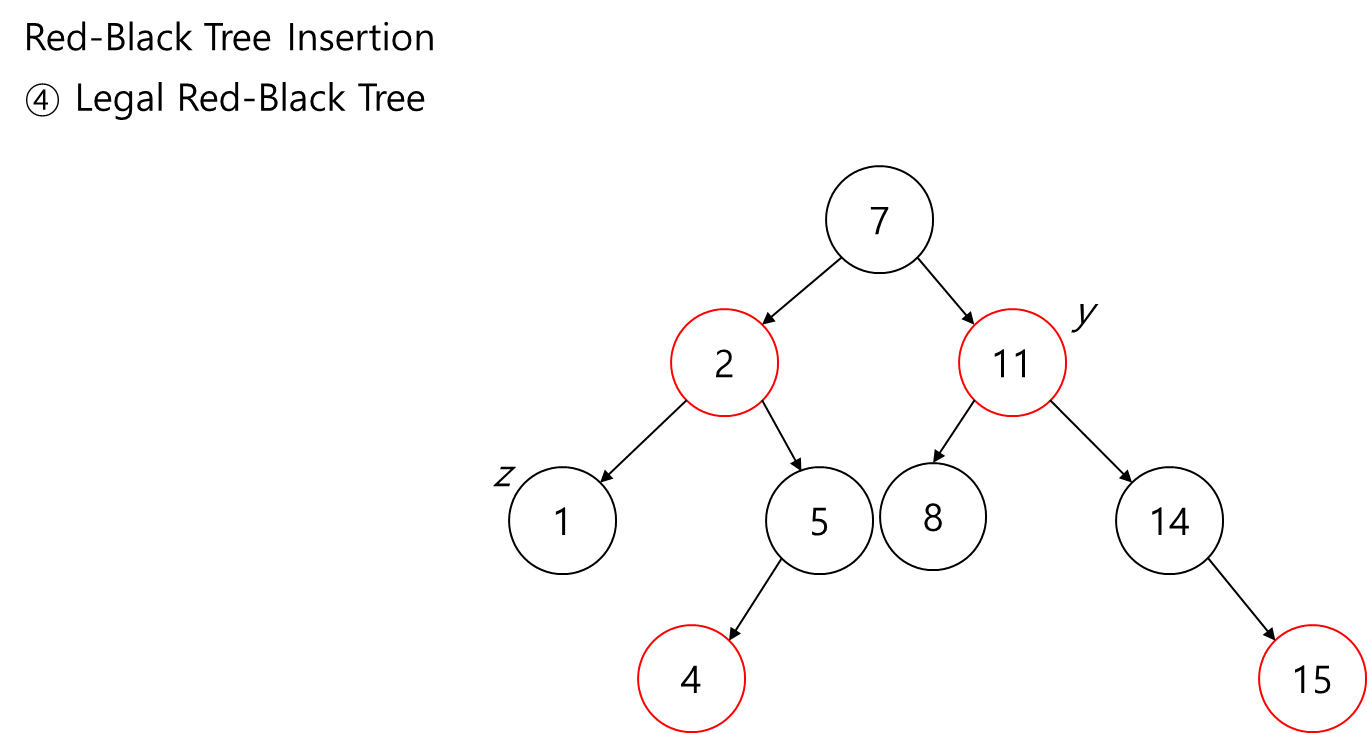
    - 'z'의 조부를 right-rotate.    

Red-Black tree의 insertion을 위의 case를 기준으로 분류하여 표현하면 아래의 그림과 같습니다.

Deletion

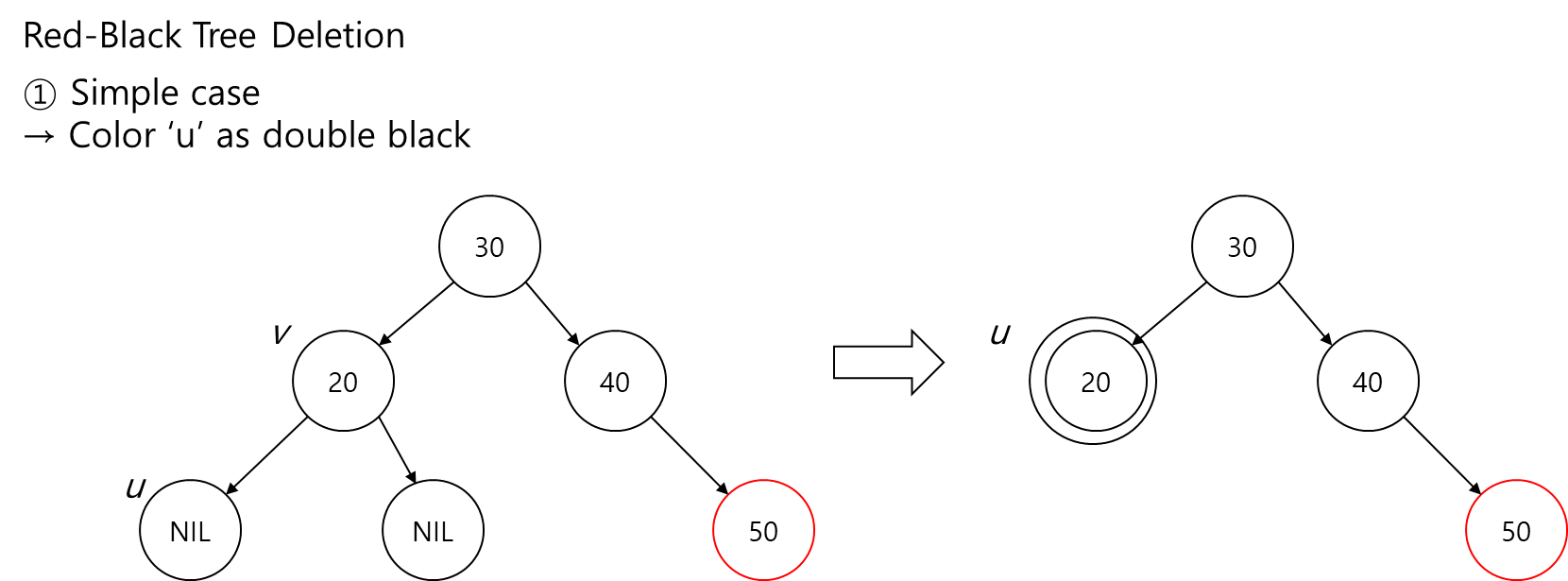
1. Delete node('v')가 leaf인 경우,
    - Current node만 삭제.
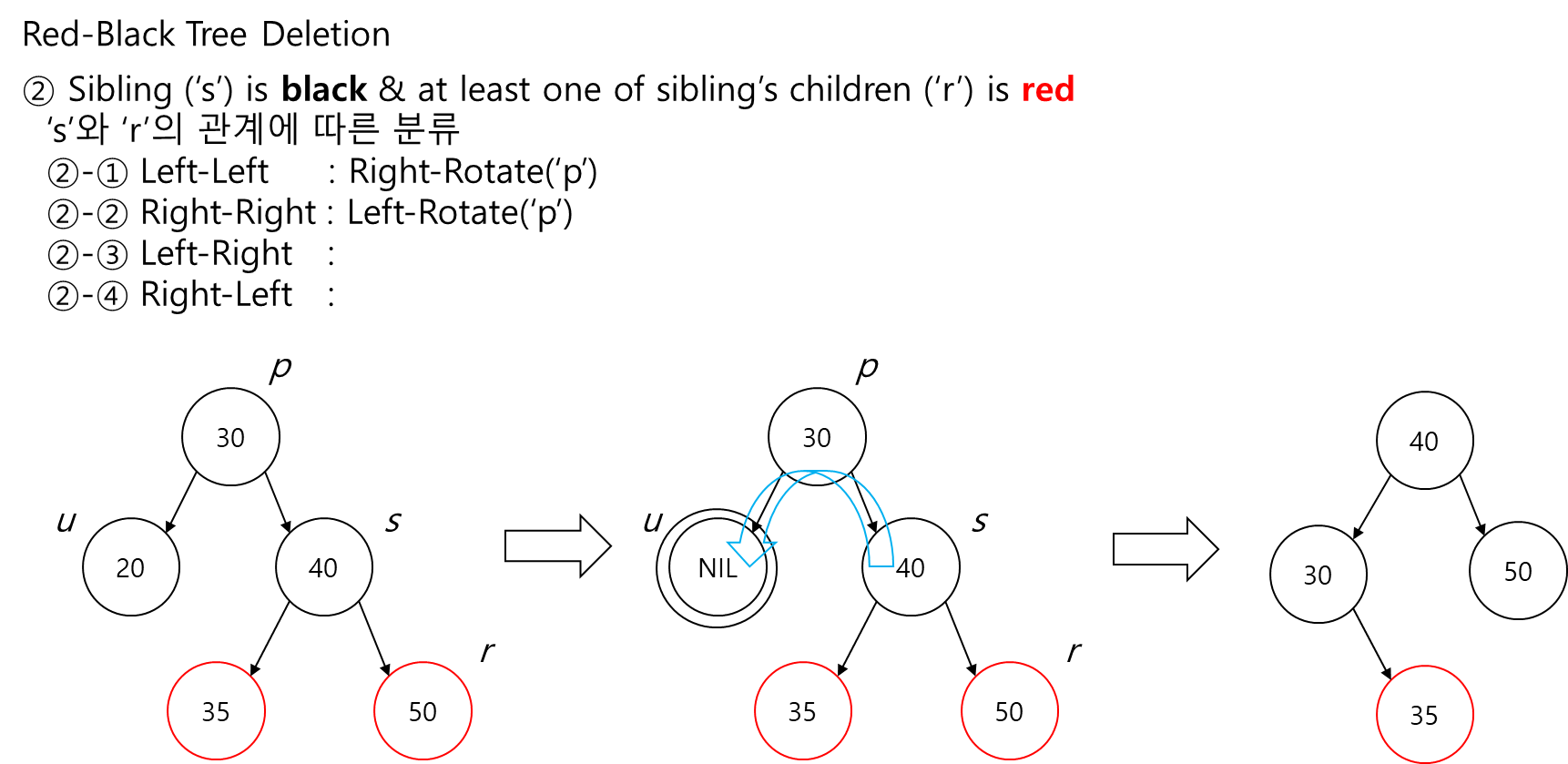
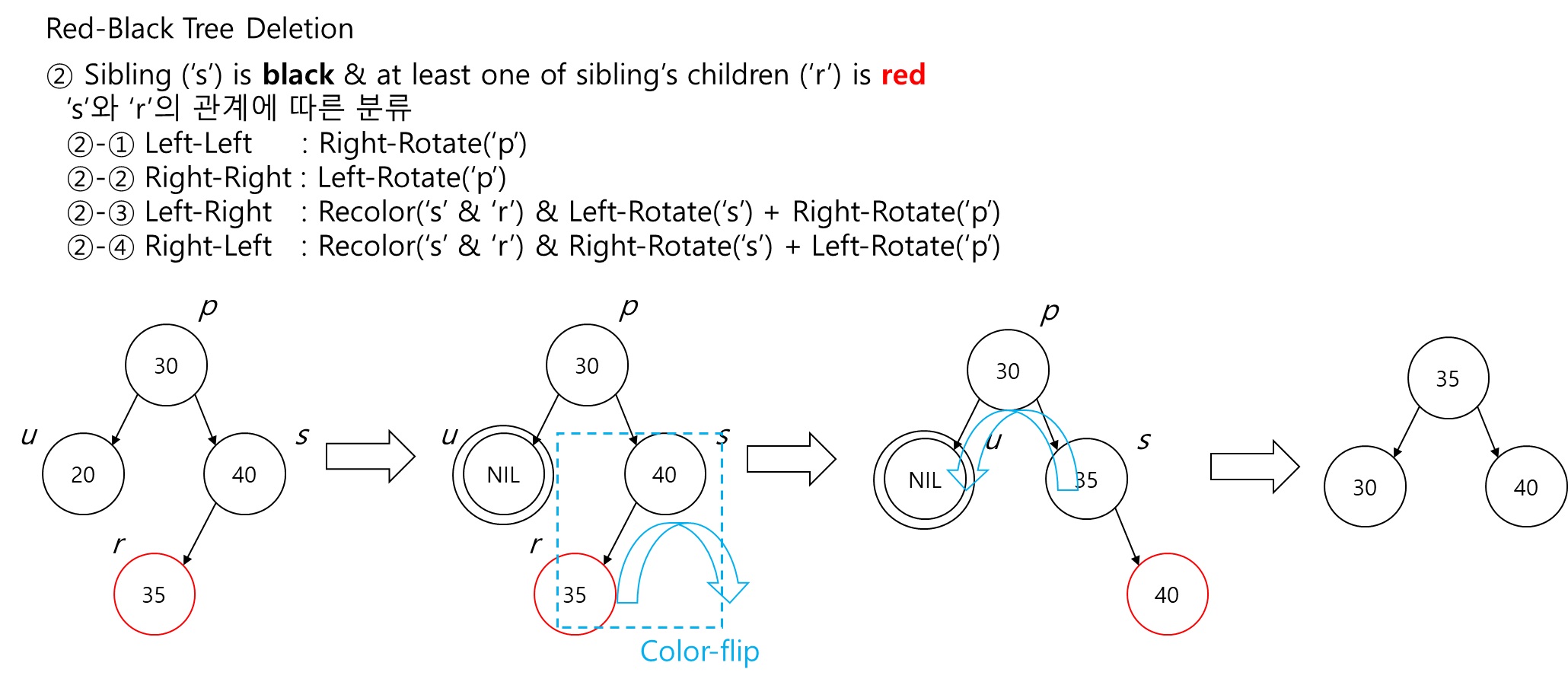
2. Sibling('s')이 black이고, sibiling의 children 중 하나가 red인 경우,
	- Sibling과 red child of sibling에 따라 sub-case가 나눠짐.
    - Symmetric case에 대해 반대되는 동작을 수행하면됨. (e.g., Left-Left ↔ Right-Right)
    - Right-Right: Left-Rotate('p'). (↔ Left-Left)
    - Right-Left: Recolor(‘s’ & ‘r’) & Right-Rotate(‘s’) + Left-Rotate(‘p’). (↔ Left-Right)
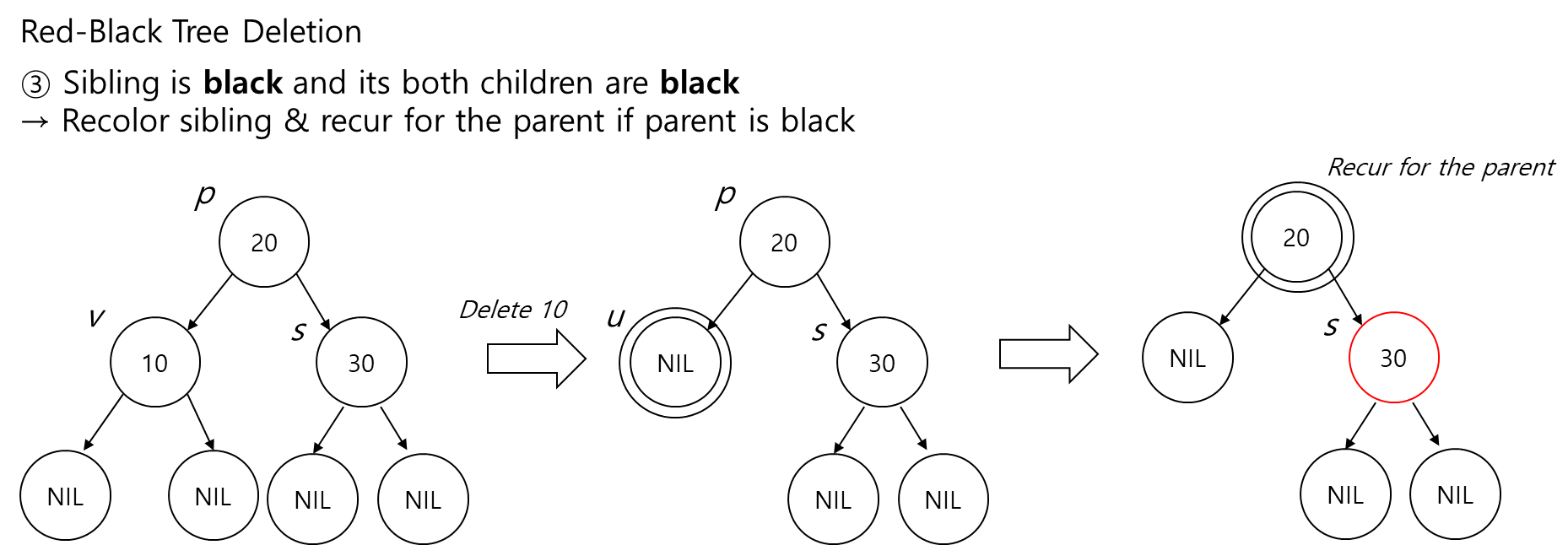
3. Sibling('s')이 black이고 sibling의 both children이 black인 경우,
	- Sibling을 recolor & parent에 대해 recur.
4. Sibling('s')이 red인 경우,
	- Sibling에 따라 sub-case가 나눠짐.
    - Right : Left-Rotate(‘p’) & Recolor(‘p’ & ‘s’) + Recolor(new ‘p’ & ‘s’) (↔ Left sibling)

Red-Black tree의 deletion을 위의 case를 기준으로 분류하여 표현하면 아래의 그림과 같습니다.

레드 블랙 트리는 균형이 잘 잡힌 이진 탐색 트리이므로, 삽입, 삭제, 검색 연산이 모두 O(log n) 시간에 수행할 수 있습니다.

이미지와 내용은 "Introduction to Algorithm 4th Edition"과 "https://www.geeksforgeeks.org/deletion-in-red-black-tree" 를 참고했습니다.
문의사항은 댓글로 남겨주세요~!