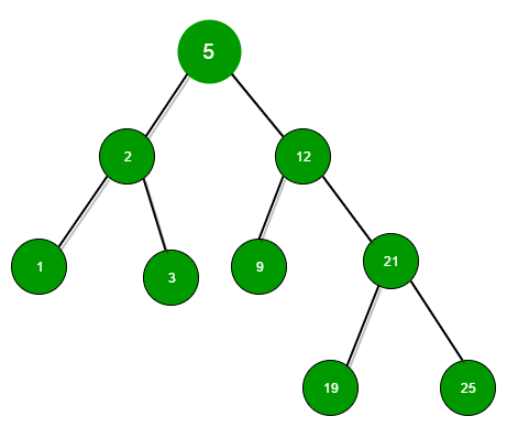
BST (Binary Search Tree)
Binary search tree(BST)는 이진 트리의 일종으로, 모든 노드가 최대 두 개의 자식 노드를 가지며, 왼쪽 자식 노드는 현재 노드보다 작은 값을, 오른쪽 자식 노드는 현재 노드보다 큰 값을 가지는 트리 자료구조이다. 이러한 특성으로 인해 탐색, 삽입, 삭제 등의 연산에 효율적으로 사용될 수 있다.
BST의 주요 특징은 다음과 같다.
- 이진 트리: 모든 노드가 최대 두 개의 자식 노드를 가지며, 자식 노드는 왼쪽과 오른쪽에 정해진 순서로 존재한다.
- 탐색 연산: 이진 탐색(Binary Search)의 원리를 적용해 탐색이 가능하다. 탐색 시 평균적으로 O(log n)의 시간 복잡도를 갖는다.
- 삽입과 삭제 연산: 탐색과 마찬가지로 O(log n)의 시간 복잡도를 갖는다. 또한, 삽입과 삭제 연산 후에도 이진 탐색 트리의 특성을 유지할 수 있도록 조치가 필요하다.
- 정렬된 상태 유지: BST는 특정한 값을 찾거나 정렬된 상태로 출력할 때 유용하게 사용될 수 있다.
하지만 BST의 단점도 존재한다.
- 편향된 트리: 삽입 순서에 따라 편향된 트리를 생성할 가능성이 있어 탐색 연산의 시간 복잡도가 O(n)으로 상승할 수 있다.
- 삭제 연산의 복잡도: 삭제 시 자식 노드의 위치에 따라 구현 방식이 달라질 수 있으며, 경우에 따라 구현이 복잡해질 수 있다.
- BST의 시간 복잡도는 일반적으로 O(log n)이지만, 최악의 경우(편향된 트리)에는 O(n)까지 상승할 수 있다.
BST는 주로 데이터를 정렬하거나, 탐색과 관련된 문제를 해결하는데 활용된다. 예를 들어, 디스크나 메모리 같은 저장장치에 데이터를 저장하고, 이를 검색하는 파일 시스템이나 데이터베이스 시스템에서 사용된다. 또한, 중위 순회(Inorder Traversal)를 사용해 정렬된 상태로 데이터를 출력할 수 있어 유용하게 활용된다.
BST Implementation Code
#include <iostream>
#include <queue>
using namespace std;
template<class K, class E>
struct Node{
Node(K ky, E el, Node<K, E> *left=0, Node<K, E> *right = 0)
: key(ky), element(el), leftChild(left), rightChild(right){}
Node<K,E> *leftChild;
K key;
E element;
Node<K, E> *rightChild;
int leftSize;
};
template<class K, class E>
class BST{
public:
BST(){root = 0;}
void Insert(K &newkey, E &el){Insert(root, newkey, el);}
void Preorder() {Preorder(root);}
void Inorder() {Inorder(root);}
void Postorder() {Postorder(root);}
void Levelorder();
bool Get(const K&, E&);
bool Print();
bool RankGet(int r, K &k, E &e);
void Delete(K &oldkey){Delete(root, oldkey);}
void ThreeWayJoin(BST<K, E>& small, K midkey, E midel, BST<K, E>& big);
void TwoWayJoin(BST<K, E>& small, BST<K, E>& big);
private: //helper 함수들
void Visit(Node<K, E> *);
void Insert(Node<K, E>* &, K &, E &);
void Preorder(Node<K, E> *);
void Inorder(Node<K, E> *);
void Postorder(Node<K, E> *);
void Delete(Node<K, E>* &, K &);
Node<K, E> *root;
};template <class K, class E>
void BST<K, E>::Insert(Node<K, E>* &ptr, K &newkey, E &el){//Insert의 helpler 함수
if(ptr==0) {ptr = new Node<K, E>(newkey, el); ptr->leftSize = 1;}//아무것도 없으면
else if(newkey < ptr->key) {ptr->leftSize++; Insert(ptr->leftChild, newkey, el);}
else if(newkey > ptr->key) Insert(ptr->rightChild, newkey, el);
else if(newkey == ptr->key) ptr->element = el;//같은 key가 있으면
else ptr->element = el;//Update element
}template <class K, class E>
void BST<K, E>::Delete(Node<K, E>* &ptr, K &oldkey){
Node<K, E>*tmpptr; Node<K, E> *tmpdaddyptr;
if(ptr == 0) return;//그런 노드가 없으면 그냥 return
if(oldkey < ptr->key) Delete(ptr->leftChild, oldkey);
else if(oldkey>ptr->key){//우측 아들을 루트로 하는 트리에서 지우시오
Delete(ptr->rightChild, oldkey);
}
else{//ptr노드가 바로 지울 노드인 경우임
if(!ptr->leftChild && !ptr->rightChild)//아들이 없다면
{delete ptr; ptr = 0; return;}
else if(ptr->leftChild && !ptr->rightChild)
//그 아들을 ptr가 가리키게 하고 현재 ptr가 가리키는 노드 지움
{ tmpptr = ptr; ptr = ptr->leftChild; delete tmpptr; return;}
else if(ptr->rightChild && !ptr->leftChild)
{ tmpptr = ptr; ptr = ptr->rightChild; delete tmpptr; return;}
else{//두 아들있음:루트가 rc인 우측트리에서 '제일 작은 노드'찾자
Node<K, E> *rc = ptr->rightChild;//rc가 루트인 subtree
if(!rc->leftChild)//rc가 왼쪽아들이 없으면 rc가 그 노드!
{ptr->key = rc->key; ptr->element = rc->element;
ptr->leftChild = rc->rightChild; delete rc;
}
else{
while(rc->leftChild){
rc = rc->leftChild;
}
ptr->key = rc->key; ptr->element = rc->element;
ptr->leftChild = rc->rightChild; delete rc;
}
}
}
}Traversal
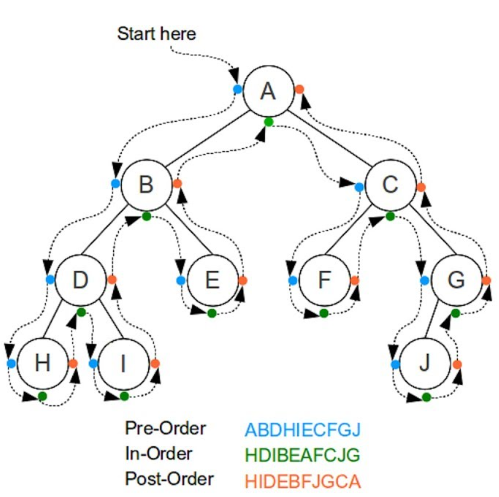
트리 자료구조에서 노드를 탐색하는 방법 중 세 가지인 전위 순회(pre-order traversal), 중위 순회(in-order traversal), 후위 순회(post-order traversal)에 대해 간단하게 설명해보겠습니다.
Pre-order Traversal
template <class K, class E>
void BST<K, E>::Preorder(Node<K, E> *currentNode){//Preorder의 helper 함수
if(currentNode){
Visit(currentNode);
Preorder(currentNode->leftChild);
Preorder(currentNode->rightChild);
}
}Post-order Traversal
template <class K, class E>
void BST<K, E>::Postorder(Node<K, E> *currentNode){
if(currentNode){
Postorder(currentNode->leftChild);
Postorder(currentNode->rightChild);
Visit(currentNode);
}
}In-order Traversal
template <class K, class E>
void BST<K, E>::Inorder(Node<K, E> *currentNode){
if(currentNode){
Inorder(currentNode->leftChild);
Visit(currentNode);
Inorder(currentNode->rightChild);
}
}