Velocity Vector
속도에 대해 다시 얘기해보자. 속도는 위치의 변화량이고, 이를 벡터를 이용해서 표현할 수 있다고 했다.
위치가 단위시간동안 계속 변할 때, 그 변화량이 바로 속도다. 속도는 크기와 방향을 갖고 있다. 이를 우리는 벡터로 표현할 수 있다.
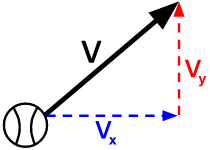
야구공이 어떤 물체의 위치이고, 이 위치에서 변화량이 바로 v가 된다. 이 v값이 바로 벡터라고 볼 수 있다. 위치의 변화량은 속도이므로 이 v가 그냥 속도를 의미하는 벡터가 되는 것이다.
보다시피 위치의 변화량은 x와 y값이 얼마나 증가했느냐다. 좌표계에서 이 x, y의 증가량을 벡터로 표현하면 일반적인 좌표의 개념과 같이 단순히 (x, y)로 표현된다.
문제는 이 (x, y)가 갖고 있는 의미가 위치가 아니라 변화량인 벡터를 뜻한다는 것이다. 원점에서 이 (x, y)를 가리키는 화살표를 그리고 그 각도가 바로 방향이 된다.
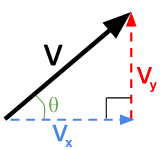
따라서 우리는 캔버스에서 어떤 물체를 움직이게 할 때, 해당 물체의 위치값에 속도벡터를 더해주기만 하면 된다.
이 때
- 이동거리는 얼마나 될 것인지?
- 그 방향은 어디인지?
이를 벡터로 정해줄 수 있다.
angle
어떤 물체 A를 90° 방향으로 움직인다고 하면, 캔버스 좌표계에서는 시계방향으로 각도가 증가하게 되므로, 6시 방향이 90°가 될 것이다.
90°는 라디안으로 π/2 이므로
const angle = Math.PI/2위와 같이 각도를 쉽게 나타낼 수 있다.
그렇다면 90°를 나타내는 벡터를 하나 정의해보자. 벡터는 (x, y)값으로 표현되는데, 이 값에 각도를 어떻게 정해줄까?
간단하다. 직관적으로, 90° 방향에 있는 벡터를 하나 나타내기만 하면 된다. 이 벡터는 y축 위에 있을 것이므로 x값은 0이고, y값이 양의 값이면 될 것이다.
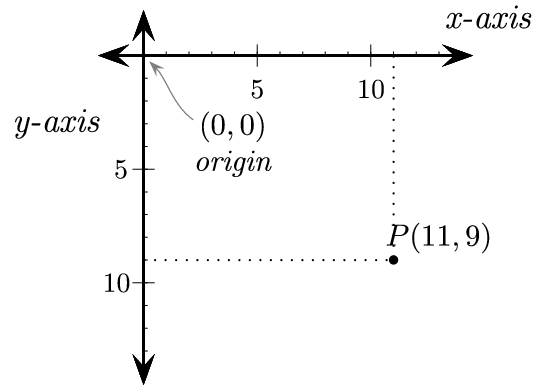
(0, 5)나 (0, 10)이나 둘 다 y축 위에 있으므로 각도가 90°인 벡터가 될 것이다. 다만 그 크기만 다를 뿐이다.
그리고 직관적으로 생각해보면, 어떤 물체의 위치에 계속 (0, 5)를 더해주면 캔버스 좌표계에서 계속 밑으로만 내려갈 것이고, 이는 곧 90°방향으로 움직인다는 것을 쉽게 알 수 있다.
그렇다면, 45°를 나타내는 벡터는 어떻게 표현할까? 마찬가지로 원점을 기준으로 시계방향으로 45°에 위치한 벡터를 하나 정하면 된다.
삼각함수 사용하기
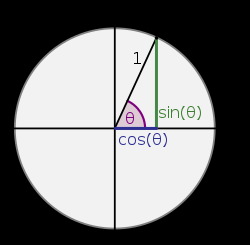
원과 삼각함수에서, (x, y)의 좌표는 각각 x = r⋅cosθ, y = r⋅sinθ로 나타낼 수 있다고 했다.
우린 45°를 나타내고자 한다. 그렇다면 θ는 45°이고, 이는 라디안으로 π/4이다. r이 1인 원에서 45°에 위치한 벡터는 간단히 (x, y) = (cos π/4, sin π/4)가 될 것이다.
const angle = Math.PI/4
const vector = {
x: Math.cos(angle),
y: Math.sin(angle)
}위와 같이 그냥 나타내면 된다.
이 벡터를 이용해서 이전 챕터에서 배웠던 방법대로 원을 움직이게 해보자.
// ----- 이전 챕터에서 계속 사용했던 코드 -----
const canvas = document.querySelector('#canvas')
const ctx = canvas.getContext('2d')
const W = canvas.width = window.innerWidth
const H = canvas.height = window.innerHeight
class Circle {
constructor(x, y, radius) {
this.x = x
this.y = y
this.radius = radius
}
draw() {
ctx.beginPath()
ctx.arc(this.x, this.y, this.radius, 0, Math.PI*2)
ctx.fill()
}
}
// ----- 여기서부터 오늘 배운 내용과 관련된 코드 -----
// 45° 값
const angle = Math.PI/4
// 45°를 나타내는 속도 벡터
const v = {
x: Math.cos(angle),
y: Math.sin(angle),
}
// 원의 위치는 화면의 중앙이다.
const c = new Circle(W/2, H/2, 50)
function render() {
// 원의 위치를 벡터를 이용해 조절한다.
c.x += v.x
c.y += v.y
ctx.clearRect(0, 0, W, H)
c.draw()
requestAnimationFrame(render)
}
render()이를 실행시켜보면, 45°방향으로 움직이는 원을 볼 수 있을 것이다.
다음엔?
속도 벡터를 이용해서 원을 움직이게 해보았다. 이제 우리는 원하는 방향으로 원을 움직이게 할 수 있게 되었다.
다음시간부터는 여러 챕터에 걸쳐서 Glowing Nodes라는 코드펜의 예제를 하나 따라서 만들어 볼 것이다.

