12. 프림 알고리즘

최소 신장 트리

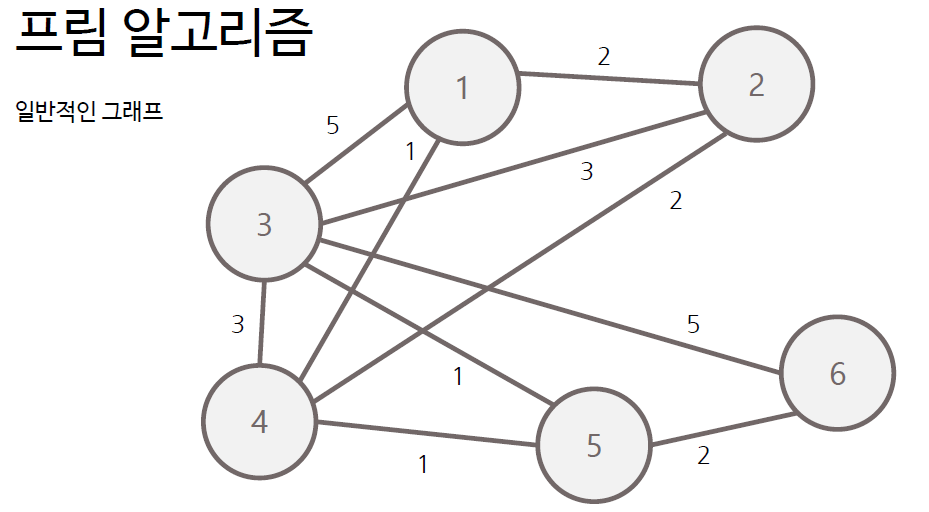
• 신장 트리란 특정한 그래프에서 모든 정점을 포함하는 그래프
• 최소 신장 트리는 스패닝 트리 중에서 간선의 가중치 합이 가장 작은 트리

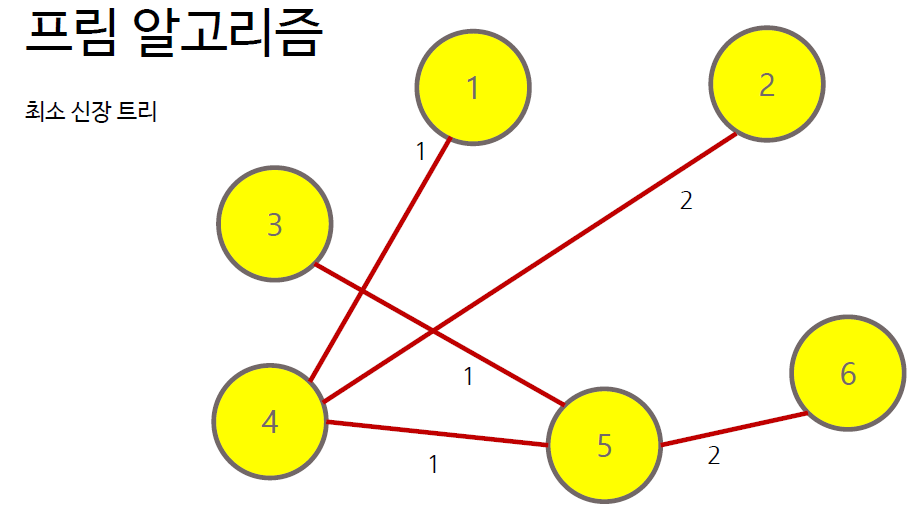
프림 알고리즘의 순서

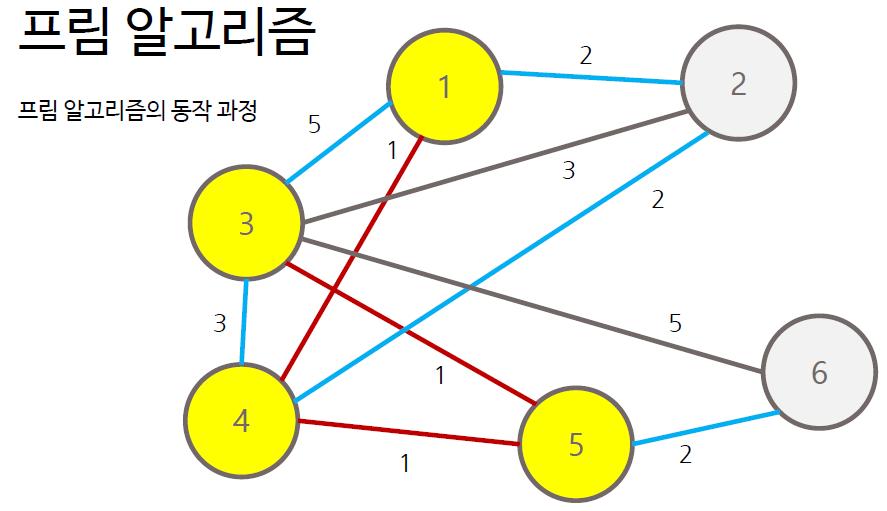
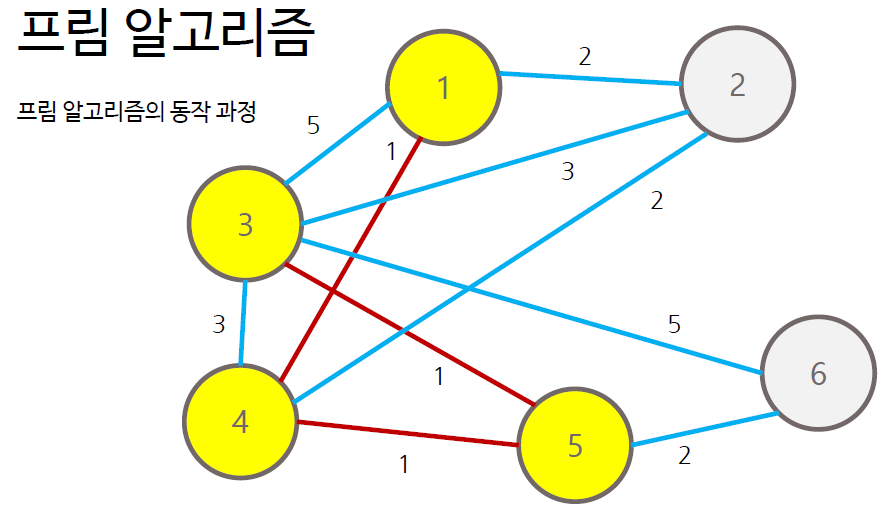
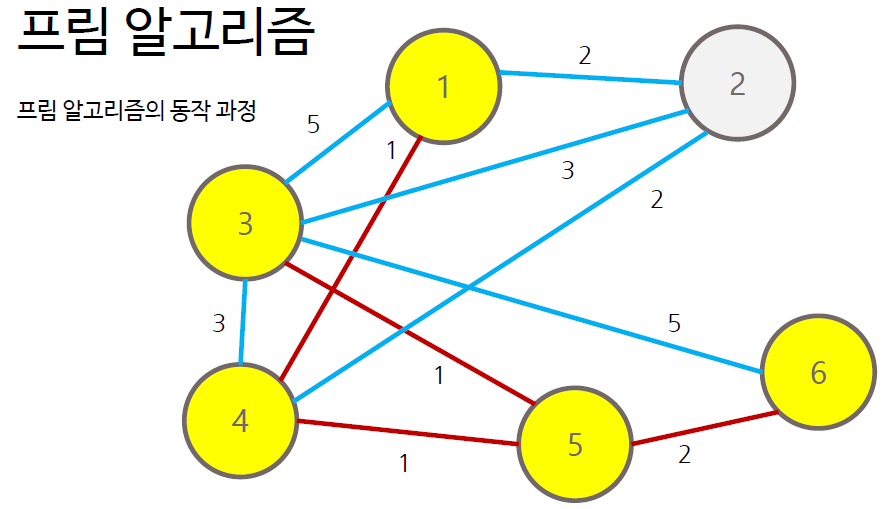
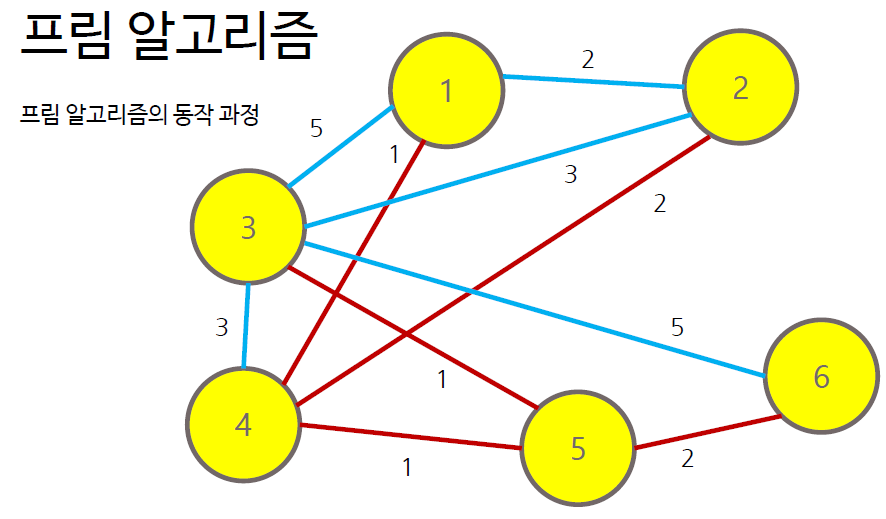
1. 그래프에서 정점 하나를 선택하여 트리 T에 포함
2. T에 포함된 노드와 T에 포함되지 않는 노드 사이의 간선 중 가중치가 가장 작은 간선 찾기
3. 해당 간선에 연결된 T에 포함되지 않은 노드를 트리 T에 포함
4. 모든 노드가 포함될 때까지 과정 반복

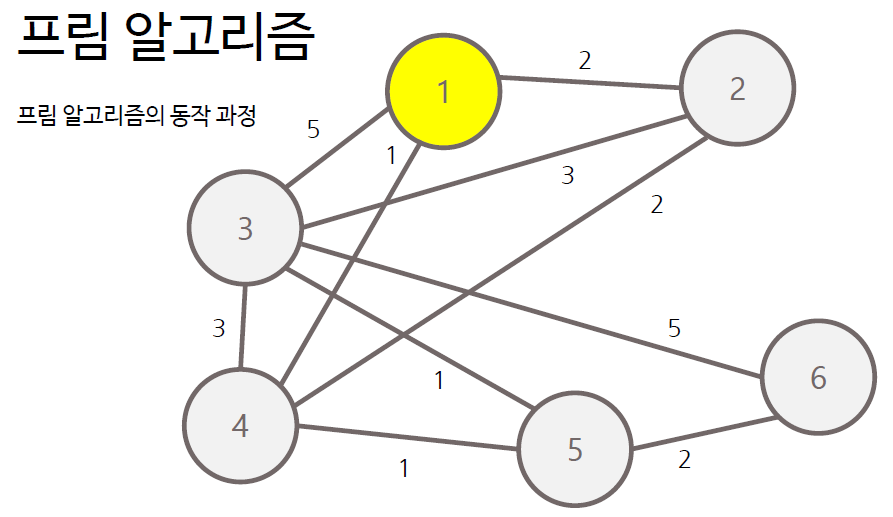
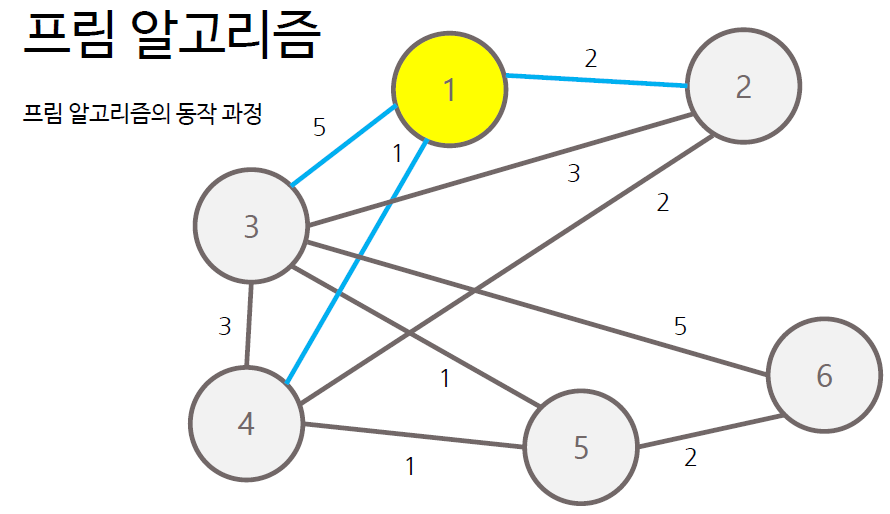
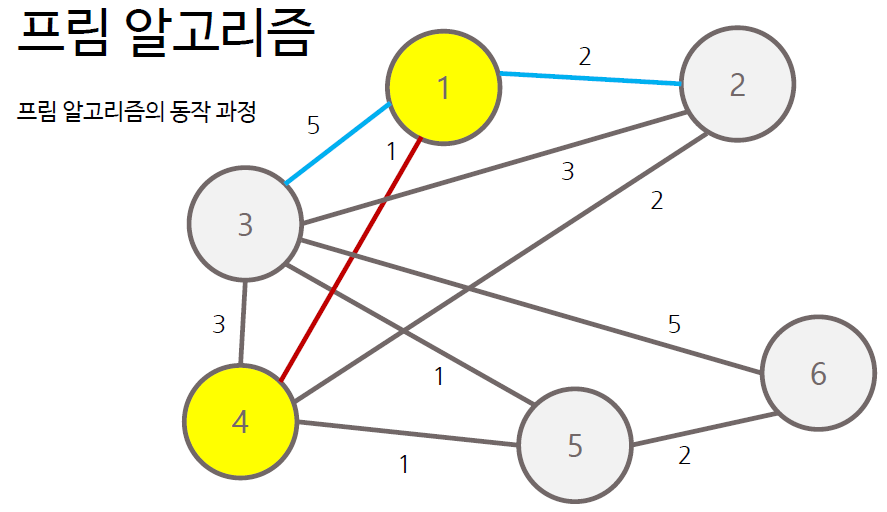
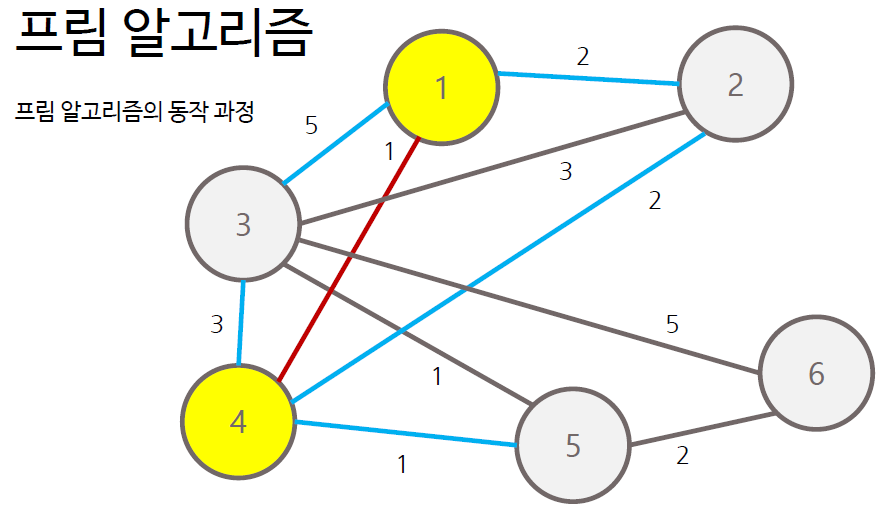
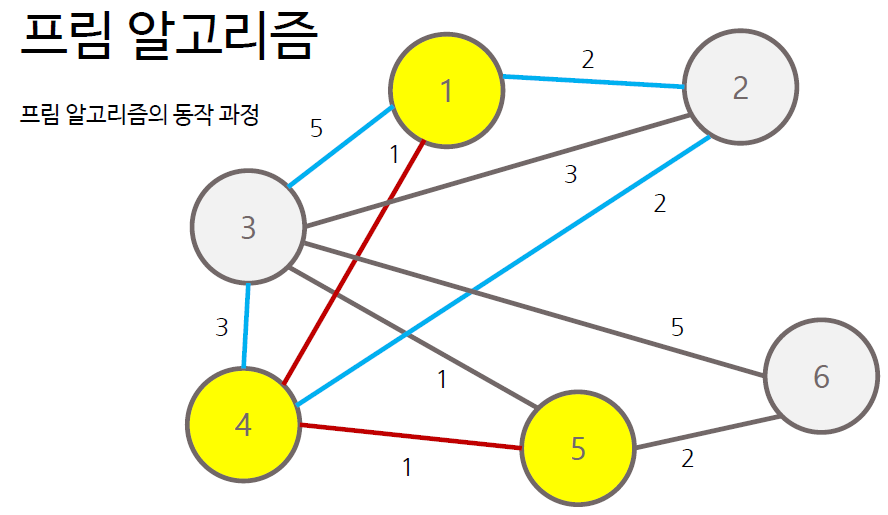
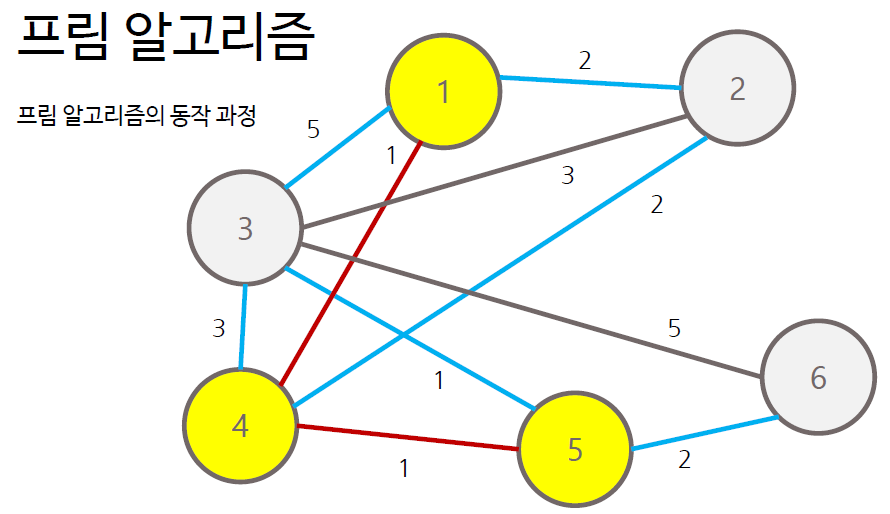
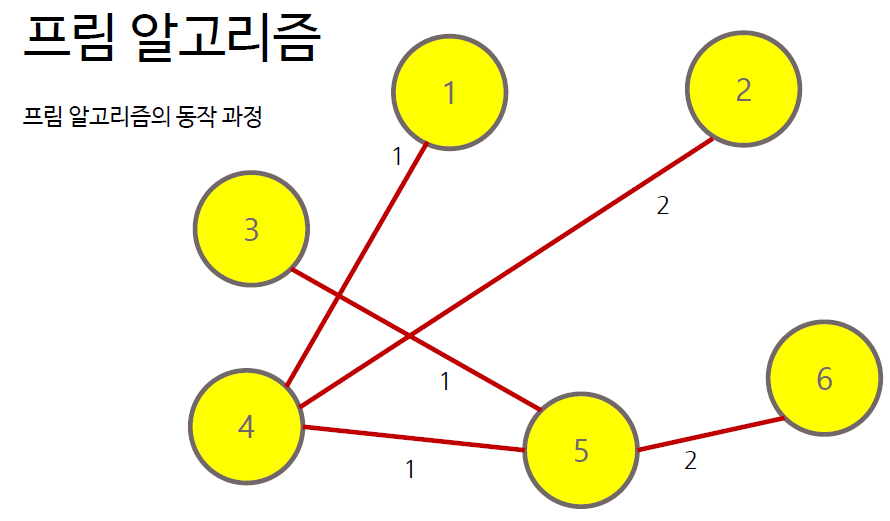
프림 알고리즘은 각 간선에 대한 정보를 우선순위 큐에 담아 처리하는 방식으로 구현

프림 알고리즘의 구현

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <limits.h>
#define NODE_MAX 1001
#define EDGE_MAX 200001 // 양방향 간선이므로 100,000 개 * 2

// 간선구조체 정의
typedef struct {
    int cost;
    int node;
} Edge;

// 교환 함수
void swap(Edge* a, Edge* b) {
    Edge temp;
    temp.cost = a->cost;
    temp.node = a->node;
    a->cost = b->cost;
    a->node = b->node;
    b->cost = temp.cost;
    b->node = temp.node;
}

// 우선 순위 큐
typedef struct {
    int heap[EDGE_MAX];
    int count;
} priorityQueue;

// 삽입 함수
void push(priorityQueue* pq, Edge *edge) {
    if (pq->count >= EDGE_MAX) return;
    pq->heap[pq->count] = edge;
    int now = pq->count;
    int parent = (pq->count - 1) / 2;

    // 새 원소 삽입 후 상향식으로 힙 구성
    while (now > 0 && pq->heap[now]->cost < pq->heap[parent]->cost) {
        swap(pq->heap[now], pq->heap[parent]);
        now = parent;
        parent = (parent - 1) / 2;
    }
    pq->count++;
}

// 추출 함수
int pop(priorityQueue* pq) {
    if (pq->count <= 0)return NULL; // 더 이상 추출할 것이 없을 경우
    Edge* res = pq->heap[0]; // 루트 노드 값을 담아 둠
    pq->count--;
    pq->heap[0] = pq->heap[pq->count]; // 마지막 원소를 루트 노드로 넣음
    int now = 0, leftChild = 1, rightChild = 2;
    int target = now;

    // 새 원소 추출 후 하향식으로 힙 구성
    while (leftChild < pq->count) {
        if (pq->heap[target]->cost > pq->heap[leftChild]->cost)target = leftChild;
        if (pq->heap[target]->cost > pq->heap[rightChild]->cost && rightChild < pq->count) target = rightChild;
        if (target == now) break; // 더 이상 내려가지 않아도 될 때 종료
        else {
            swap(pq->heap[now], pq->heap[target]);
            now = target;
            leftChild = now * 2 + 1;
            rightChild = now * 2 + 2;
        }
    }
    return res;
}

// 간선 연결 리스트 구현
typedef struct Node {
    Edge* data;
    struct Node* next;
} Node;

Node** adj;
int d[NODE_MAX];

void addNode(Node** target, int index, Edge* edge) {
    if (target[index] == NULL) {
        target[index] = (Node*)malloc(sizeof(Node));
        target[index]->data = edge;
        target[index]->next = NULL;
    }
    else {
        Node* node = (Node*)malloc(sizeof(Node));
        node->data = edge;
        node->next = target[index];
        target[index] = node;
    }
}

// main
int main(void) {
    int n, m;
    scanf("%d %d", &n, &m);
    adj = (Node**)malloc(sizeof(Node*) * (n + 1));
    for (int i = 1;i <= n;i++) {
        adj[i] = NULL;
    }

    priorityQueue* pq;
    pq = (priorityQueue*)malloc(sizeof(priorityQueue));
    pq->count = 0;

    for (int i = 0;i < m;i++) {
        int a, b, c;
        scanf("%d %d %d", &a, &b, &c);
        Edge* edge1 = (Edge*)malloc(sizeof(Edge));
        edge1->node = b;
        edge1->cost = c;
        addNode(adj, a, edge1);

        Edge* edge2 = (Edge*)malloc(sizeof(Edge));
        edge2->node = a;
        edge2->cost = c;
        addNode(adj, b, edge2);
    }

    // 프림 알고리즘 시작
    long long res = 0;
    Edge* start = (Edge*)malloc(sizeof(Edge));
    start->cost = 0;
    start->node = 1;
    push(pq, start);

    for (int i = 1;i <= n;i++) {
        int nextNode = -1, nextCost = INT_MAX;
        while (1) {
            Edge* now = pop(pq);
            if (now == NULL) break;
            nextNode = now->node;

            if (!d[nextNode]) {
                nextCost = now->cost;
                break;
            }
        }

        if (nextCost == INT_MAX) printf("연결 그래프가 아닙니다.\n");
        res += nextCost;
        d[nextCost] = 1;
        Node* cur = adj[nextCost];

        while (cur != NULL) {
            push(pq, cur->data);
            cur = cur->next;
        }
    }
    printf("%lld\n", res);
    system("pause");
    return 0;
}

프림 알고리즘은 최소 스패닝 트리를 구하는 과정에서 O(E log V)의 시간 복잡도를 가짐

E : 모든 간선의 정보를 큐에 넣어서 처리하는 데 필요한 시간 복잡도
log V : 큐에서 원소를 꺼낼 때 필요한 시간 복잡도