11.AVL 트리

AVL 트리의 정의

• 균형이 갖춰진 이진트리
• 완전 이진 트리는 검색 시 O(log N)의 시간 복잡도 유지
• AVL 트리는 간단한 구현으로 완전 이진 트리에 가까운 형태가 되도록 함

AVL은 해당 논문을 발표한 G.M. Adelson-Velskii와 E.M. Landis의 이름을 따서 지은 이름

AVL 트리는 균형 인수(Balance Factor) 개념 사용

균형 인수 = | 왼쪽 자식 높이 - 오른쪽 자식 높이|

--> 균형 인수가 2 이상 차이가 날 때 문제가 있다고 판단

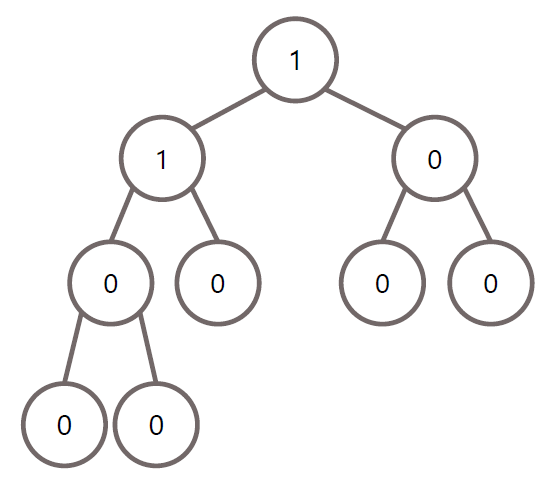
따라서 모든 노드에 대한 균형 인수가 +1, 0, -1인 트리를 의미
그렇지 않은 경우 '회전(Rotation)'을 통해 트리를 재구성

AVL 트리의 회전

AVL 트리는 총 4가지 형식에 의해 균형이 깨질 수 있음
균형이 깨지는 노드를 X라고 가정

형식	설명
LL	X의 왼쪽 자식의 왼쪽에 삽입하는 경우
LR	X의 왼쪽 자식의 오른쪽에 삽입하는 경우
RR	X의 오른쪽 자식의 오른쪽에 삽입하는 경우
RL	X의 오른쪽 자식의 왼쪽에 삽입하는 경우

초기 상태

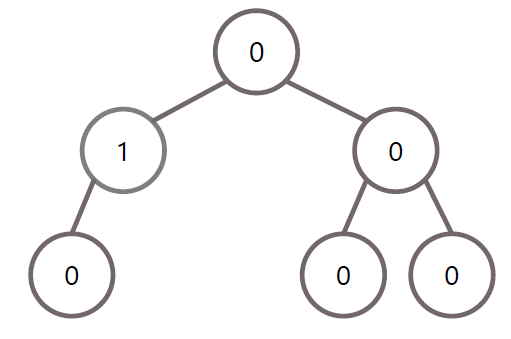
LL 회전 조건

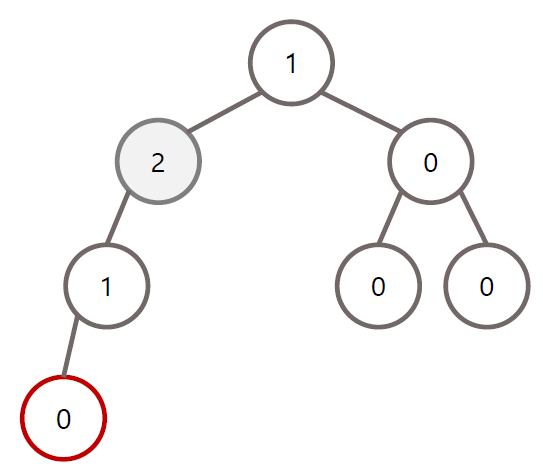
LR 회전 조건

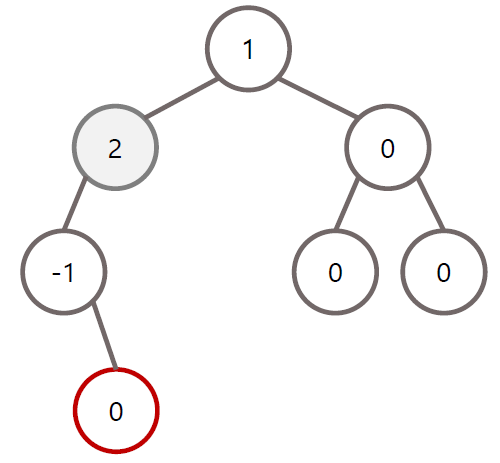
초기 상태

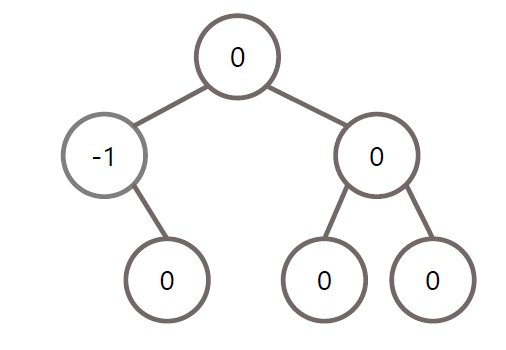
RR 회전 조건

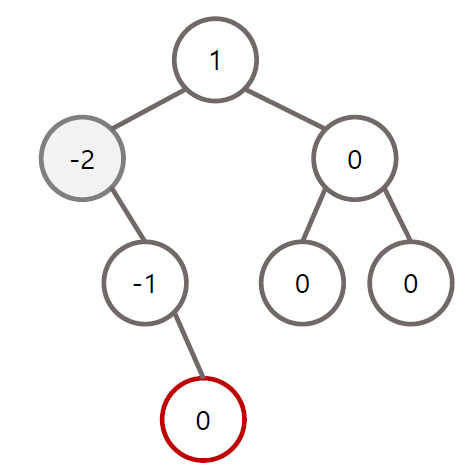
RL 회전 조건

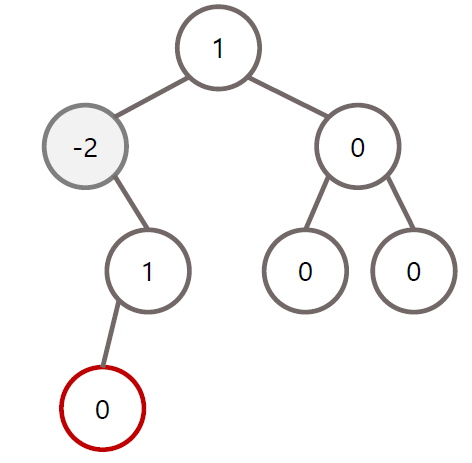
AVL 트리의 높이

AVL 트리의 각 노드는 '균형 인수'를 계산하기 위해 자신의 '높이'값을 가짐

AVL 트리의 LL 회전

노드 X를 기준으로 LL 회전을 수행

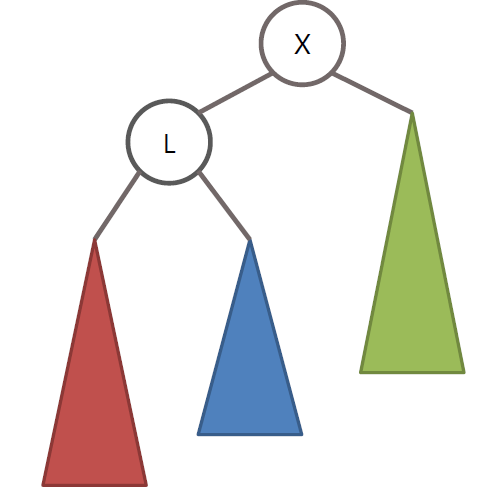
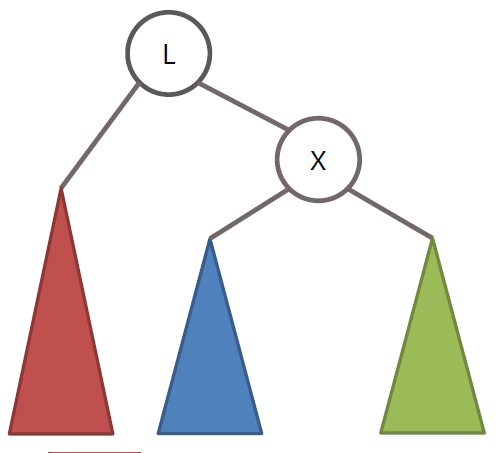
RR 회전은 LL 회전의 정반대

AVL 트리의 LR 회전

왼쪽 노드인 L 노드를 기준으로 RR 회전을 수행 후 노드 X를 기준으로 LL 회전 수행

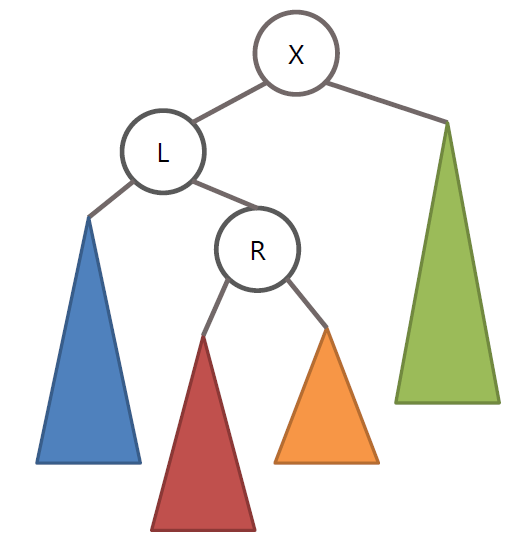
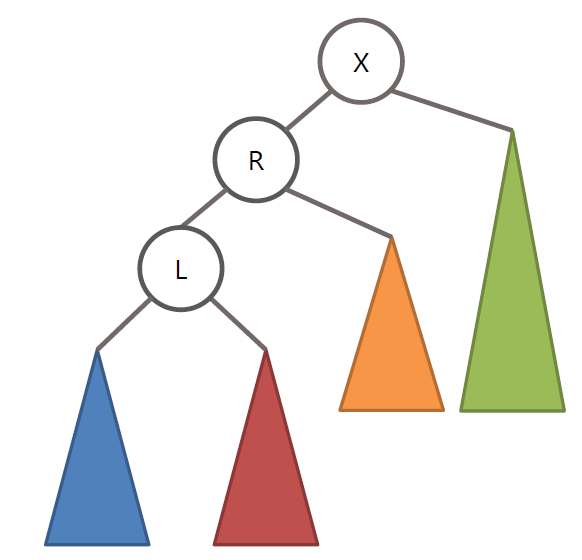
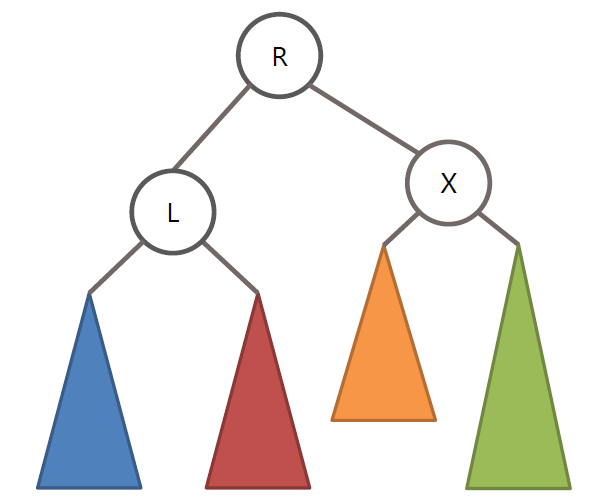
RL 회전 또한 LR 회전의 정 반대

AVL 트리의 균형 잡기

• AVL 트리의 균형 잡기는 각 노드가 삽입 될 때마다 수행
• 삽입 과정에 시간 복잡도는 O(log N)
• 각 트리의 균형 잡기는 삽입 시 모든 노드에 대해 수행되기에 O(1)의 시간 복잡도를 만족해야 함

AVL 트리의 삽입과 출력

삽입 : 일반적인 이진 탐색 트리와 흡사하지만 삽입 시 모든 노드에 대해 균형 잡기를 수행

출력 : 트리의 너비가 높이보다 크기때문에 세로 방향으로 출력

AVL 트리의 구현

#include <stdio.h>
#include <stdlib.h>

// 최대값찾기 함수
int getMax(int a, int b) {
	if (a > b) return a;
	return b;
}

// 노드 구현
typedef struct {
	int data;
	int height; // 높이를 저장해야 시간 복잡도를 보장할 수 있음
	struct Node* leftChild;
	struct Node* rightChild;
} Node;

// 높이 구하는 함수
int getHeight(Node* node) {
	if (node == NULL) return 0;
	return node->height;
}

// 모든 노드는 회전을 수행한 이후에 높이 재계산
void setHeight(Node* node) {
	node->height = getMax(getHeight(node->leftChild), getHeight(node->rightChild)) + 1;
}

// 균형 인수 계산 함수
int getDifference(Node* node) {
	if (node == NULL) return 0;
	Node* leftChild = node->leftChild;
	Node* rightChild = node->rightChild;
	return getHeight(leftChild) - getHeight(rightChild);
}

// LL 회전
Node* rotateLL(Node* node) {
	Node* leftChild = node->leftChild;
	node->leftChild = leftChild->rightChild;
	leftChild->rightChild = node;
	setHeight(node); // 회전 이후 높이 다시 계산
	return leftChild;
}

// RR 회전
Node* rotateRR(Node* node) {
	Node* rightChild = node->rightChild;
	node->rightChild = rightChild->leftChild;
	rightChild->leftChild = node;
	setHeight(node); // 회전 이후 높이 다시 계산
	return rightChild;
}

// LR 회전
Node* rotateLR(Node* node) {
	Node* leftChild = node->leftChild;
	node->leftChild = rotateRR(leftChild);
	return rotateLL(node);
}

// RL 회전
Node* rotateRL(Node* node) {
	Node* rightChild = node->rightChild;
	node->rightChild = rotateLL(rightChild);
	return rotateRR(node);
}

// 균형 잡기
Node* balance(Node* node) {
	int difference = getDifference(node);
	if (difference >= 2) {
		// LL, LR  형식 판별 후 균형 잡기
		if (getDifference(node->leftChild) >= 1) {
			node = rotateLL(node);
		}
		else {
			node = rotateLR(node);
		}
	}
	else if (difference <= -2) {
		// RR, RL 형식 판별 후 균형 잡기
		if (getDifference(node->rightChild) <= -1) {
			node = rotateRR(node);
		}
		else {
			node = rotateRL(node);
		}
	}
	setHeight(node); // 회전 이후 높이 재계산
	return node;
}

// 삽입 함수
Node* insertNode(Node* node, int data) {
	if (!node) {
		node = (Node*)malloc(sizeof(Node));
		node->data = data;
		node->height = 1;
		node->leftChild = node->rightChild = NULL;
	}
	// 삽입 후 항상 균형 잡기 실행
	else if (data < node->data) {
		node->leftChild = insertNode(node->leftChild, data);
		node = balance(node);
	}
	else if (data > node->data) {
		node->rightChild = insertNode(node->rightChild, data);
		node = balance(node);
	}
	else {
		printf("데이터 중복 발생");
	}
	return node;
}

// 출력 함수
Node* root = NULL;

void display(Node* node, int level) {
	if (node != NULL) {
		// 가장 우측 노드부터 방문
		display(node->rightChild, level + 1);
		printf("\n");

		if (node == root) {
			printf("ROOT : ");
		}

		for (int i = 0;i < level && node != root;i++) {
			printf("     ");
		}
		printf("%d(%d)", node->data, getHeight(node));
		display(node->leftChild, level + 1);
	}
}

int main(void) {
	root = insertNode(root, 7);
	root = insertNode(root, 6);
	root = insertNode(root, 5);
	root = insertNode(root, 3);
	root = insertNode(root, 1);
	root = insertNode(root, 9);
	root = insertNode(root, 8);
	root = insertNode(root, 12);
	root = insertNode(root, 16);
	root = insertNode(root, 18);
	root = insertNode(root, 23);
	root = insertNode(root, 21);
	root = insertNode(root, 14);
	root = insertNode(root, 15);
	root = insertNode(root, 19);
	root = insertNode(root, 20);
	display(root, 1);
	printf("\n");
	system("pause");
	return 0;
}

AVL 트리를 이용해 탐색하면 O(log N)의 시간 복잡도 유지 가능