07. 부울대수와 논리식

Boolean Algebra

참, 거짓을 판별할 수 있는 논리적 명제를 수학적으로 표현한 논리이다. 전개식으로 구현한 것은 1854년 영국의 수학자 부울이다.

부울 대수의 기본 법칙

교환법칙

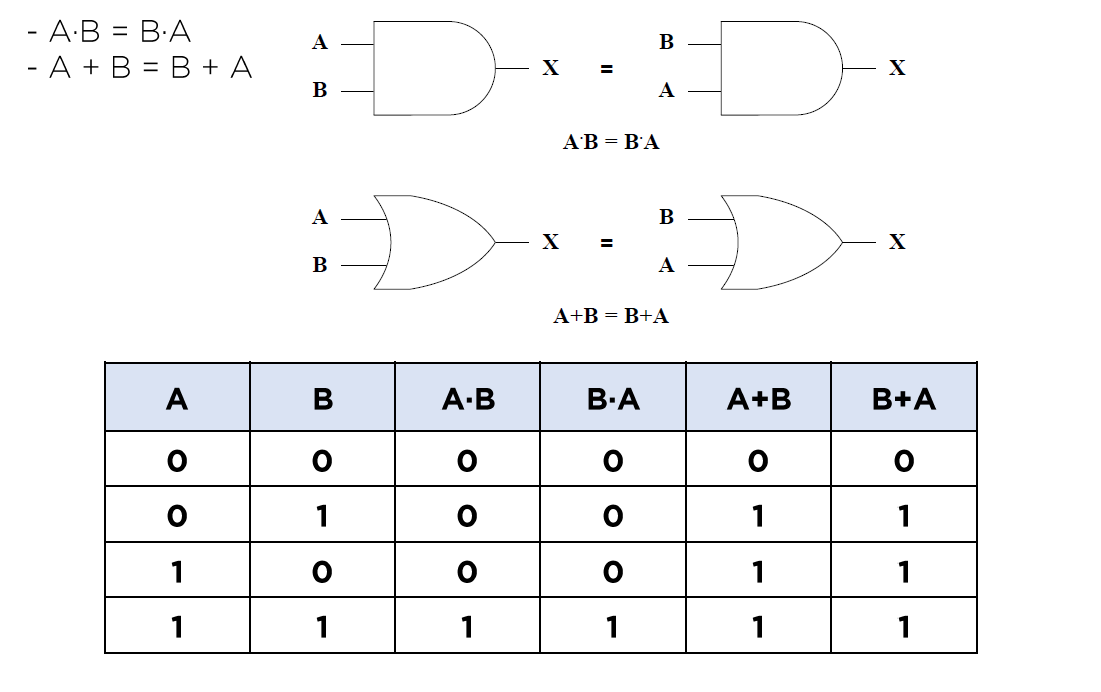
결합법칙

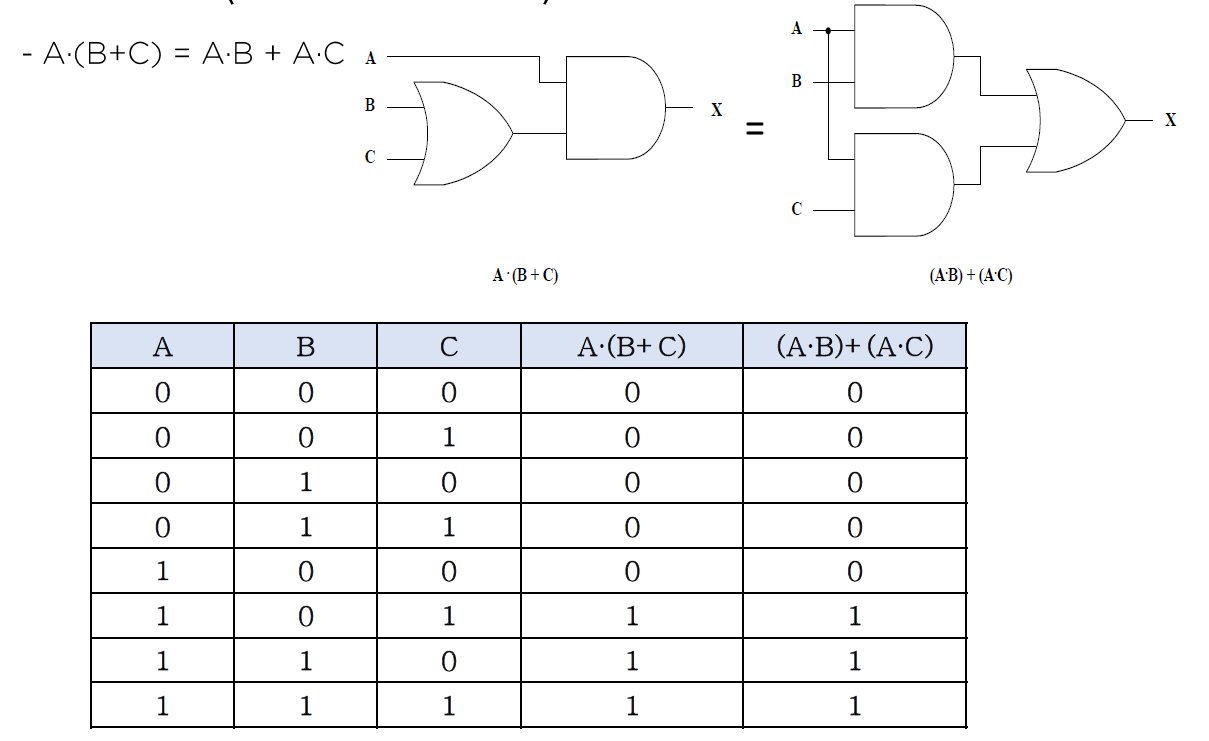
분배법칙

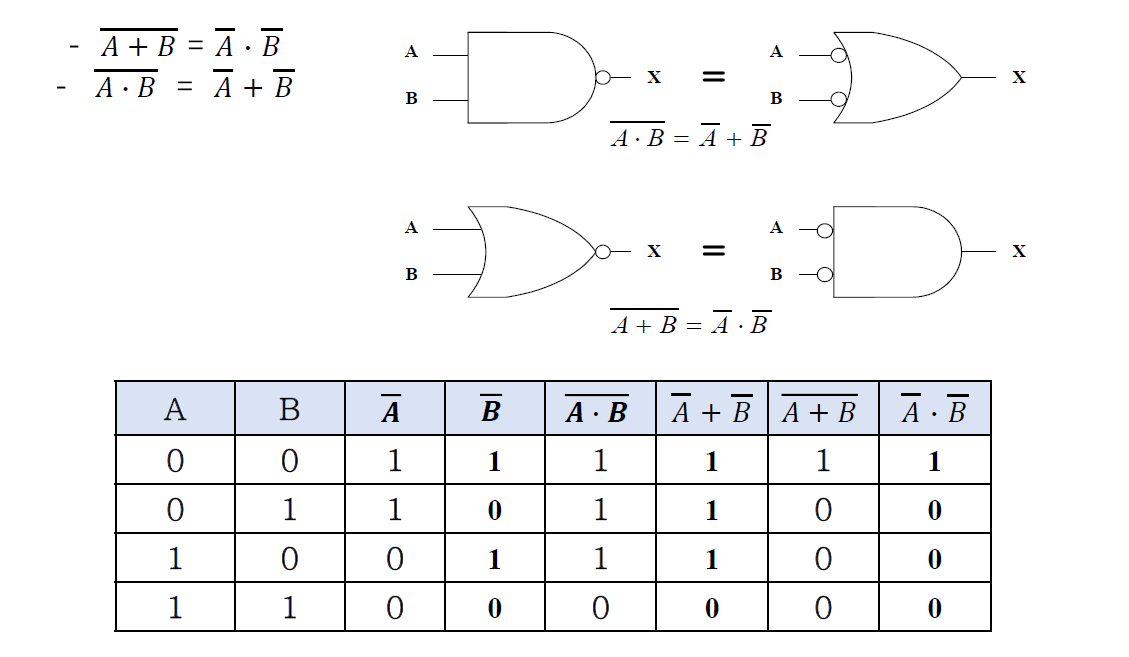
드모르간의 법칙

논리식의 간편화

위의 규칙들을 활용하여 논리식을 간편화 할 수 있으며 다른 방법으로는 카노맵을 활용하여 간편화 할 수 있다.

기본방법

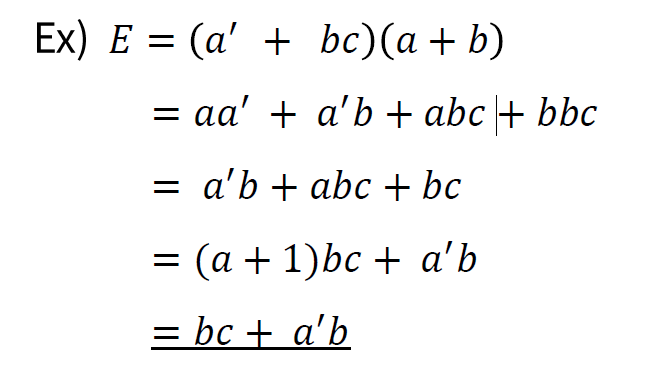
Karnaugh Map

이 카노맵을 사용하면 부울 함수를 곧바로 간소화할 수 있고 시각적으로 보기 편하기에 널리 활용된다.

카노맵 표현 방법

• 만약 변수가 n개라면 카노맵은 2^n개의 minterm으로 구성된다
• 각 인접 민텀은 하나의 변수만이 변경되어야 한다
• 출력이 1인 기본곱에 해당하는 minterm은 1로, 나머지는 0으로 표시

카노맵을 활용한 예