문제
https://www.acmicpc.net/problem/2579
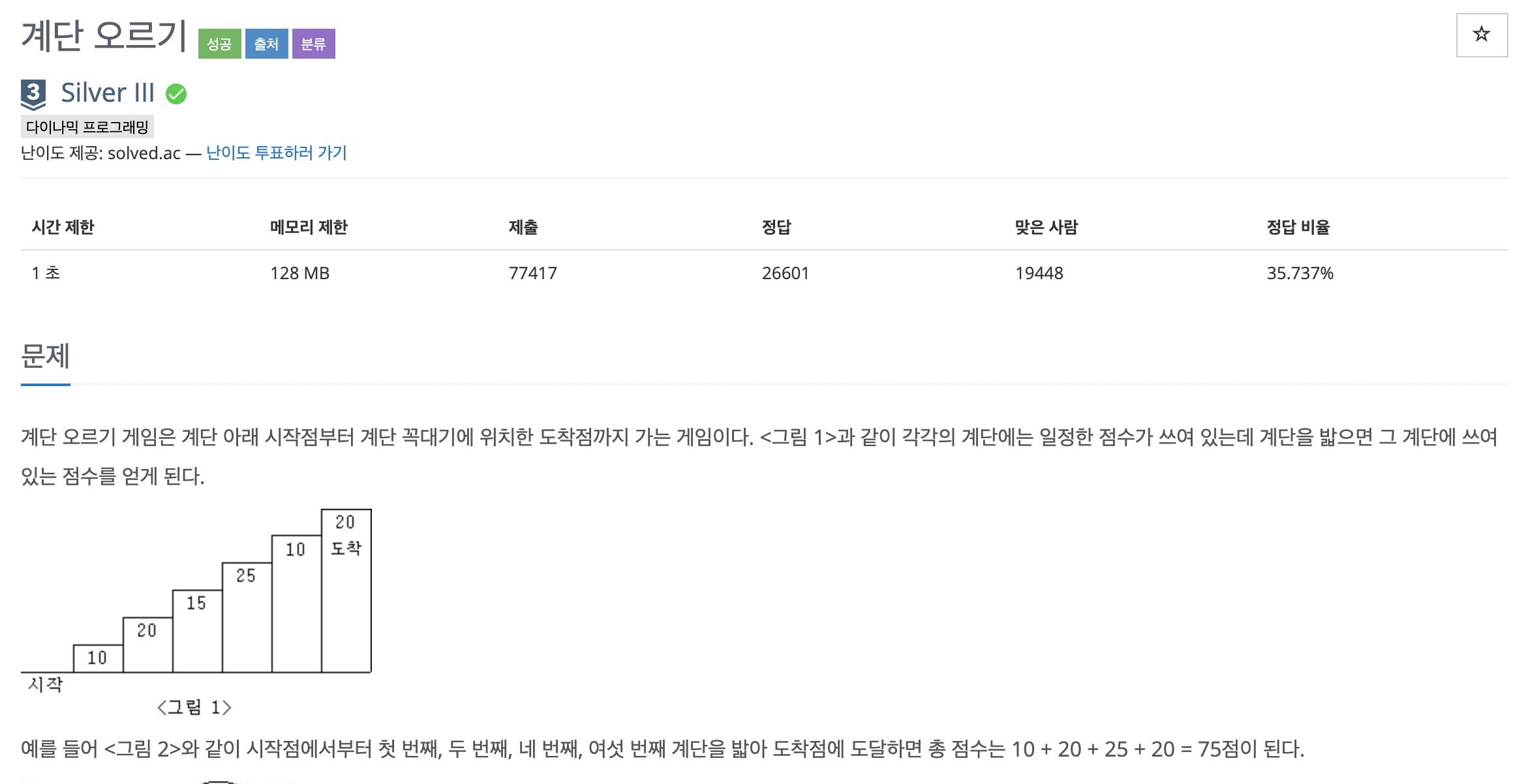
세가지 규칙을 만족시키면서 얻을 수 있는 최댓값을 구하는 문제다.
조건
1. 계단은 한칸 혹은 두칸만 오를 수 있다.
2. 연속으로 세칸을 오를 수 없다.
3. 가장 마지막 칸을 반드시 밟아야한다.
문제 풀이
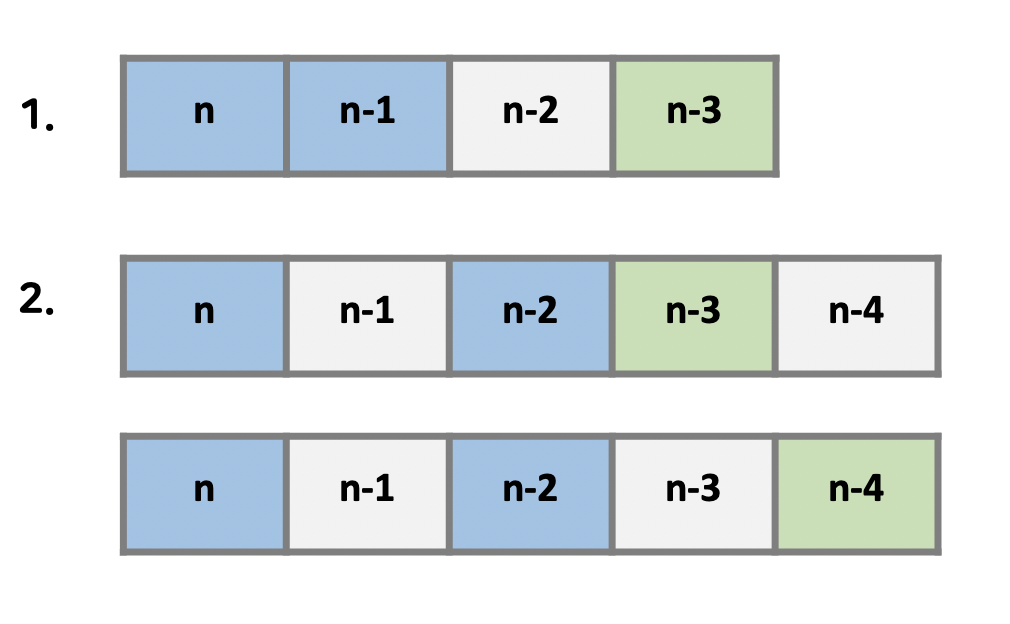
마지막 칸을 n번째 칸이라고 했을 때, 반드시 밟아야 하기 때문에 경우는 두가지로 생각할 수 있다.
- n번째 ➣ n-1번째칸
- n번째 ➣ n-2번째칸
1번의 경우에는 연속으로 3칸을 밟을 수 없기 때문에 반드시 n-3번째 칸을 밟아야한다. 그래서 조건을 추가해서 다음과 같이 수정할 수 있다.
- n번째 ➣ n-1번째 ➣ n-3번째칸
2번의 경우에는 n-3, n-4 둘다 가능하기 때문에 그 이후엔 고려할 필요 없다.
따라서 우리가 고려해야 할 상황은 두가지로 정리할 수 있다.
이 두가지 중 더 큰 값을 골라서 dp 배열에 넣어주기만 하면 된다.
- n번째 ➣ n-1번째칸 ➣ n-3번째칸
- n번째 ➣ n-2번째칸
dp 배열에는 각 칸에서 가질 수 있는 최대값을 담는다.
위에서 정의한 두가지 경우를 고려해주기 위해 점화식을 정리해보자.
- (n-3)번째 칸과 (n-1)번째칸을 밟고, n번째 칸을 밟는 경우
➣ (n-3)번째 칸까지의 최댓값 + (n-1)번째 칸 + n번째 칸
➣dp[n-3]+stairs[n-1]+stairs[n]
- (n-2)번째 칸을 밟고, n번째 칸을 밟는 경우
➣ (n-2)번째 칸까지의 최댓값 + n번째 칸
➣dp[n-2]+stairs[n]
bottom-up 방식을 사용하기 위해 dp[0],dp[1], dp[2]는 직접 할당해주었다.
- dp[0] : 0번째 칸이 가질 수있는 최대값은 0번째 칸인
stairs[0]이다. - dp[1] : 1번째 칸이 가질 수있는 최대값은 0번째 칸과 1번째 칸의 값의 합인
stairs[0] + stairs[1]이다. - dp[2] : 2번째 칸이 가질 수있는 최대값은
stairs[0]+stairs[2]와stairs[1]+stairs[2]중 큰 값을 담아준다.
코드
import sys
input = sys.stdin.readline
n = int(input().rstrip())
stairs=[]
dp = [0] * (n+1)
for _ in range(n):
temp = int(input().rstrip())
stairs.append(temp)
dp[0]=stairs[0]
if n==1:
print(dp[0])
sys.exit(0)
dp[1]=stairs[1]+stairs[0]
if n==2:
print(dp[1])
sys.exit(0)
dp[2]=max(stairs[0]+stairs[2],stairs[1]+stairs[2])
for i in range(3,n):
dp[i] = max(dp[i-2]+stairs[i], dp[i-3]+stairs[i-1]+stairs[i])
print(dp[n-1])