문제
https://www.acmicpc.net/problem/9465
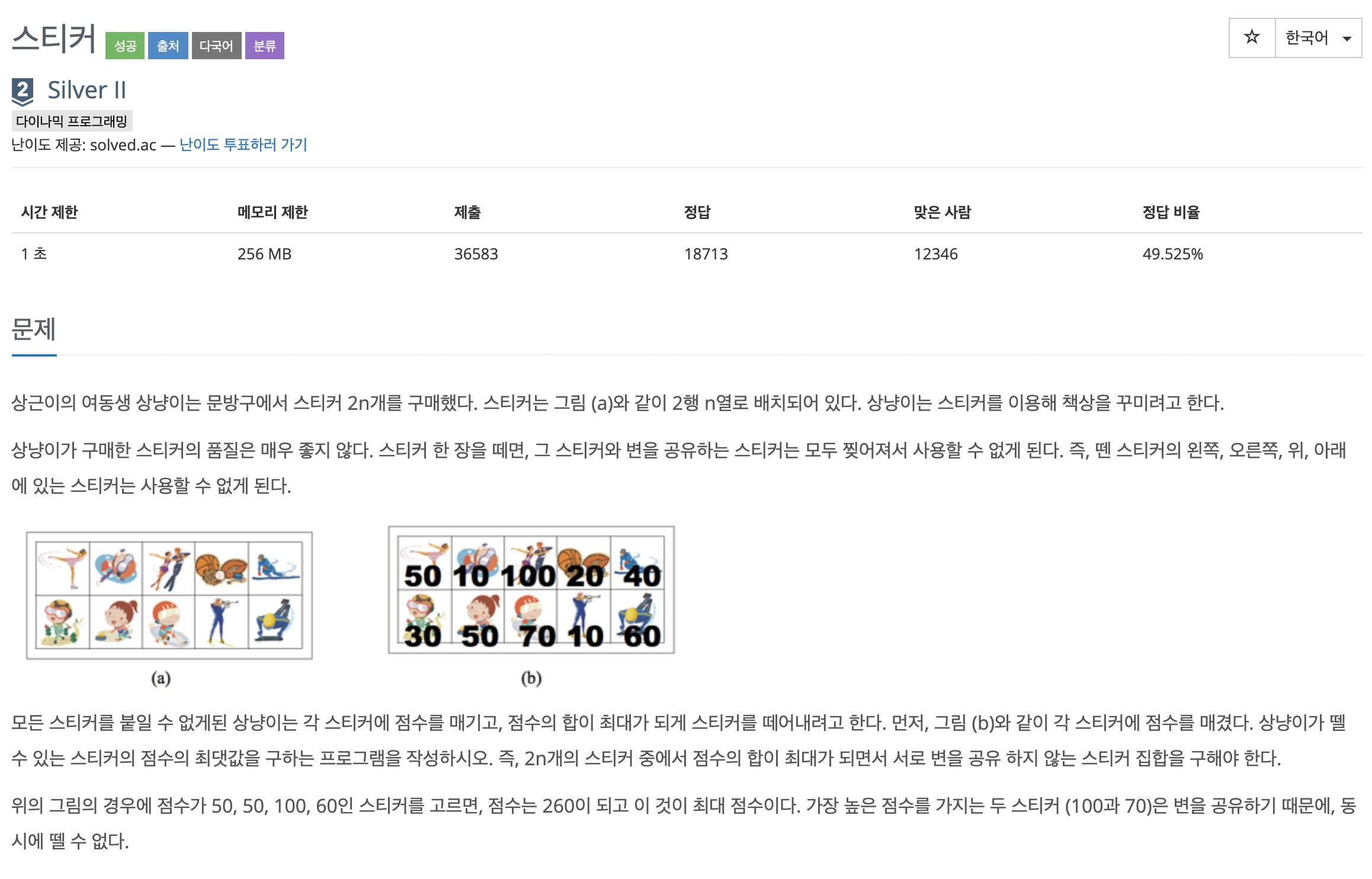
(i,j)에 위치한 스티커를 떼면, 상하좌우가 찢어진다. 🧩
스티커에 뗀 뒤 가장 큰 점수를 구하는 문제다.
문제 풀이
dp[0][i] : 0행 i열까지의 최대값
dp[1][i] : 1행 i열까지의 최대값dp 배열을 확실하게 잡고 가면, 문제 풀기가 수월하다.
우선 2열까지는 값을 지정해주었다.
- 0열 🧩
dp[0][0] = stickers[0][0]
dp[1][0] = stickers[1][0]- 1열 🧩
# 대각선의 최대값 + 현재 위치
# 현재 위치의 스티커를 떼어주면 상하좌우가 찢어지기 때문에
# 대각선의 최댓값을 더해주는 것!
dp[0][1] = dp[1][0] + stickers[0][1]
dp[1][1] = dp[0][0] + stickers[1][1]- n열 🧩
dp[0][n] = 현재 위치의 스티커 값(stickers[0][i])
+ max(
현재 스티커의 대각선 위치까지의 최대값,
0행 (n-2)열까지의 최댓값,
1행 (n-2)열까지의 최댓값
)이 때 (n-2)열을 고려해주는 이유는 (n-1) 열에서 선택하지 않을 때 최댓값을 가질 수도 있기 때문이다.
ex )
input>
100 1 1 100
1 1 100 1
output>
300
# 2열을 선택하지 않을 때 최대값을 얻을 수 있다.코드
import sys
input = sys.stdin.readline
T = int(input())
for _ in range(T):
# 2행 n열
n = int(input())
stickers = []
for _ in range(2):
stickers.append(list(map(int, input().rsplit())))
# dp[0][i] : 0행 i열까지의 최대값, dp[1][i] : 1행 i열까지의 최대값
dp = [[0 for _ in range(n)] for _ in range(2)]
if n == 1:
print(max(stickers[0][0], stickers[1][0]))
elif n == 2:
print(max(stickers[0][0] + stickers[1][1],
stickers[1][0] + stickers[0][1]))
else:
dp[0][0], dp[1][0] = stickers[0][0], stickers[1][0]
dp[0][1], dp[1][1] = stickers[0][1] + stickers[1][0], stickers[0][0] + stickers[1][1]
for i in range(2, n):
dp[0][i] = max(dp[1][i-1], dp[0][i-2], dp[1][i-2]) + stickers[0][i]
dp[1][i] = max(dp[0][i-1], dp[1][i-2], dp[0][i-2]) + stickers[1][i]
print(max(dp[0][n-1], dp[1][n-1]))
