최단 경로 🗺
- 가중치 그래프에서 두 정점 사이의 경로들 중 간선의 가중치 합이 최소인 경로
- 간선 개수와 상관 없이 가중치의 합이 가장 적은 경로를 찾으면 됨!
- 하나의 시작 정점에서 다른 모든 정점까지의 최단 경로
- 다익스트라 알고리즘 : 음의 가중치 허용 X
- 벨만-포드 알고리즘 : 음의 가중치 허용
- 모든 정점에 대한 최단 경로
- 플로이드-워샬 알고리즘
1️⃣ 다익스트라 알고리즘
- 시작 정점에서의 거리가 최소인 정점을 선택해 나가면서 최단 경로를 구하는 방식
- 매번 해당 정점에서 거리가 최소인 정점을 선택하기 때문에 그리디 알고리즘
- Prim 알고리즘과 유사!
BFS와 다익스트라의 차이? 🤔
- BFS : 가중치 없는 그래프에서 출발지-도착지 최단거리
- 다익스트라 : 가중치 있는 그래프에서 출발지-도착지 최단거리
-
로직
-
두 정점 간 경로가 존재하지 않으면 경로의 길이는 INF로 정의
-
아직 방문하지 않은 정점도 INF로 처리

-
특정 노드를 시작 노드로 하고, 연결된 모든 노드 방문
- 해당 정점으로 이동할 때 더 작은 가중치로 값을 바꿔줌
- 시작 노드를 A로 지정
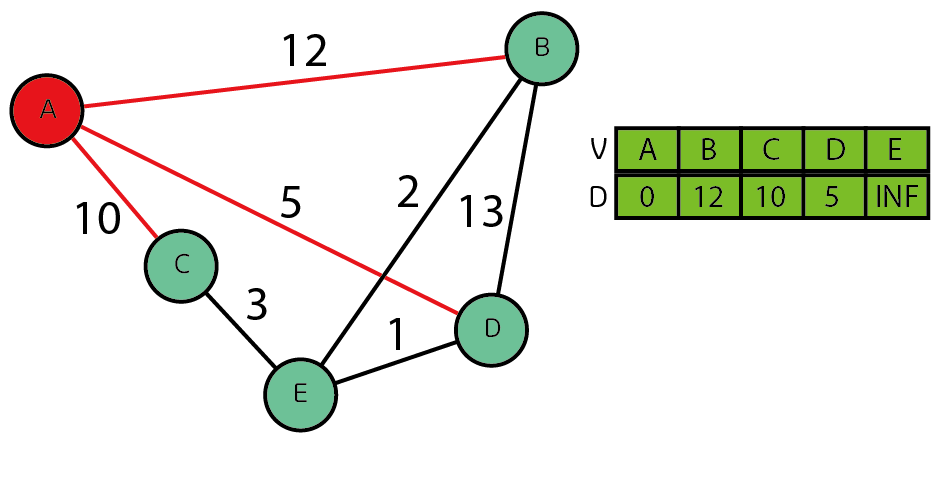
-
방문하지 않은 노드 중 가장 가중치가 낮은 노드를 다음 노드로 선택
- 가장 가중치가 낮은 노드인 D를 다음 노드로 지정

- 다음 노드 또한 연결된 모든 노드를 방문하고, 더 작은 가중치로 값을 바꿔줌
- A ▶ E : INF
- A ▶ D ▶ E = 6
-
모든 노드를 방문할 때까지 방문
-
2️⃣ 플로이드-워샬 알고리즘
-
"모든 정점의 최단 경로를 알려면 어떻게 해야할까?"
-
각 점을 시작점으로 정해서, 다익스트라의 최단 경로 알고리즘을 수행하면 됨
-
시간 복잡도는
O(n^3)이지만, 매우 간단해서 다익스트라보다 효율적 -
정점이 500개일 때, 플로이드-워샬을 사용하면 125,000,000번의 연산만으로 모든 정점의 최단 경로를 알 수 있음
- 약 1.25초
D[i][j] k= 정점 { 1, 2, ... , k} 만을 경유 가능한 정점으로 고려한 뒤, 정점 i부터 j까지 가장 짧은 경로의 길이D[i][j] 0= 정점 i에서 j로 이동할 때, 다른 정점을 경유하지 않고 직접 이동D[i][j] 1= 정점 i -> (1번 정점) -> 정점 j
- 1번 정점을 거쳐오는 것이 더 짧은지,
바로 오는 것이 더 짧은지 비교한 뒤 더 작은 값 대입- min (
D[i][j] 0,D[i][1] 0 + D[1][j] 0);
즉,
D[i][j] k= min (D[i][k] (k-1) + D[k][j] (k-1),D[i][j] (k-1))
D[i][j] = 정점 i에서 j로의 최소 비용
AllPairsShortest(D[][])
for k in 1 -> n :
for i in 1 -> n : // 출발지
for j in 1 -> n: // 도착지
D[i][j] = min(D[i][k] + D[k][j], D[i][j])
