최소 신장 트리

최소 신장 트리?

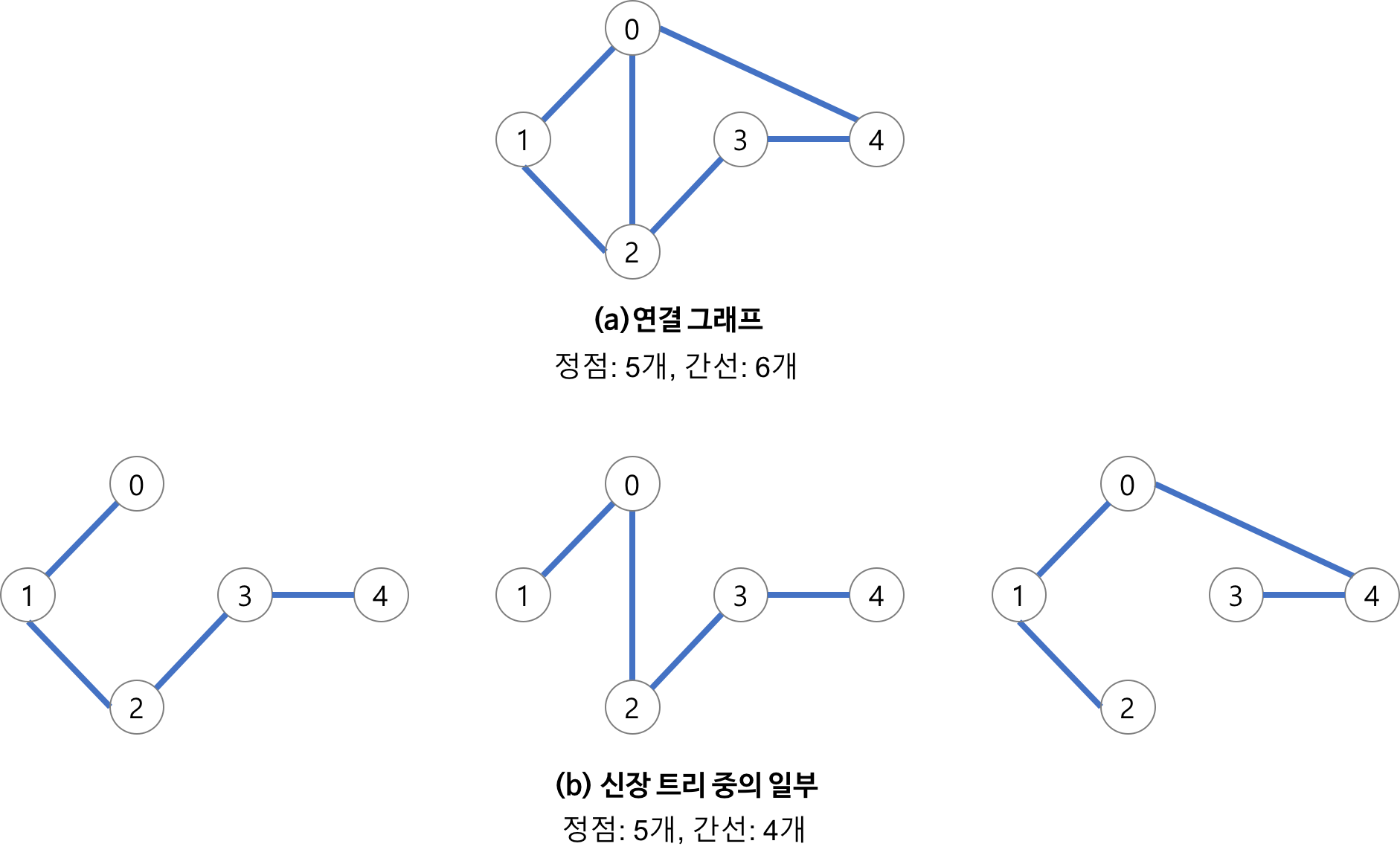
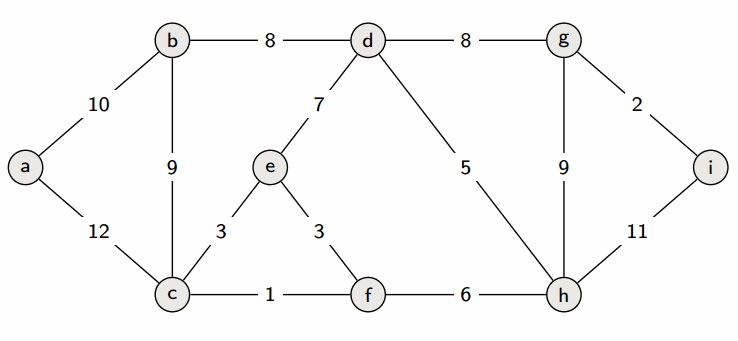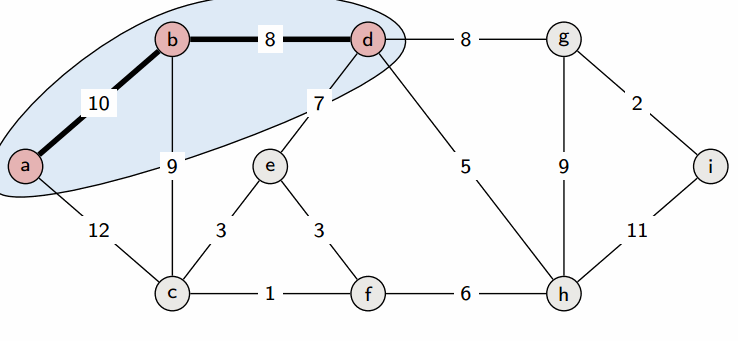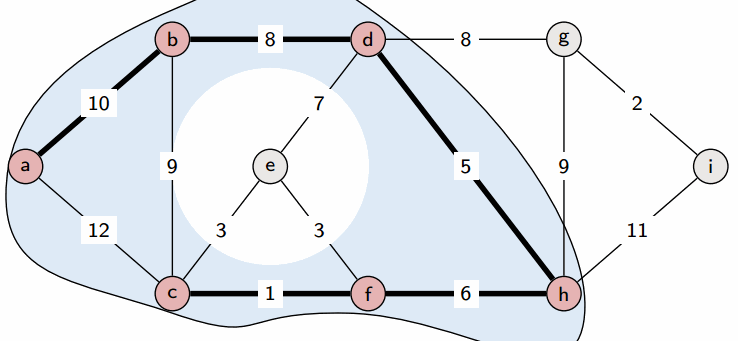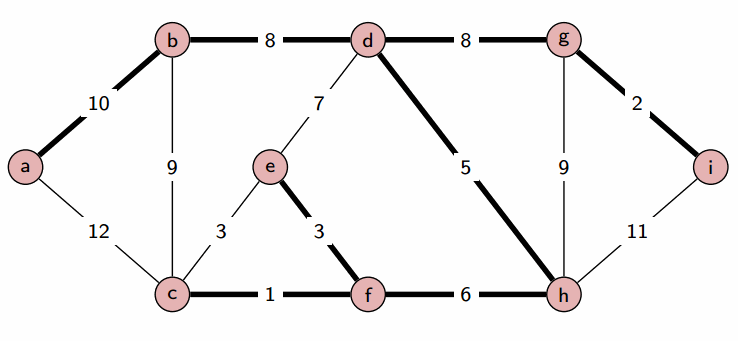
• Minimum Spanning Tree, 최소 스패닝 트리라고도 불림
• 신장 트리를 구성하는 간선들의 가중치의 합이 최소인 신장 트리
• 신장 트리?
  • N개의 정점과 N-1개의 간선으로 이루어진 그래프
  • 어느 정점도 고립되어 있지 않고, 이어져 있음
  • 트리이므로 사이클이 생겨선 안됨!

구현 방법

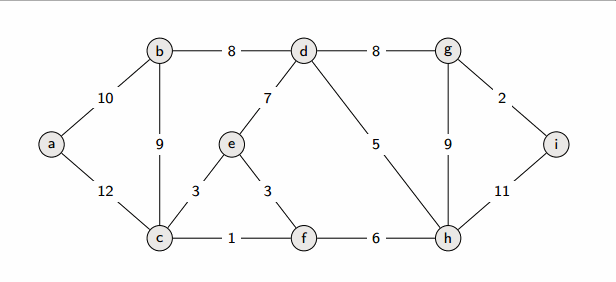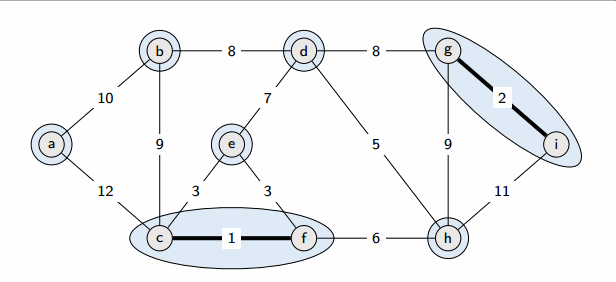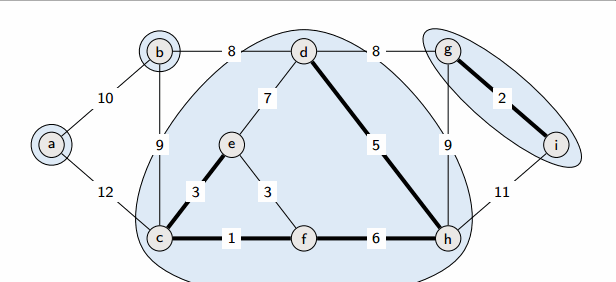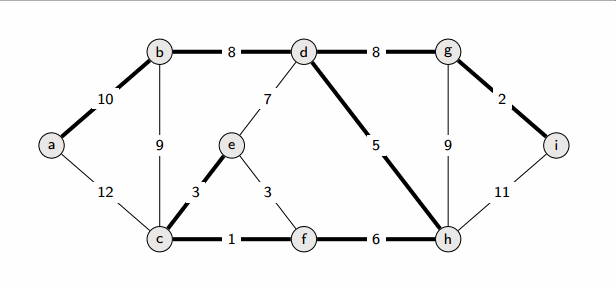
Kruskal 알고리즘
그리디 알고리즘 방식으로, 가장 유리한 간선을 하나씩 선택해 나아가는 방식

• 간선을 하나씩 선택하면서 트리를 완성해나감

[구현 과정]
1. 모든 간선을 가중치에 따라 오름차순으로 정렬
2. 가중치가 낮은 간선부터 선택하면서 트리를 증가
2-1. 만약 해당 간선 선택 시 사이클이 생긴다면, 다음으로 가중치가 낮은 간선 선택
3. n-1개의 간선이 선택될 때까지 2번 반복

[특징]
코드가 간결
but, 간선 리스트 오름차순 정렬이 필요 (n log n) + 간선이 많은 경우 불리함

Prim 알고리즘

• 임의의 정점에서 시작해서 인접 정점 중 최소 비용의 간선이 존재하는 정점을 선택하는 방식
  
• 정점을 하나씩 선택하면서 트리를 완성해나감

[구현과정]
1. 임의 정점을 하나 선택해서 시작
2. 선택한 정점과 인접하는 정점들 중 최소 비용의 간선이 존재하는 정점 선택
2-1. 만약 사이클이 생긴다면 해당 간선 skip
3. 모든 정점이 선택될 때까지 1, 2번 반복

[알고리즘 적용]
1. 각 정점에 대한 체크를 했는지 체크해줘야 하므로 visited 배열을 만들어줌
2. 각 정점에 대한 최소 간선 비용을 저장해줄 minV 배열을 만들어줌
minV[i] = (타 정점 👉🏻 i번 정점) 최소 간선 비용 저장

[특징]
코드가 지저분
but, 간선 정렬 필요없음

사이클이 생겼는지 어떻게 아는데요?

Kruskal 알고리즘

정점이나 간선을 선택할 때마다 서로소 집합 union을 시도 하면서, 같은 부모에 속하는 지 확인하면 됨

Prim 알고리즘

• 정점을 선택할 때마다 visited 배열을 확인해서, 신장 트리에 포함되지 않은 정점인지 체크함
• 신장 트리에 포함되지 않은 정점 중 최소 간선을 갖는 정점을 찾아 연결함