투 포인터, 구간 합

🌈 나동빈 님의 영상을 보고 작성한 글입니다.
https://www.youtube.com/watch?v=rI8NRQsAS_s

투 포인터 (Two Pointers)

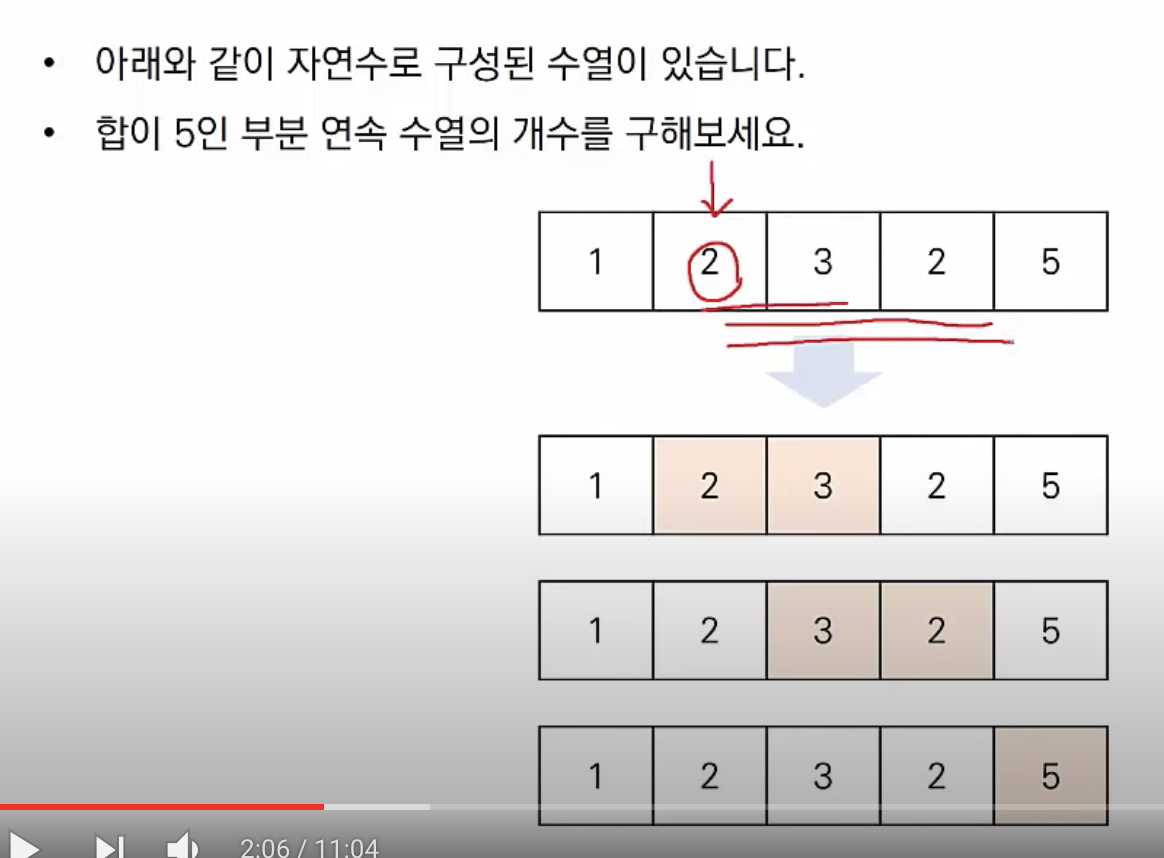
N개의 숫자들 중, 합이 m이 되는 모든 경우의 수를 구하는 문제가 있다.

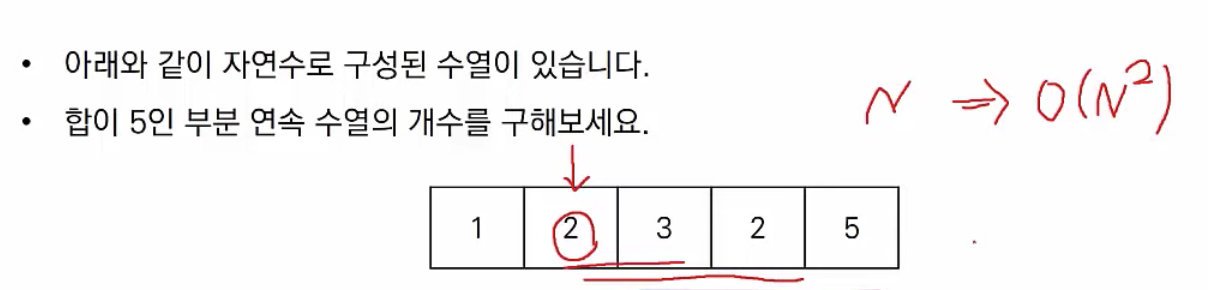
이런 경우 위와 같이 특정 지점에 시작점을 정해서 모든 경우를 고려한다면 O(N^2)의 시간 복잡도를 갖게 된다.
만약 데이터가 백만개라면 무지막지한 시간이 소요되는 것이다.

투 포인터와 이용하면 문제를 O(n) 시간에 해결할 수 있다.

투 포인터 (Two Pointers)

리스트에 순차적으로 접근해야 할 때, 두 개의 점을 이용해 위치를 기록하면서 처리하는 기법

1. 시작점(start)과 끝점(end)이 첫번째 원소의 인덱스를 가리키도록 한다.
2. 현재 부분 합이 M과 같다면 카운트 한다.
3. 현재 부분 합이 M보다 작거나 같으면, end를 1 증가시킨다.
4. 현재 부분 합이 M보다 크다면, start를 1 증가시킨다.
5. 모든 경우를 확인할 때까지 2~4번 과정을 반복한다.

투 포인터 예제 ) [BOJ 2003] 수들의 합 2

n, m = map(int,input().rsplit())
nums = list(map(int,input().rsplit()))

l, r = 0, 0
answer, hap = 0, 0

# l을 차례대로 증가시키며 반복
for l in range(n):
    # r을 가능한만큼 움직이기
    while hap < m and r < n:
        hap += nums[r]
        r += 1
    # 부분 합이 m일 때 카운트 증가
    if hap == m:
        answer += 1
    # m보다 hap이 크거나 같으므로 l 한칸 이동 
    hap -= nums[l]

print(answer)

구간 합 (Prefix Sum)

N개로 이루어진 수열이 있을 때, 주어진 M개의 범위만큼 데이터의 합을 모두 구하는 문제다.
이런 경우 구간 합을 사용하면 O(N+M) 으로 문제를 풀 수 있다.

구간 합 (Prefix Sum)

구간의 합을 여러번 빠르게 구하고자 할 때, 테이블을 만든 뒤 그 테이블을 이용해서 각각의 합을 구하는 기법

1. Prefix Sum을 계산하여 배열 P에 저장한다.
   ✨ P[i]= i번째 인덱스까지의 합
2. 매 M개의 쿼리 정보를 확인할 때, 구간 합은 P[R] - P[L-1]이다.

구간 합 예제 ) [BOJ 11659] 구간 합 구하기 4

import sys
input = sys.stdin.readline

n, m = map(int,input().rsplit())
nums = list(map(int,input().rsplit()))
prefix = [0]
curr = 0

for n in nums:
    curr += n
    prefix.append(curr)

for _ in range(m):
    i, j = map(int,input().rsplit())
    print(prefix[j]-prefix[i-1])