Stanford University CS231n - Lecture 4 :: Backpropagation and Neural Networks
Stanford University CS231n
목록 보기
4/4
Review Last lecture (Lecture 3)

- 모델을 분류하는 방법
1) scores function : w와 x의 값으로 노드의 score 값을 연산
2) SVM loss : score function을 통해서 각 값이 얼마나 특정 클래스에 대해 적합한 결과를 제시하는지 SVM loss function을 통해서 구할 수 있었습니다.
3) 최종 손실 L : data loss(SVM loss혹은 다른 손실함수)의 값과 regularization 값의 합으로 총 손실 값을 의미합니다. 이렇게 Regularization 항을 더해주는 방식은 통해 민감성을 떨어뜨리면 모델을 단순화 시켜 일반화할 수 있도록 도울 수 있습니다.- Optimization : 최적화 방식으로 W에 대한 최적의 기울기를 구할 수 있도록 하는 방법.
- Gradient descent: 기울기를 구하는 방법으로 경사하강법이라고 합니다.
1) Numerical descent: 숫자의 변화를 통해 구하는 수치적으로 구하는 방법. 쉬우나, 오래걸리므로 Analytic descent를 이용해서 값을 구하고 검증하는 방법으로 사용합니다.
2) Analytic descent : 공식을 이요해서 공식을 통해서 구하는 방법입니다. 어렵지만, 빠르고, 정확하므로 gradient값을 구해줄 때 사용합니다.
Backpropagation
기본적인 Node 연산
- 첫 노드에서 입력으로 w와 x값을 받아 벡터연산을 통해 score을 계산해준뒤, hinge loss를 통해서 값을 구해줍니다. 그 뒤, R(w)라는 정규화 항과 데이터 값을 통해 최종 함수 결과 값을 계산해줍니다.
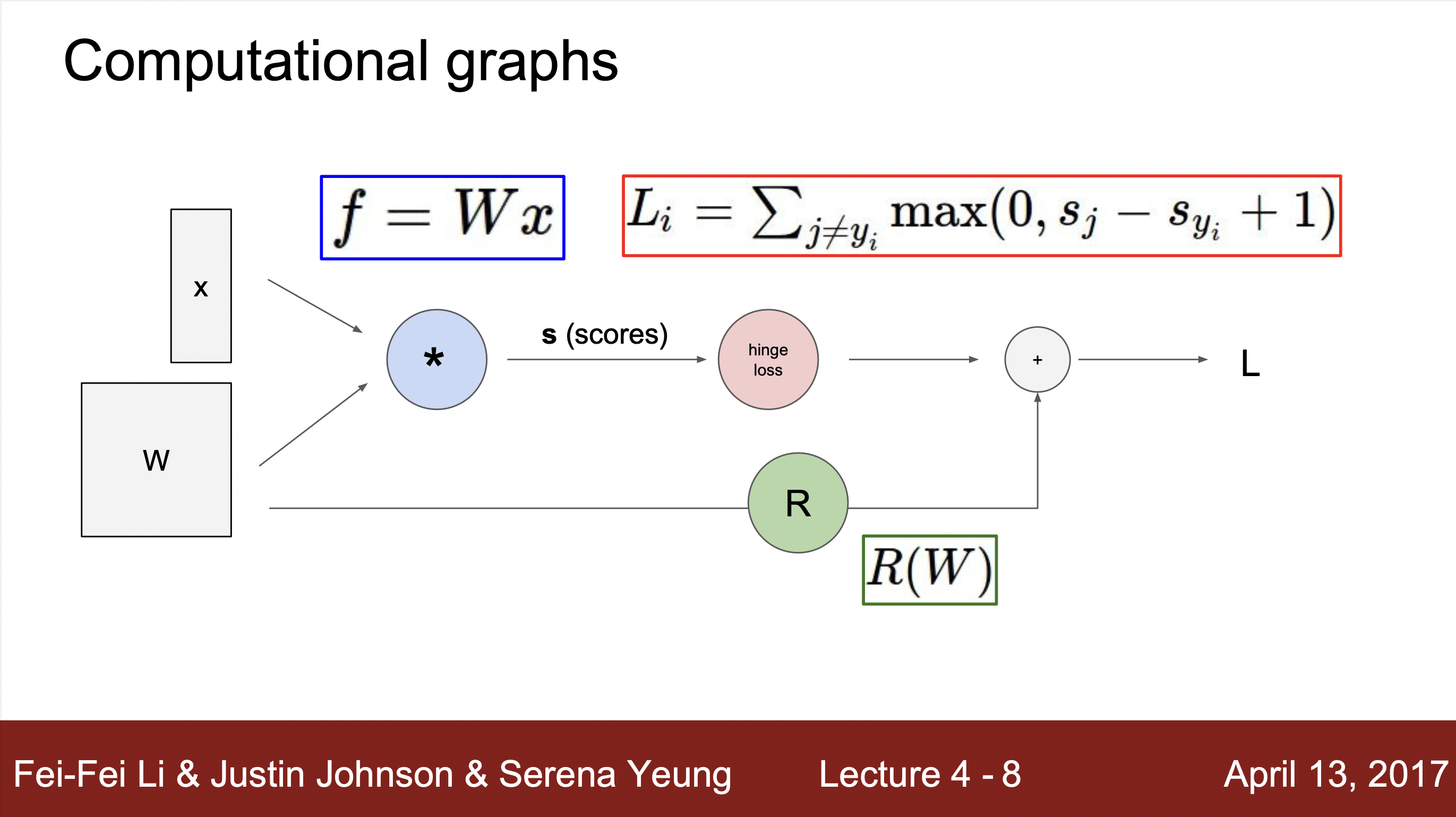
hinge loss : SVM 머신에서 이용되는 손실함수값으로 "최대 마진 분류"에 사용됩니다.
정의 & 사용하는 이유
정의
- 계산 그래프의 모든 변수에 대한 기울기를 구하기 위해 연쇄규칙을 재귀적으로 호출하여 거꾸로 gradient descent값을 구해주는데 이를 Back propagation이라고 합니다.
사용하는 이유 

- 위와 같이 복잡한 모델에서 한번에 계산하기가 힘들고 어려우므로, Back Propagation의 chainrule을 이용하면 간단하게 구할 수 있음 .
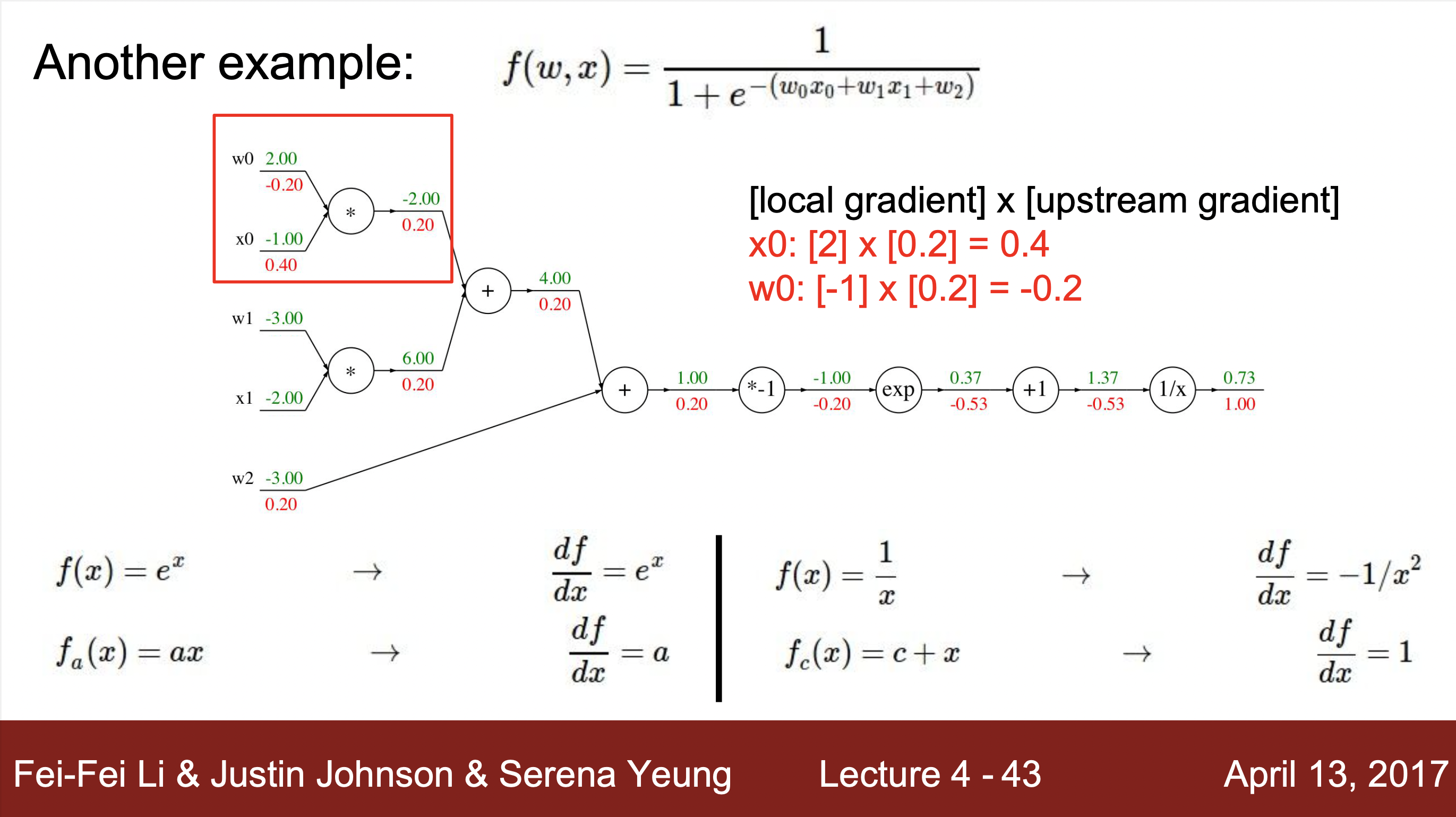
계산하는 방법 예시 : 


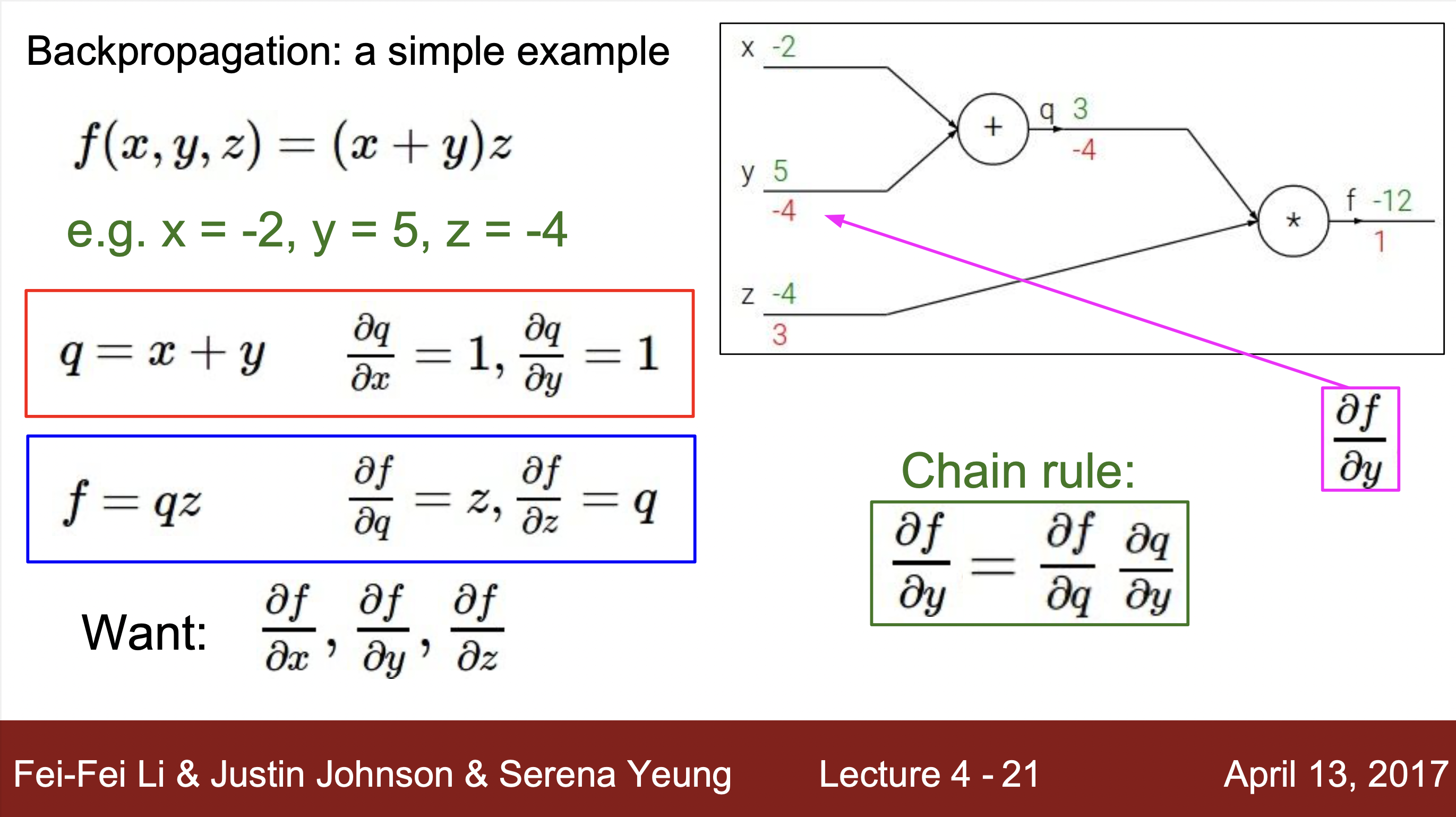
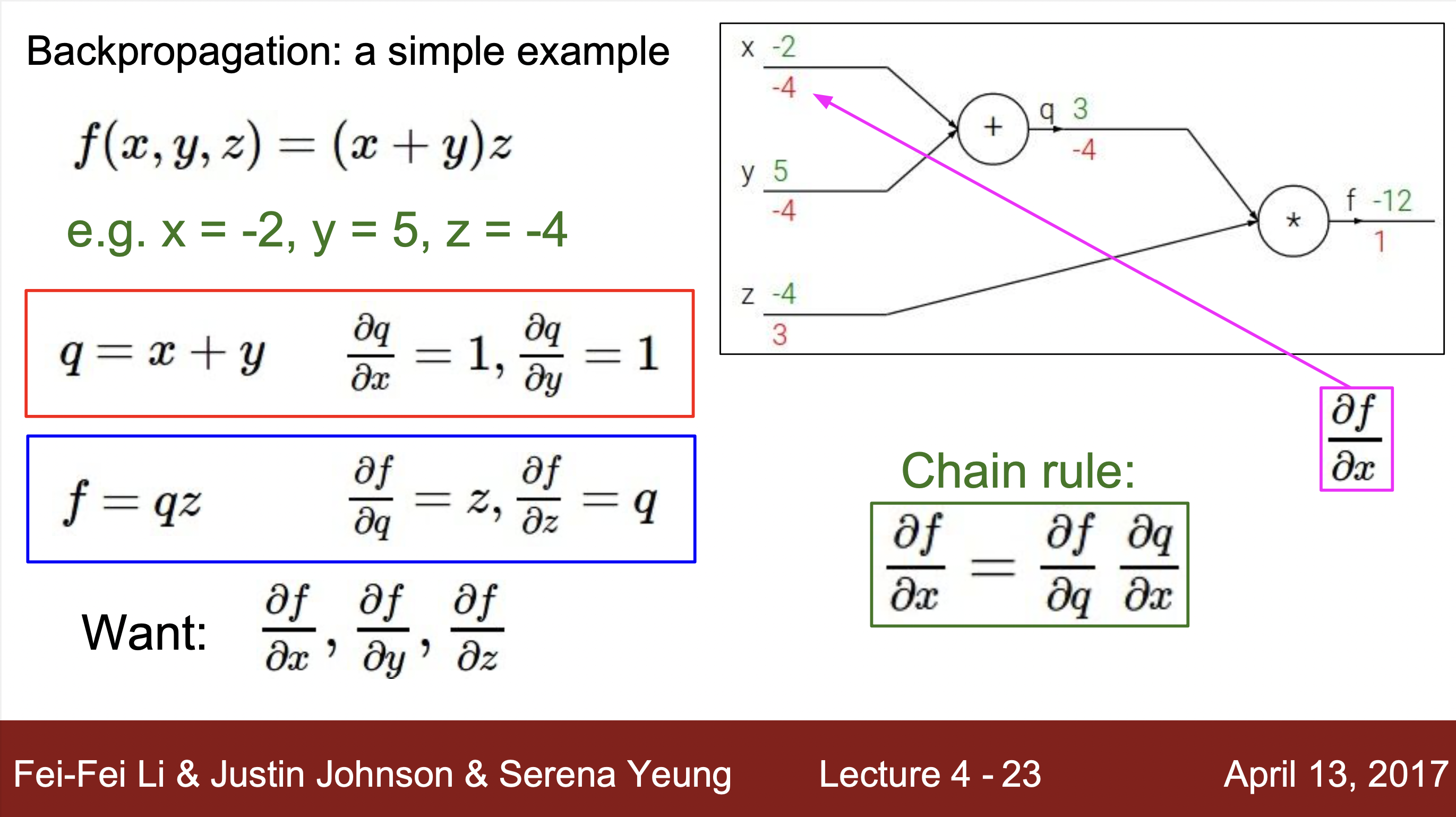
- 예시를 통해 알 수 있는 계산 방법 : 하나의 연산을 하나의 노드로 치환하여 각 연산의 input과 output을 구해주고 해당하는 input과 output의 grdient값을 구해줍니다. 그리고 최종 gradient값과 각 노드에서 구해진 local gradent와의 값과 연산을 통해 최종적으로 값을 최종 값 구해줍니다.
정리
- f = a(x,y)에 해당하는 노드라고 가정했을 때, x와 y에 해당하는 input에 해단 기울기를 output과 함수를 통해 바로 구해줍니다. 이걸 local gradient라고 부르고 역전파현상을 통해서 gradient값이 거꾸로 들어오면 chainRule을 통해서 단순히 local gradient와 upstream gradient값을 곱해줌으로서 최종 결과에 대한 gradient값을 구해줍니다.
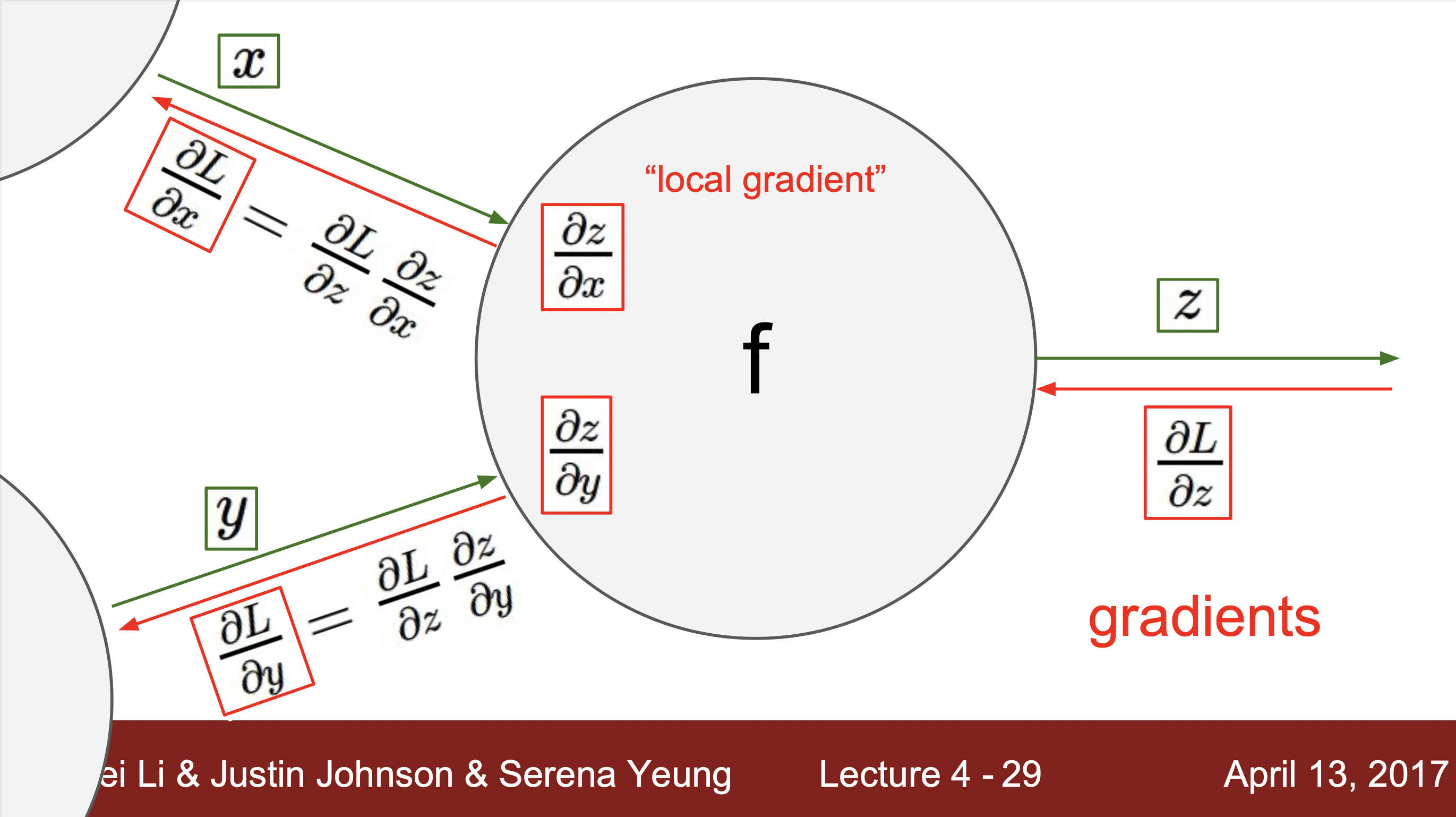
예시 2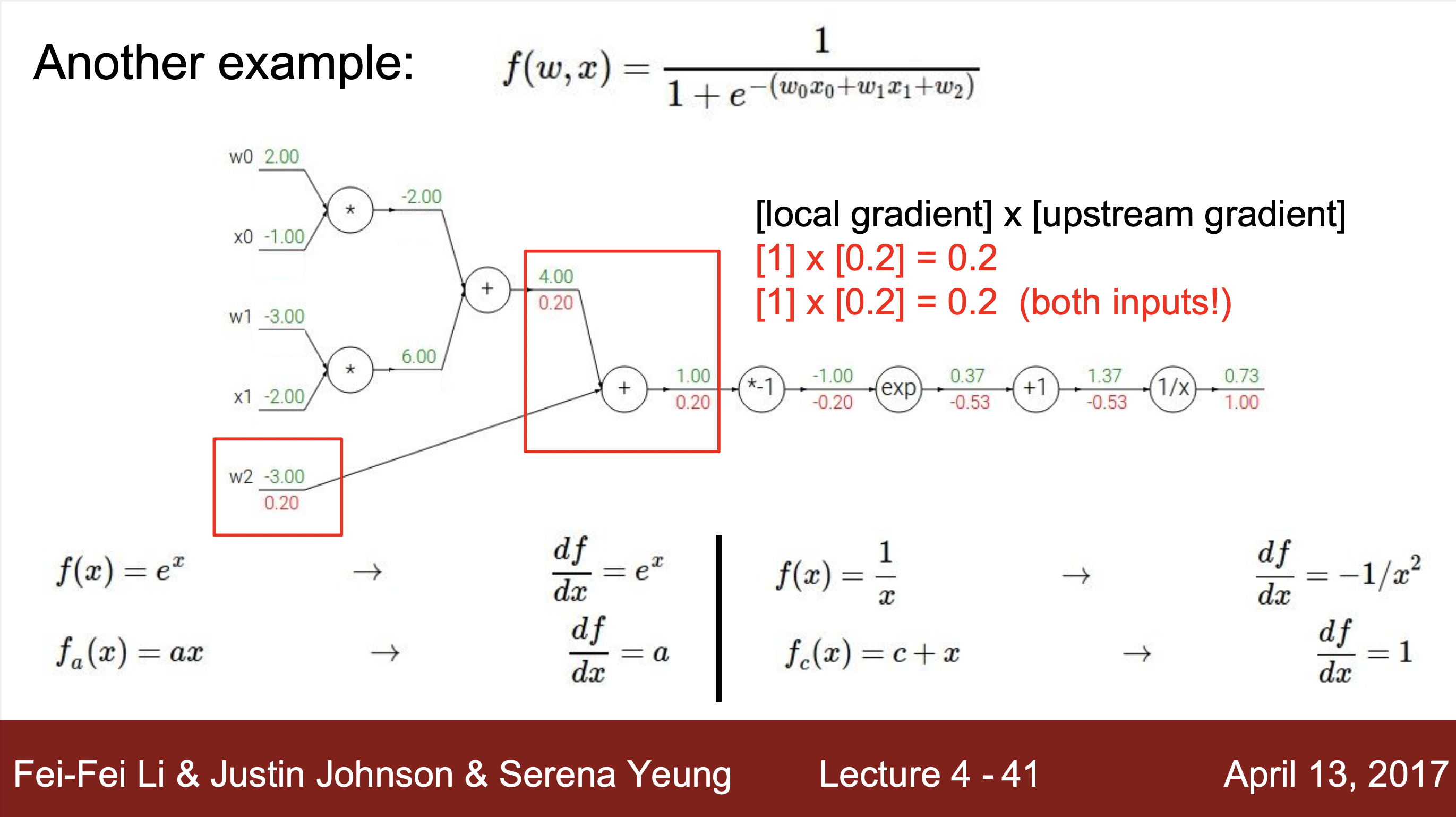
Sigmoid 함수로 보는 연산 Node의 그룹화
- 함수를 연산하는 과정에서 아래와 같이 sigmoid관련한 함수 부분을 연산과정을 해서 다음과 같은 간단한 도함수를 얻을 수 있습니다. 이러한 경우 노드들을 그룹화하여 아래와 같은 노드로 활용할 수 있습니다. 따라서 얼마나 연산을 단순하게 할 것인지, 얼마나 노드 구조를 복잡하게 할 것인지, 노드를 얼마나 복잡하게 만들것인지 개발자가 결정해서 아래와 같이 하나의 노드로 정리를 할 수 있어야 합니다.

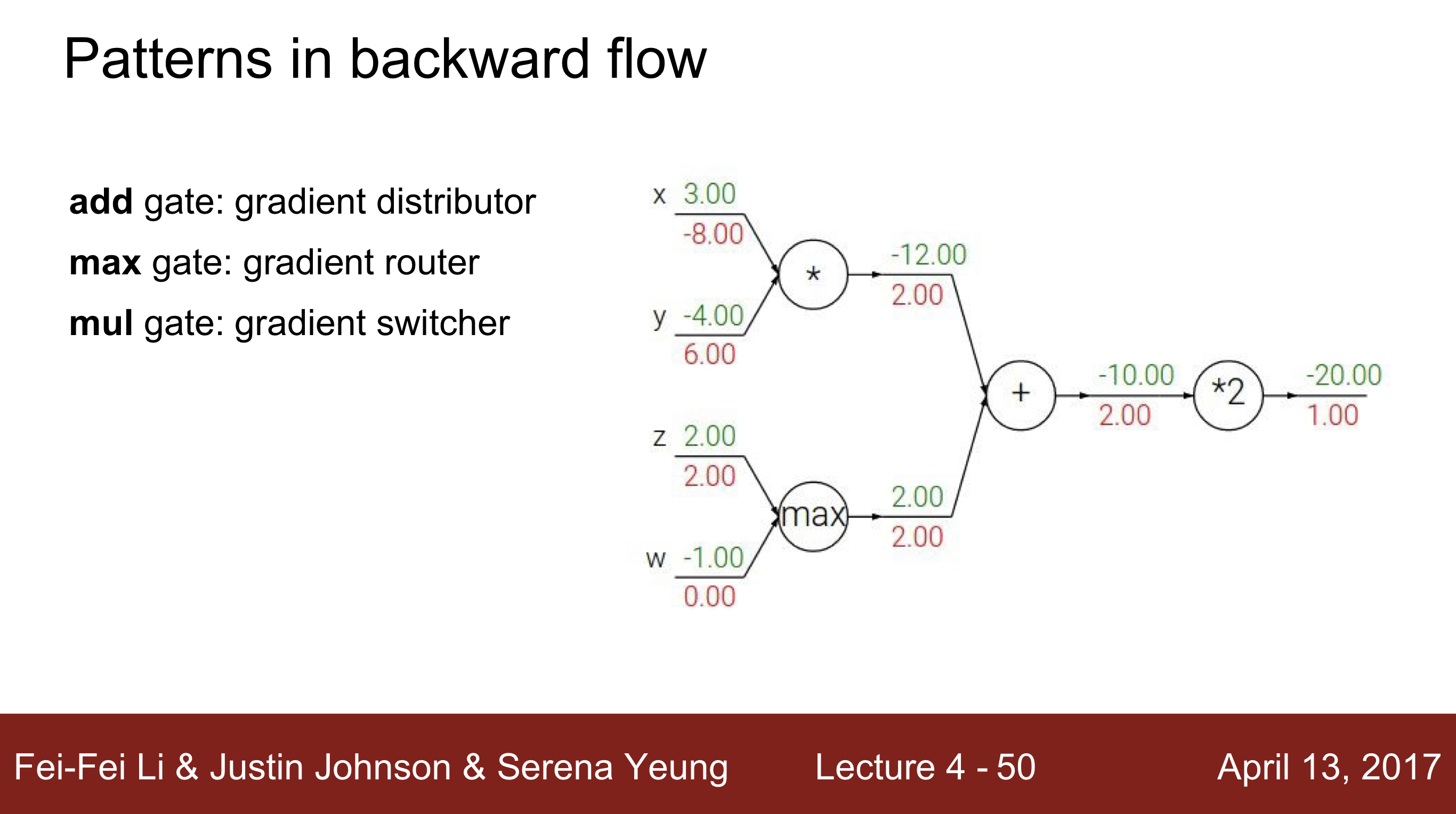
- 연산 게이트들은 아래와 같이 역할을 분류 할 수 있음
- add gate : gradient distributor
게이트를 통해서 갖고있는 동일한 gradient를 각 input에 분배함. - max gate : gradient router
두가지 값중 max의 ouput과 같은 input만 영향을 미치고 있으므로, 한 노드에게 모든 gradient값을 부여한다. 그리고 다른 input의 gradient는 0을 넘겨준다. 한 input만 해당하는 node의 연산에 영향을 준다고 볼 수 있기 때문이다. - mul gate : gradient switcher
Gradient에서 input x1, x2가 있다고 가정할 때, x2의 gradient는 x1의 값이 scale이 되어, x2의 gradient는 x1의 값이 scale이 되어 전달되어 gradient switcher라고 합니다.
- add gate : gradient distributor
- 두개의 output에서 하나의 input으로 Backpropagation하는 경우
- 모든 gradient의 값이 input으로 더해져서 넘겨집니다. 이러한 경우, 서로의 모든 노드들이 값이 변할 때마다 다 영향을 준다고 생각을 하시면 됩니다.
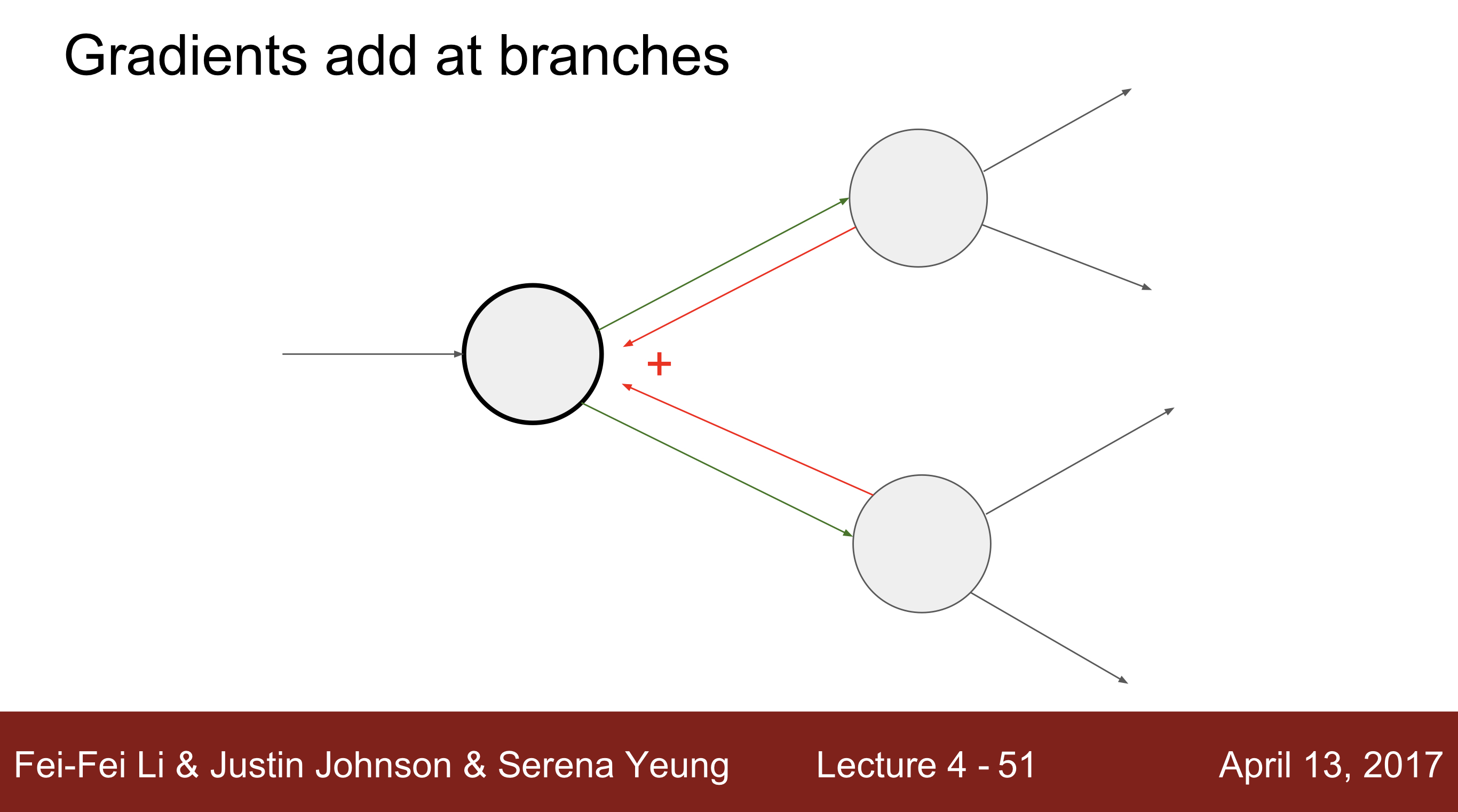
- 모든 gradient의 값이 input으로 더해져서 넘겨집니다. 이러한 경우, 서로의 모든 노드들이 값이 변할 때마다 다 영향을 준다고 생각을 하시면 됩니다.
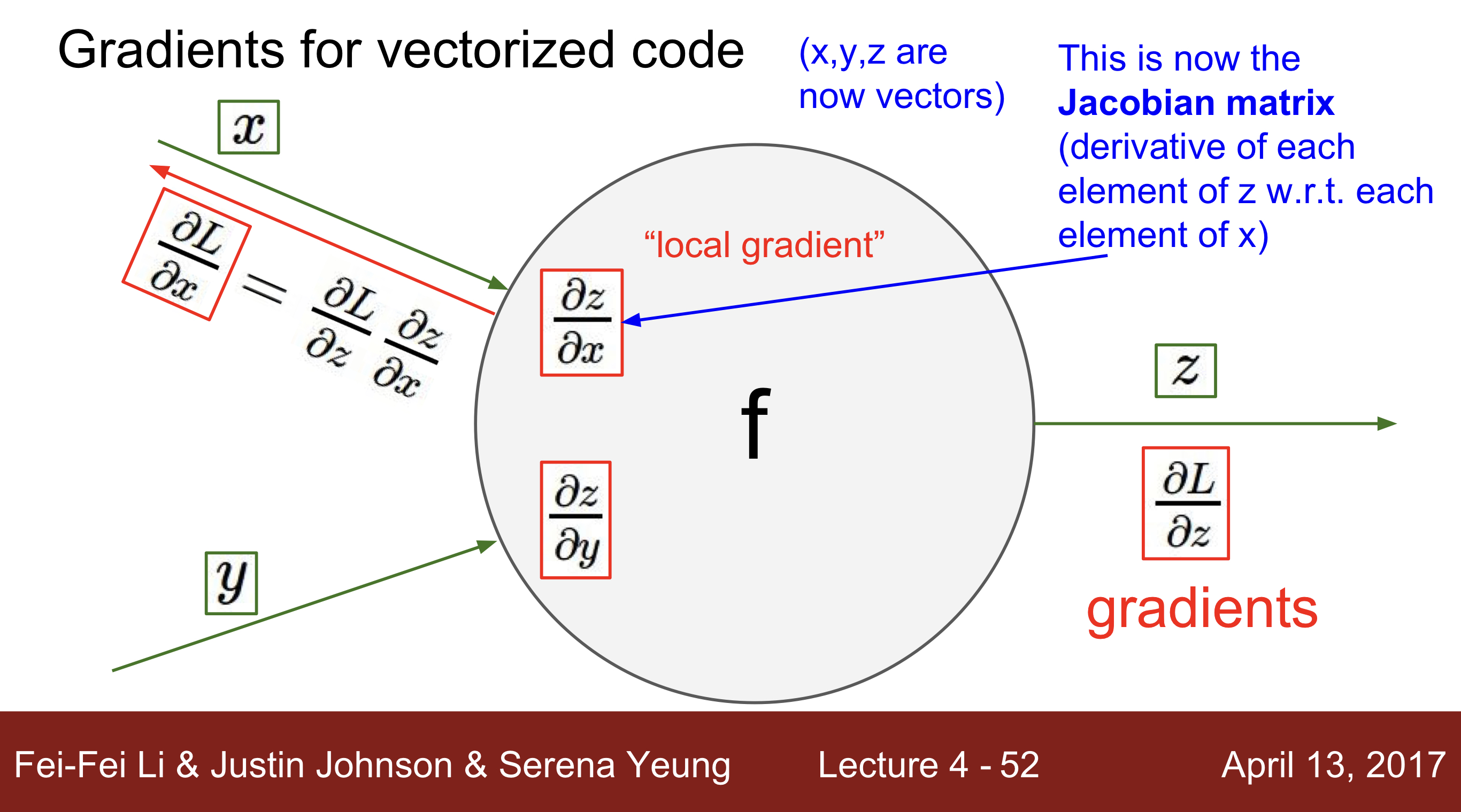
Vector Gradient 연산
- Gradient for Vectorized Code. : Jacobian matrix
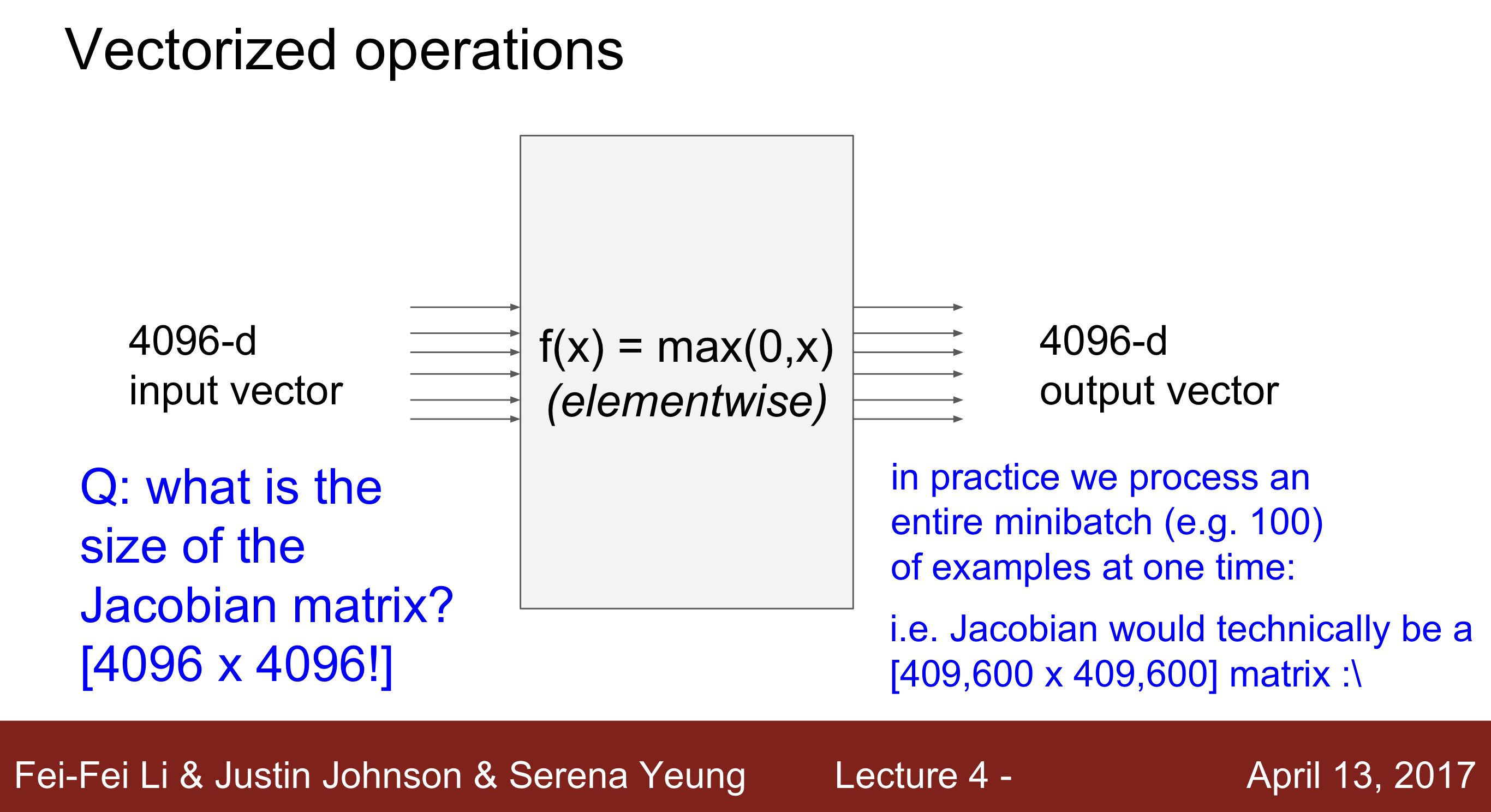
- Ex) f(x) = max(0,x)
Q1 : what is the size of the matrix? 1개의 cell에서 vector의 크기는 input X output의 크기 4096 X 4096 이라고 볼수 있다.
Q2 : What does it look like ? 사실상 하나의 값만 계산을 해주는 식이기 때문에 대각행렬로 나타나게 된다.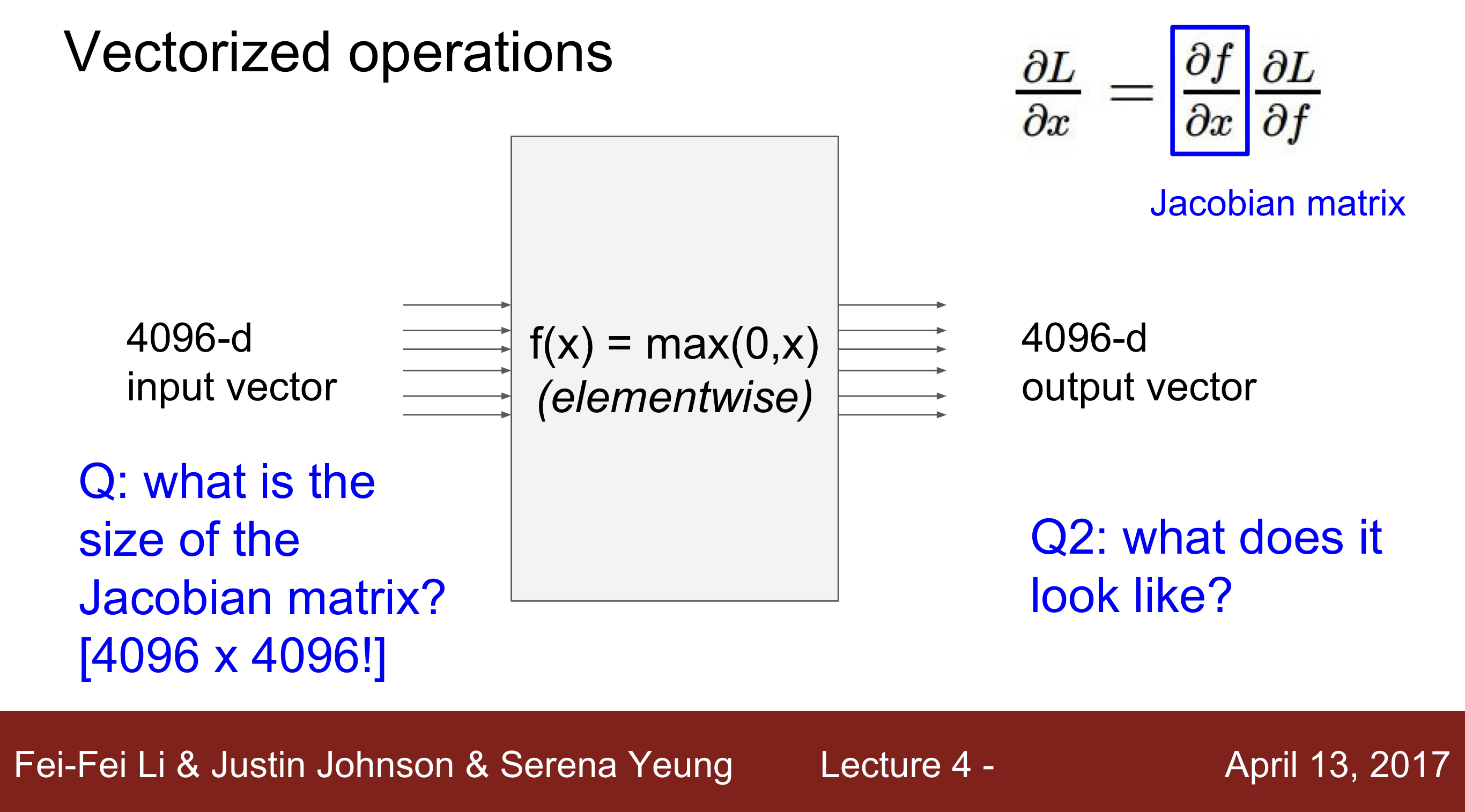
- Ex 2)


- Ex) f(x) = max(0,x)
- Caffe Layers라는 예시를 통해서 안에 있는 layer에서 각 gradient 벡터의 산을 확인할 수 있음. Ex) sigmoid layer에서 sigmoid관련 연산을 찾아볼 수 있음. 이외에도 layer에 있는 코드를 보면서 확인 가능

Backpropagation Summary
- 인공신경망은 사실상 매우 커서 한번에 공식을 통해 gradient를 구해주는 것은 매우 어려운 일이다. 이를 해결하기 위해 나온 방법이 BackPropagation이다.
- Backpropagation : 신경망 구조를 따라 재귀적인 chain rule을 이용해서 모든 변수들의 gradient를 계산해주는 방법이다.
- 구현하는 과정에서 구조를 유지하기 위해 forward()/ backward() API를 이용한다.
- forward : compute와 operation의 결과를 저장하는 방식으로 진행돔
- backward : chain rule을 적용하여 모든 셀의 gradient를 구해줌.
- 이 과정에서 optimization이 쓰이며 그 과정을 토해 정확한 W의 값을 구하게 됨.

Neural Networks
Neural Networks : without brain stuff
- 해당 layer을 더 깊게 깊게 만들수록, 단일 템플릿이 아닌 여러 템플릿에 대한 클래스 분류를 할 수 있어짐.
Ex) 만약 빨간 차를 분류할 수 있는 모델을 1 layer로 분류를 할 수 있다고 가정을 했을 때, 이 분류기는 노란차를 분류할 수 없다. 반면 2 layer로 만든다면, 나온 결과 값들을 다시 한번 재공정을 하는 과정을 거치기 때문에, 노란차, 빨간차 모두 자동차로 인식할 수 있게 된다. 즉 단일 layer보다 multiple-layer가 템플릿을 구분할 수 있는 성능이 올라간다.

Neural Network
- Brain Neural Network 는 Impulse(자극)이 dendrite으로 들어오고, 이 값을 다양한 연산을 통해 cell body로 전해지고 다른 셀로 전달됩니다. 그리고 이러한 방식처럼 인공신경망도 구성이 되고, input을 받고 연산을 통해 activation function에 전달되고 이 값이 특정한 값 이상이 되면, 값이 전달될 수 있도록 구현되어 있습니다.
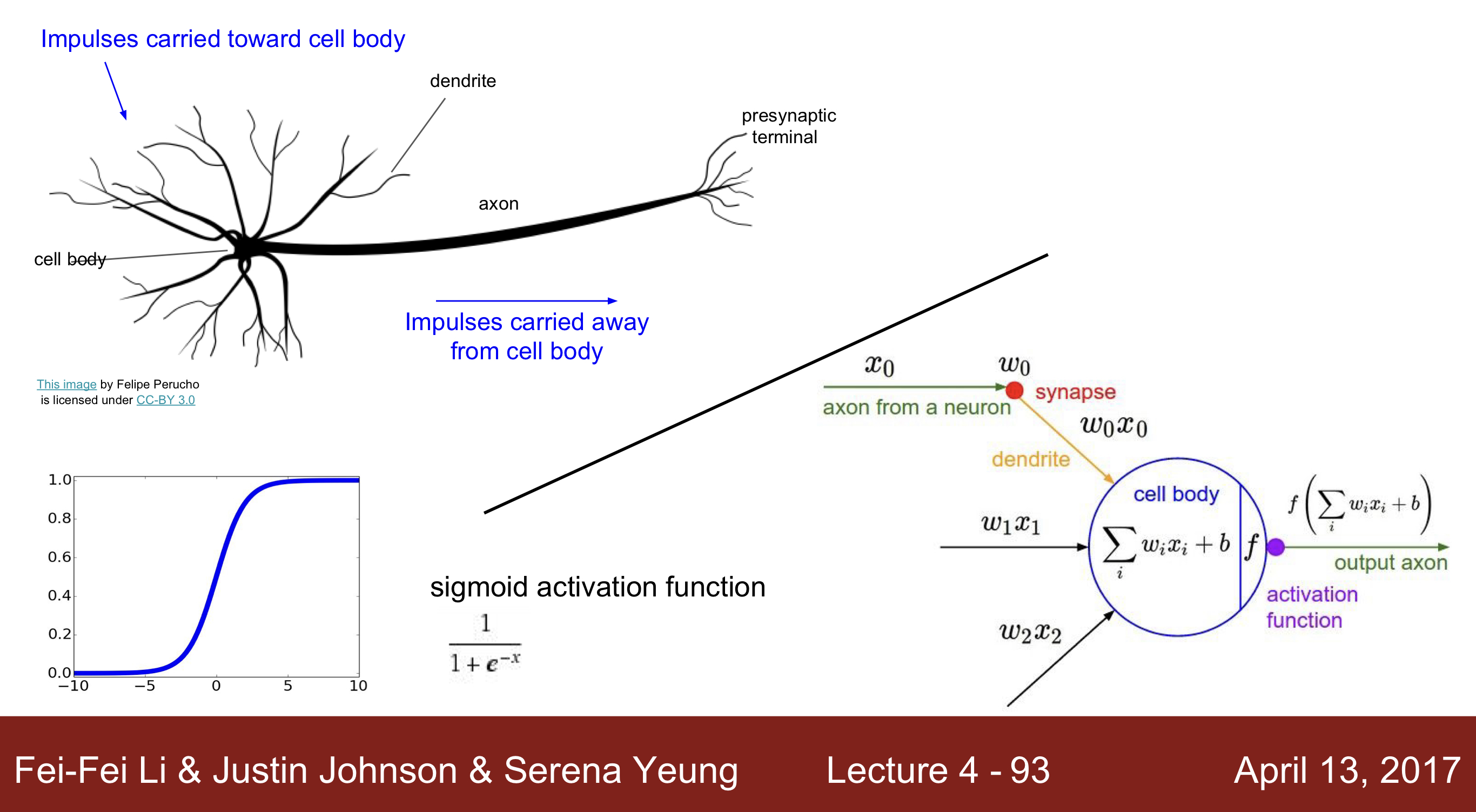
- 하지만 실제 인공신경망의 신경은 매우 다양한 타입이 존재하며, 많은 non-linear 방식의 문제도 계산할 수 있습니다. 또한 뉴런이 더 다양한 방식으로 계산하기도 합니다. 그래서 유사성이 존재한다는 것이지, 완벽히 같다고 볼 수 없습니다.

- Activation function의 종류 : sigmoid, Leaky ReLu, tanh, Maxout, tanh, ReLU, ELU

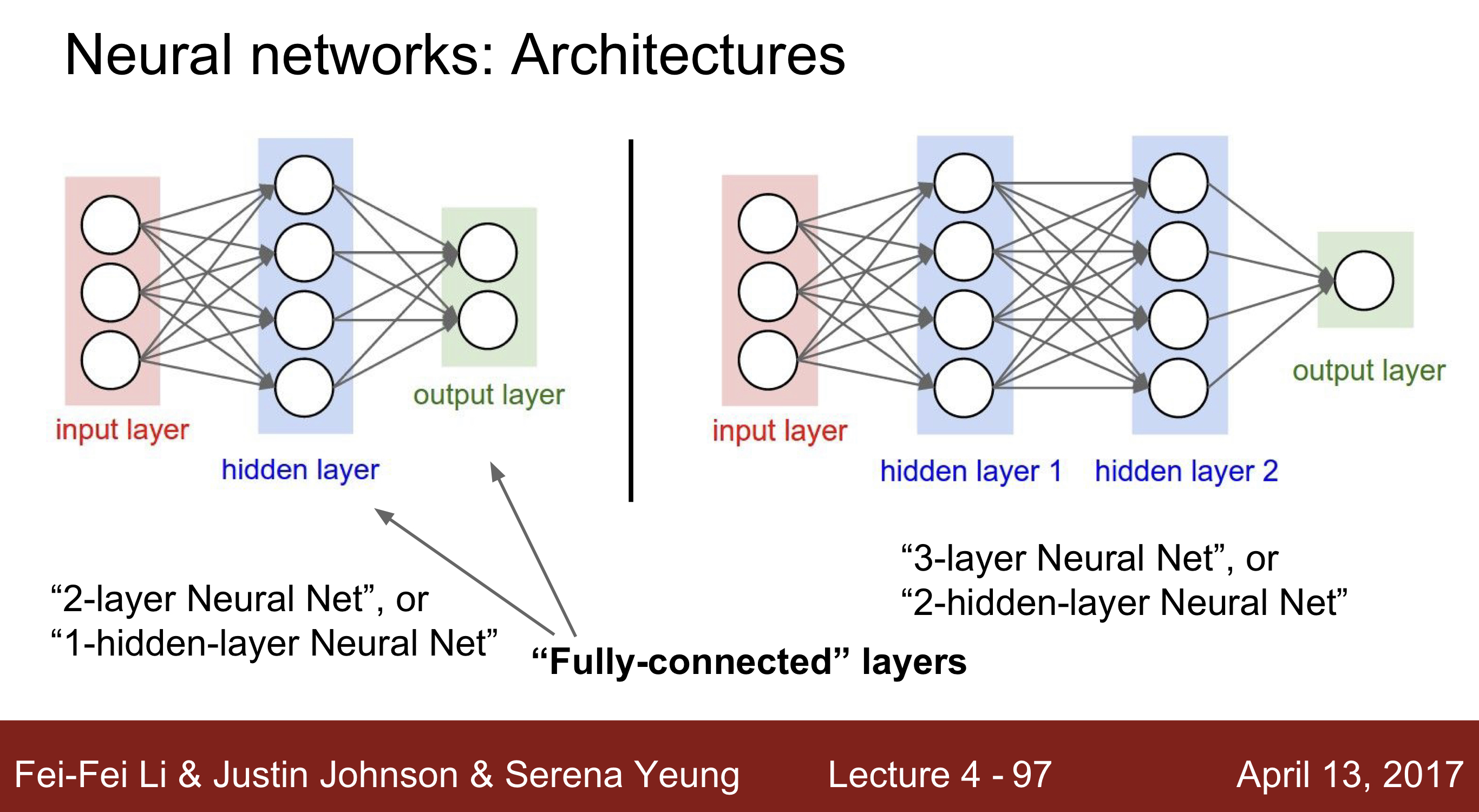
- Neural Network : K개의 Fully connected layer는 다음 방식처럼 불림
K - layer Neural Net( (K-1)-hidden-layer-Neural -Net)
강의자 : Serena Yeung ( Fei-Fei Lab 박사과정)
출처 : Stanford University School of Engineering
Lecture 4 | Introduction to Neural Networks
