https://leetcode.com/problems/maximal-rectangle/
1과 0으로된 2차원 리스트에서 가장 큰 직사각형을 구하는 문제이다.
코드 1 - 실패
처음에는 BFS로 연결된 점의 집합을 구한 뒤에 각각 x와 y들의 차가 최소인 지점을 찾으면 만족하는 직사각형이 되겠거니 했다.
from collections import defaultdict
class Solution:
def maximalRectangle(self, matrix: list[list[str]]) -> int:
r = len(matrix)
c = len(matrix[0])
dy = [0, 0, 1, -1]
dx = [1, -1, 0, 0]
ans = 400000000
for i in range(r):
for j in range(c):
if matrix[i][j] == "1":
matrix[i][j] = "0"
que = [(i, j)]
xs = defaultdict(list)
ys = defaultdict(list)
idx = 0
xs[j].append(i)
ys[i].append(j)
while idx < len(que):
y, x = que[idx]
idx += 1
for d in range(r):
ny = y + dy[d]
nx = x + dx[d]
if 0 <= ny < r and 0 <= nx < c and matrix[ny][nx] == "1":
matrix[ny][nx] = "0"
que.append((ny, nx))
xs[nx].append(ny)
ys[ny].append(nx)
minX = 4000
minY = 4000
for x in xs.values():
minX = min(max(x) - min(x) + 1, minX)
for y in ys.values():
minY = min(max(y) - min(y) + 1, minY)
print(minY * minX, minY, minX, que)
ans = min(ans, minY * minX)
return ans
그런데 문제의 첫 번째 테스트케이스부터 실패했다.
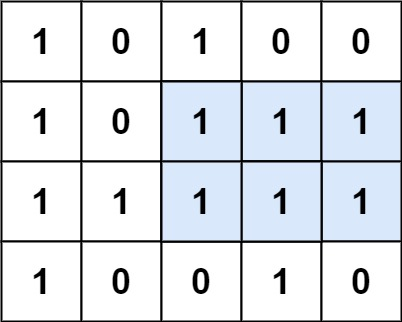
첫 번째 테스트케이스로 내 코드가 구한 답은 3이다.
y의 최소 길이는 2번 행만 해당하는 1이되고, x의 최소 길이는 2~4번 열이 해당하는 3이 된다.
그런데 정답은 색이 칠해진 6이다.
DP로 할까 하다가 더 편한 BFS로 될 것 같아서 시도했는데 실패하고 말았다.
코드 2
솔루션 중에 히스토그램처럼 접근한 swift코드가 있어서 참고했다.
r = len(matrix)
c = len(matrix[0])
heights = [0] * (c+1)
ans = 0
for row in matrix:
for j in range(c):
if row[j] == "1":
heights[j] += 1
else:
heights[j] = 0필요한 값을 정의하고, 히스토그램의 높이를 저장할 height라는 리스트를 정의한다. 이때, 오른쪽에서 왼쪽으로 너비를 측정하므로 가장 마지막 원소를 포함시키기 위해서 0을 추가해준다.
행을 돌면서 1인 경우에는 height에 1을 더해주고, 0이면 이때까지 쌓인 높이가 초기화가 됐기에 0을 저장한다.
stack = []
for j in range(c+1):
while stack and heights[j] < heights[stack[-1]]:
last = stack.pop()
height = heights[last]
width = j - 1 - (stack[-1] if stack else -1)
ans = max(ans, height * width)
stack.append(j)x좌표를 저장할 stack이라는 리스트를 선언한다.
그리고 height를 순회하는데 만약 stack이 비어있다면 추가해준다.
heights[j]가 stack에 마지막으로 저장된 높이보다 작으면 스택에 마지막으로 저장된 높이를 기준으로 직사각형의 너비를 계산한다.
너비는 j직전까지는 height[last]의 높이를 가졌을 것이기에 j-1부터 측정한다.
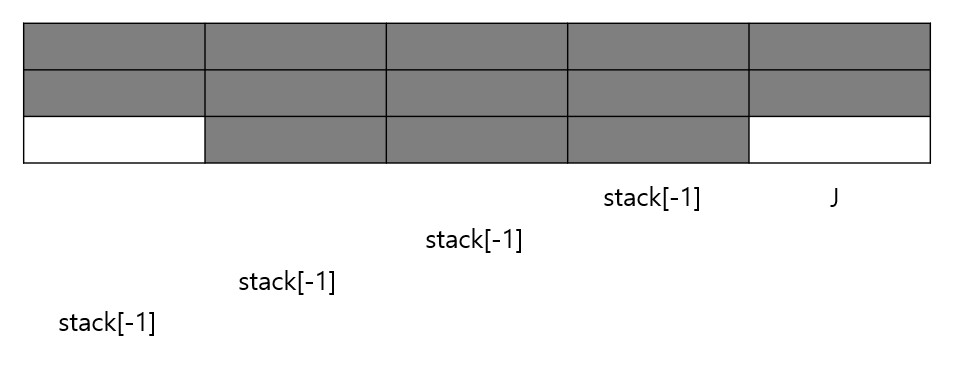
만약 stack에 다른 값이 있다면 해당 x좌표의 높이는 heights[last]보다 작을 것이기에 x좌표까지 측정하고, 만약 값이 없다면 왼쪽 끝까지 측정한다.
매번 너비를 계산할 때마다 최대 너비를 비교해서 업데이트 해주면 답을 구할 수 있게 된다.
from collections import defaultdict
class Solution:
def maximalRectangle(self, matrix: list[list[str]]) -> int:
r = len(matrix)
c = len(matrix[0])
heights = [0] * (c+1)
ans = 0
for row in matrix:
for j in range(c):
if row[j] == "1":
heights[j] += 1
else:
heights[j] = 0
stack = []
for j in range(c+1):
while stack and heights[j] < heights[stack[-1]]:
last = stack.pop()
height = heights[last]
width = j - 1 - (stack[-1] if stack else -1)
ans = max(ans, height * width)
stack.append(j)
return ans
코드를 이해하는데 한참이 걸렸다. 파워포인트로 끄적이고 해보니 대충 이해가 가긴 했는데 표시해두고 나중에 다시 풀어봐야겠다.
