드디어 국기 훈련에 개임 개발을 위한 고등 수학 부분이 나왔다.
인터넷 강의로 들을 때부터 예상이 가긴 한 일이긴 하다.
본래라면 고등학교 때 다 배우는 내용일 지도 모르지만, 고1 때부터 웹 프로그래밍에 올인하느라 정규 수업을 건너뛴 나에게는 큰 장애물이었다.
다행히 인강과 국기 훈련이 도움이 됐다.
벡터는 좌표값으로 표기하며 0,0을 기준점으로 해당 좌표를 잇는 선을 그렸을 때 그 선의 방향과 길이를 벡터의 방향과 힘(F, Magnitude)이라고 한다.
벡터의 개념에 대해서는 전부터 알고 있었다. 2차원과 3차원의 개념에 대해서만 이해하고 있으면 그다지 어려운 개념도 아니고, 이건 상식이니깐.
문제는 벡터의 연산들이었다.
게임 프로그래밍에서 중요한 벡터의 연산은
- 벡터의 힘(매그니튜드)값 구하기
- 벡터 합, 차
- 벡터 스칼라 곱
- 벡터의 정규화
- 벡터 내적, 외적
이 정도다
벡터의 매그니튜드값 구하기
2차원으로 그리면 이해가 쉽다.
피타고라스의 정리(직각 삼각형의 밑변^2 + 높이^2 = 빗변^2)는 중학교 수준에서 배우니까.
그림으로 그리면 아래와 같다.
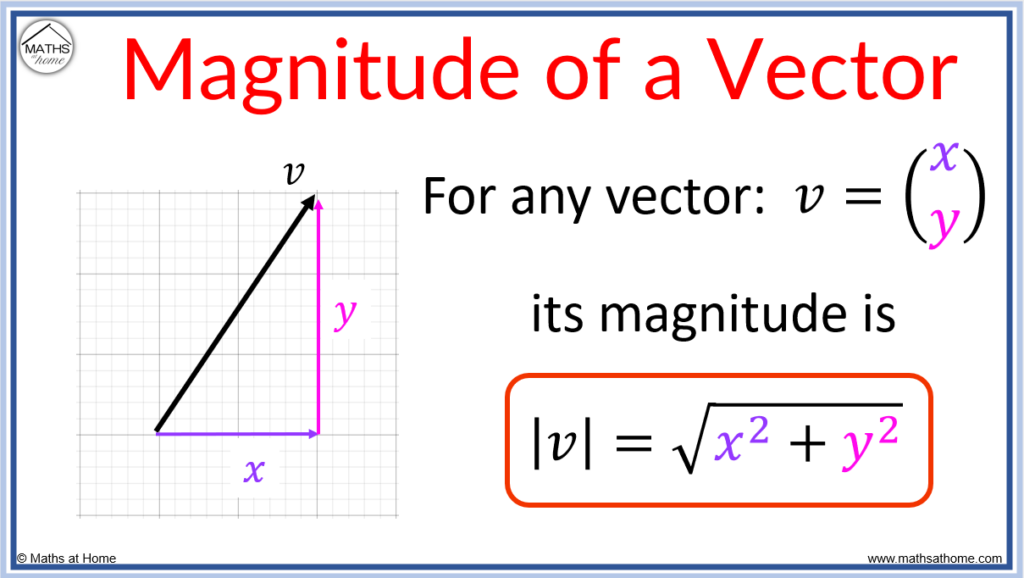
2차원 벡터에서 매그니튜드 값 = 루트(x^2+y^2)
3차원 벡터에서의 값은 이미지를 봐도 직관적으로 이해가 안가지만 일단 공식은 비슷하다.
3차원 벡터의 매그니튜드값 = 루트(x^2 + y^2 + z^2)
벡터의 합, 차
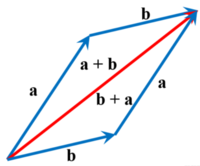
벡터의 합은 단순하다 벡터 V1와 벡터 V2가 있다고 했을 때 벡터 V1의 좌표를 기준으로 V2만큼 더 이동하면 된다.
단순히 공식으로는
V1(x1, y1), V2(x2, y2)일때
두 벡터의 합 V는 V(x1 + x2, y1 + y2)
3차원 벡터일 때도 동일하며 벡터의 차도 - 로 바꿔줘야 한다는 것 말고는 동일하다.
벡터 스칼라 곱
스칼라 곱은 벡터와 숫자를 곱하는 것으로 벡터의 각 성분에 숫자를 곱한다
V(x, y)가 있고 여기에 스칼라 a 를 곱한다면 결과는 V(x a, y a)가 된다.
정규화
정규화는 벡터의 매그니튜드 값이 1이 되도록 각 성분을 매그니튜드값으로 나누는 것을 말한다.
벡터를 정규화 시켜두면 방향은 같되 특정 매그니튜드 값을 가지는 벡터를 만들기 쉬워진다.
벡터의 내적(Dot)
두 벡터가 가르키는 방향의 차이를 연산으로 구한다.
결과 값으로 스칼라 값이 나오게된다.
게임 프로그래밍에서는 두 벡터가 가지는 차이를 통해 적이 오른쪽에 있는지 왼쪽에 있는 지를 판별하는 지 등을 구현하는데 사용할 수 있다.
V1(x, y1), V2(x2, y2)
V1ㆍV2 = V(x1 x2 + y1 y2)
내적의 결과는 두 벡터의 크기 사이각의 연산과 같다.
V1ㆍV2 = ||V1|| ||V2|| cos a
3차원에서도 2차원과 거의 동일하다.
벡터의 외적(Cross)
3차원 벡터에서 두 벡터를 각각 변으로 가지는 면에 수직한 벡터(일명 법선!)을 구하는 연산이다.
연산의 원리에 대해서는 행렬 계산에 대한 이해가 필요한데.. 여기에 대해서는 학원 과정에서도 스킵한 관계로 나도 스킵하고 기록한다.
그냥 이런 식으로 계산한다고 알고만 있어두자
V1(x1, y1, z1), V2(x2, y2, z2)
V1 x V2 = (y1 z2 - z1 y2, z1 x2 - x1 z2, x1 y2 - y1 x2)
