[백준 9663]백트랙킹 N-Queen

may.log·2023년 4월 15일

백준

백트랙킹이란?

백트랙킹은 알고리즘 기법 중 하나로, 재귀적으로 문제를 하나씩 풀어가되, 현재 재귀를 통해 확인중인 노드(상태)가 제한 조건에 위배되는지(유망하지 않은지) 판단하고, 그러한 경우에는 해당 노드(상태)를 제외하고 다음 단계로 나아가는 방식이다.

여기서 중요한 점은 특정 노드(상태)를 제외한다는 것이다!
백트랙킹은 현재 상태(노드)에서 다음 상태(노드)로 나아갈 수 있는 모든 경우를 찾되, 그 중 유망하지 않다면 현재에서 더 이상 나아가지 않고 이전의 상태(노드)로 돌아가 다음 상태(노드)를 검사한다.
백트랙킹을 사용하는 알고리즘 중 하나는 대표적으로 DFS가 있다. DFS는 재귀를 통해 가능한 경로 중 유망한 경로만 찾아서 탐색한 뒤 다시 돌아와 그 중 가장 최적의 경로를 반환한다.
백트랙킹을 사용해 해결할 수 있는 문제는 의사 결정, 최적화, 열거하기 등이 있다.
사실 백트랙킹은 사용 가능한 경우가 많지만 시간 복잡도가 보통 Exponential(지수, 2^n 꼴)이며, 대부분 Dynamic Programming, 그리디 알고리즘 등으로 더 빠르게 해결할 수 있다.
하지만 일부 문제들은 여전히 백트랙킹으로만 해결이 가능한 문제도 있다..!

백트랙킹 사용 예

문제

N-Queen 문제는 크기가 N × N인 체스판 위에 퀸 N개를 서로 공격할 수 없게 놓는 문제이다.

N이 주어졌을 때, 퀸을 놓는 방법의 수를 구하는 프로그램을 작성하시오.

입력

첫째 줄에 N이 주어진다. (1 ≤ N < 15)

출력

첫째 줄에 퀸 N개를 서로 공격할 수 없게 놓는 경우의 수를 출력한다.

문제 정의

각 행당 하나의 퀸이 놓인다.
다음 행에 놓일 퀸의 위치는 백트랙킹 방법을 이용한다.

첫번째 행에 퀸을 놓는다.
두번째 줄에 되는 칸이 있으면, 세번째 줄로 내려간다.
세번째 줄에 되는 칸이 없으면, 다시 두번째 줄로 올라간다.
이때, 이전 행에 놓인 퀸들과 같은 열에 놓여있는지와 같은 대각선상에 위치하는지 체크해야한다.
여기서 같은 대각선상 이란 (1)왼쪽아래에서 오른쪽 위로의 방향, (2)왼쪽위에서 오른쪽 아래로의 방향을 말한다.
row == n 은 각 행당 퀸이 모두 놓인 경우이므로, sum+=1을 해준다.
처음에 2차원 배열을 이용했지만,
arr 배열에서의 인덱스를 행과 대응, 인덱스를 값에 대응하면 1차원 배열으로도 풀 수 있다!
ex) arr[3]=2 : 3번째행의 2열에 퀸이 놓여있다.
- 백트래킹은 재귀함수를 사용한다.
- 함수를 이용하자!

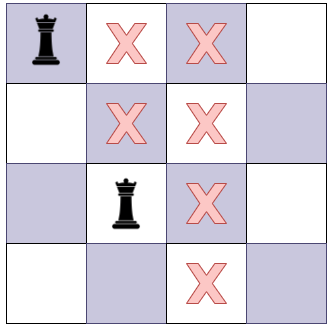
위 사진에서는 3번째 열에서 어떠한 곳에서든 퀸을 배치할 수 없다! 그러니 백트랙킹으로 2번째 열로 돌아가 다시 다른 행에 배치한다.

코드1

import sys
n = int(sys.stdin.readline())
arr=[0 for _ in range(n)]
sum=0

def check(r1, c1, r2, c2):
	if c1==c2:
    	return True		# 같은 열
    if r1-c1=r2-c2:
    	return True 	# (1)번 대각선
    if r1+c1=r2+c2:
    	return True		# (2)번 대각선
    return False

def dfs(row):
	if row==n:
    	global sum
    	sum+=1
    else:
    	for cand in range(n):	# row행에 퀸이 놓일 열을 순차적으로 탐색
        	possible=True
            for i in range(row):	# row이전 행들에 놓인 퀸에 대해서 열, 대각선 체크
            	if check(row, cand, i, arr[i]):
                	possible=False
                    break
            if possible:
            	arr[row]=cand
                dfs(row+1)
                arr[row]=0
 dfs(0)
 print(sum)

코드2

import sys
n = int(sys.stdin.readline())
arr = [0 for _ in range(n)]
sum = 0

def check(row):
	for i in range(row):
    	if arr[row]==arr[i] or abs(arr[row]-arr[i])==abs(row-i):	# 같은 열, 대각선 (1), 대각선 (2) 이면,
        	return False
    return True

def dfs(row):
	if row == n:
    	global sum
        sum+=1
    else:
    	for cand in range(n):	# row행에 퀸이 놓일 열을 순차적으로 탐색
			arr[row]=cand	#행 값 고정
            if check(row):
            	dfs(row+1)

코드1,2 모두 python3으로 제출하면 시간초과 발생,,
pypy3로 제출해야 함.

다른 백트랙킹 문제

The knight's tour problem (https://www.geeksforgeeks.org/the-knights-tour-problem/)
Rat in a Maze (https://www.geeksforgeeks.org/rat-in-a-maze/)
Subset Sum(https://www.geeksforgeeks.org/subset-sum-problem/)
m Coloring Problem(https://www.geeksforgeeks.org/m-coloring-problem/)

DFS와 백트랙킹(Backtracking)의 차이

DFS는 기본적으로 그래프 형태 자료구조에서 모든 정점을 탐색할 수 있는 알고리즘 중 하나이다.
깊이를 우선으로 탐색하기에 재귀 또는 스택을 이용한다.
재귀를 이용해 탐색을 수행한다는 부분에서 완전탐색 알고리즘에서의 재귀/백트랙킹과 유사한 측면이 보여 혼란이 올 수도 있다.
그런데, 재귀라는 것은 말 그래도 스스로의 함수를 호출하는 방식을 의미하는 것이므로 DFS가 재귀를 이용해 탐색을 수행하는 것으로 하나의 방식이라 이해하면 된다.
또한 백트랙킹은 재귀를 통해 알고리즘을 풀어 가는기법 중 하나로 가지치기를 통해 탐색을 시도하다가 유망하지 않으면 추가 탐색을 하지 않고 다른 해를 찾는 방법이다.
DFS는 기본적으로 모든 노드를 탐색하는 것이 목적이지만 상황에 따라서 백트랙킹 기법을 혼용하여 불필요한 탐색을 그만두는 것이 가능하다!