- 코드잇 강의 바로 가기

에다 부스트

01. Boosting

Review)
Bagging : Bootstrap aggregating의 줄임말로, 임의로 bootstrap 데이터 셋을 만들고 이를 통해 만든 수많은 모델들의 결정을 종합하는 방식이다.

• Boosting
  성능이 별로인 모델들(weak learner)을 앙상블로 합쳐 성능을 극대화하는 방식이다. boosting도 앙상블 기법이기 때문에 여러 개의 모델들을 합치는 것은 Bagging과 동일하다.

  하지만 Bootstrapping처럼 데이터 셋을 임의로 만들지 않고, 먼저 만든 모델들이 어떻게 예측을 했는지에 따라서 뒤에 만드는 모델들의 데이터 셋들을 정한다는 차이점이 있다. 또 마지막으로 결정을 내릴 때 단순다수결을 쓰지 않고, 성능이 더 좋은 모델들의 예측값을 더 많이 반영하는 방식을 사용한다.
  
  
  

02. 에다 부스트

1. 성능이 별로 좋지 않은 결정 스텀프들을 많이 만든다.
2. 스텀프를 만들 때, 전 스텀프들에서 예측이 틀린 데이터들의 중요도를 더 높게 설정해준다.
3. 최종 결정을 내릴 때, 성능이 좋은 결정 스텀프의 예측 의견은 높은 비중으로, 그렇지 않은 스텀프에는 낮은 비중으로 반영한다.

• 스텀프(stump)하나의 질문과 그 질문에 대한 답을 바로 예측하는 결정 트리를 "스텀프"라고 한다. 스텀프는 주로 50%보다 조금 나은 성능을 갖는데, Boosting 기법은 일부러 성능이 안좋은 모델들(weak learner)을 사용하기 때문에 깊은 결정 트리 대신 스텀프만을 사용한다.
  
  

• 데이터 셋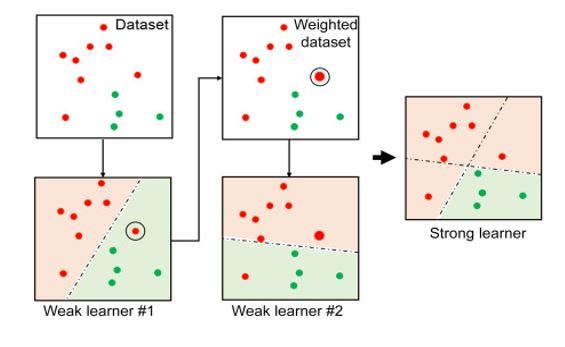이전 스텀프에서 분류한 결과를 바탕으로 틀리게 예측한 데이터의 중요도는 올리고, 맞게 예측한 데이터의 중요도는 낮춰 다음 데이터 셋을 만들어준다.

  뒤에 만든 스텀프에서 중요도가 높은 데이터들을 더 우선적으로 맞추기 때문에, 예측이 맞는지 여부에 따라 데이터들의 중요도를 조절해 다음 스텀프에서는 틀린 데이터를 좀 더 잘 예측할 수 있도록 만든다.
  이 과정을 반복하면서 각 스텀프는 전에 있던 스텀프들의 실수를 바로잡는 방향으로 만들어지게 된다.
  
  

• 예측
  에다 부스트는 성능 주의적으로 예측을 한다.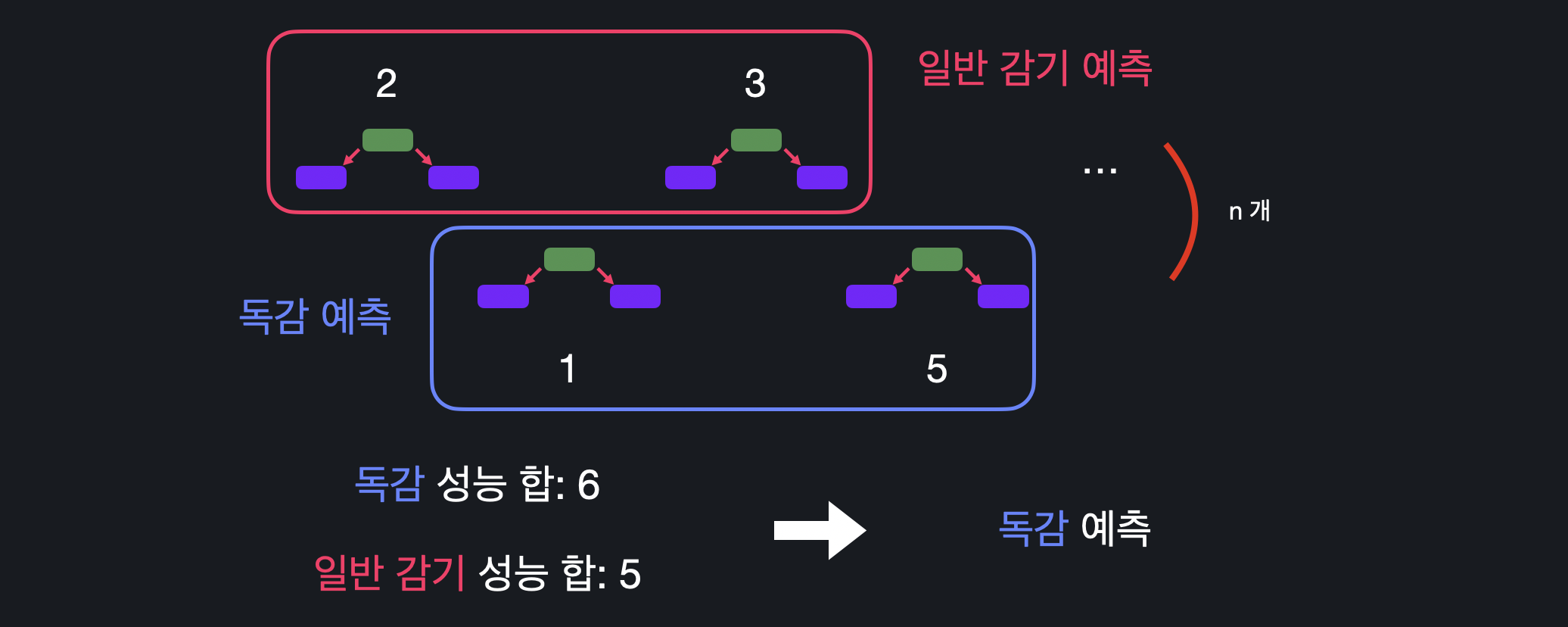위 예시처럼 다수결 상으로는 2:2여도 성능의 합이 더 높은 결정을 따른다.
  
  
  

03. 스텀프 성능 계산하기

다음과 같은 데이터 셋이 있을 때, 실제 속성으로 추가하는 것은 아니지만 '중요도'라는 열을 새롭게 나타내준다.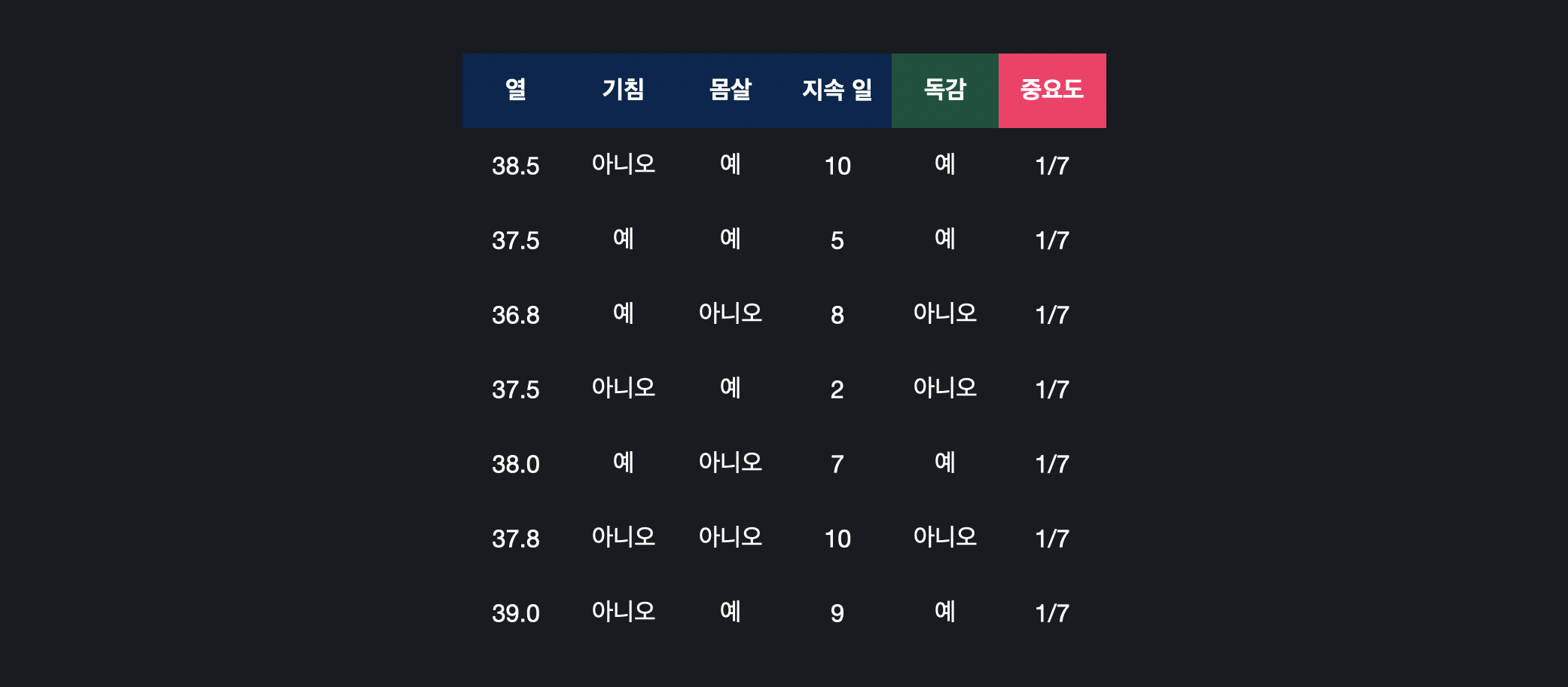처음에는 틀리게 예측한 데이터가 없으므로 모든 데이터의 중요도를 같게 초기화해주고 항상 중요도의 합은 1로 유지해줘야 한다.

1. 첫 스텀프 만들기
   결정 트리를 만들 때와 똑같이, 각 질문들의 지니 불순도를 계산하고 가장 불순도가 낮은 질문을 기준으로 스텀프를 만든다.

2. 스텀프 성능 계산하기
   에다 부스트는 이전 스텀프의 성능을 반영하기 때문에 미리 스텀프마다 성능을 계산해줘야 한다. 특정 스텀프의 성능은 다음 공식으로 구할 수 있다.

   $\frac{1}{2}log(\frac{1 - total\,error}{total\,error})$
   • total error : 잘못 분류한 데이터들의 중요도의 합

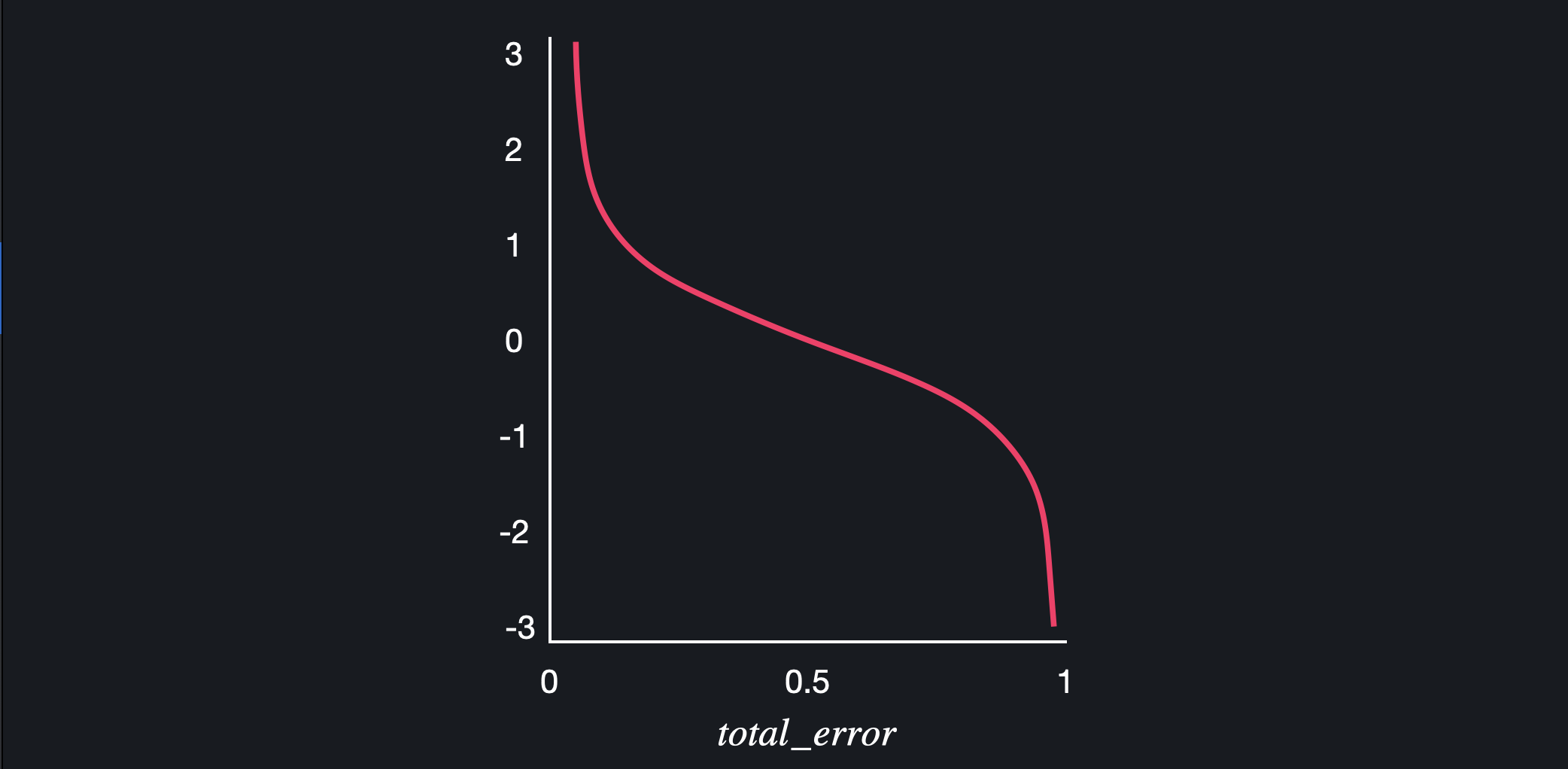성능식을 그래프로 나타내면, total error가 1에 가까워질수록 성능이 작아지고 0에 가까워질수록 성능이 커지는 것을 볼 수 있다.

데이터 중요도의 총합은 항상 1이기 때문에 total error가 1이라는 것은 스텀프가 모든 데이터를 다 틀리게 예측한 경우를 뜻한다. 성능이 엄청 안좋다는 의미이기 때문에 성능을 무한히 작게 만들어주는 것이다.
반대로 total error가 0이라는 말은, 스텀프가 모든 데이터를 다 맞게 예측한 경우로스텀프의 성능이 매우 좋은 것이기 때문에 성능을 무한히 크게 만들어준다.
total error가 0.5면, 예측이 반은 맞고 반은 틀린 것으로 성능이 아무 의미가 없기 때문에 0으로 만들어주게 된다.

정리하자면, 스텀프가 예측을 잘할수록 또는 잘 못할수록 성능을 기하급수적으로 늘리고 줄여주는 것이다.

04. 데이터 중요도 바꾸기

<03. 스텀프 성능 계산하기>에서는 스텀프의 성능을 계산하는 방법에 대해 보았다. 이번에는 틀리게 예측한 데이터의 중요도는 높여주고, 맞게 예측한 데이터의 중요도는 줄여주는 방법에 대해 알아볼 것이다.

처음 스텀프를 만들 때는 틀리게 예측한 데이터가 없기 때문에 모든 데이터의 중요도가 동일했는데, 다음 스텀프를 만들 때는 각 데이터가 맞게 분류되었는지 아닌지에 따라 중요도를 바꿔줘야 한다.

먼저 틀리게 분류한 모든 데이터는 다음 공식으로 중요도를 바꿔준다.

제대로 분류한 데이터는 다음과 같이 중요도를 바꿔준다.

• $weight_{new}$ : 예전 중요도
• $weight_{new}$ : 새로운 중요도
• $p_{tree}$ : 스탬프의 성능
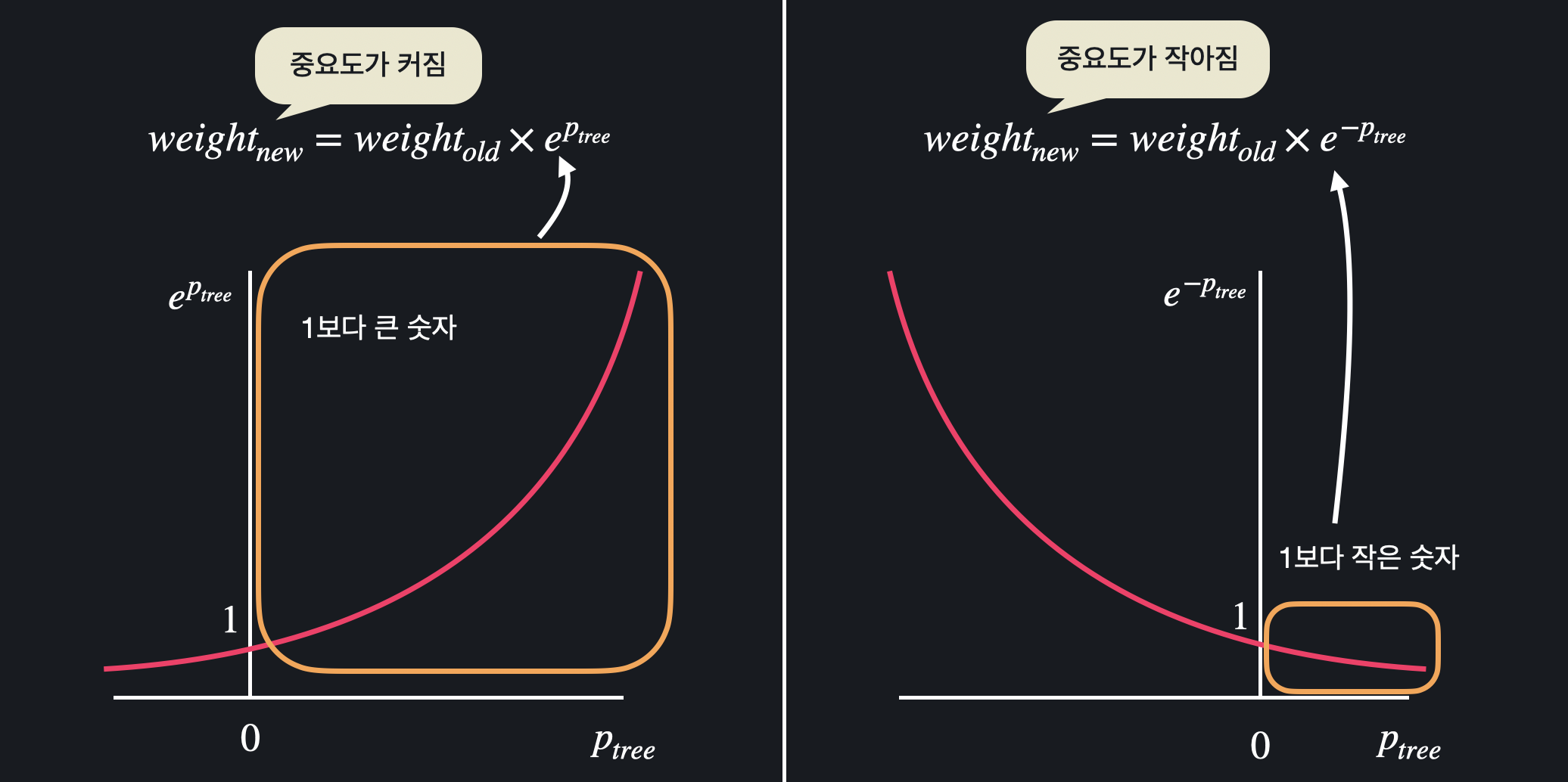  그래프로 보면, 스텀프의 성능이 커질수록 틀리게 예측한 데이터의 중요도가 커지고, 반대로 맞게 예측한 데이터의 중요도는 작아지는 것을 볼 수 있다.
  스텀프가 데이터를 반 이상만 맞추면 틀린 데이터는 원래 중요도에 1보다 큰 값을 곱하니까 원래 중요도보다 커지게 되고, 맞은 데이터는 원래 중요도에 1보다 작은 값을 곱하니까 더 작아지는 것이다.
  둘 다 스텀프의 성능이 0일 때는 중요도가 1이 나오게 된다.
  
  
  

05. 스텀프 추가하기

<04. 데이터 중요도 바꾸기>를 통해 중요도가 바뀐 데이터 셋을 이용해서 새로운 스텀프들을 만드는 방법을 알아볼 것이다.

각 데이터의 중요도를 새 데이터 셋에 들어갈 확률로 취급해서 새로운 데이터 셋을 만들어 준다. 그러기 위해서는 먼저 각 데이터의 중요도를 이용해 범위를 정해줘야 한다.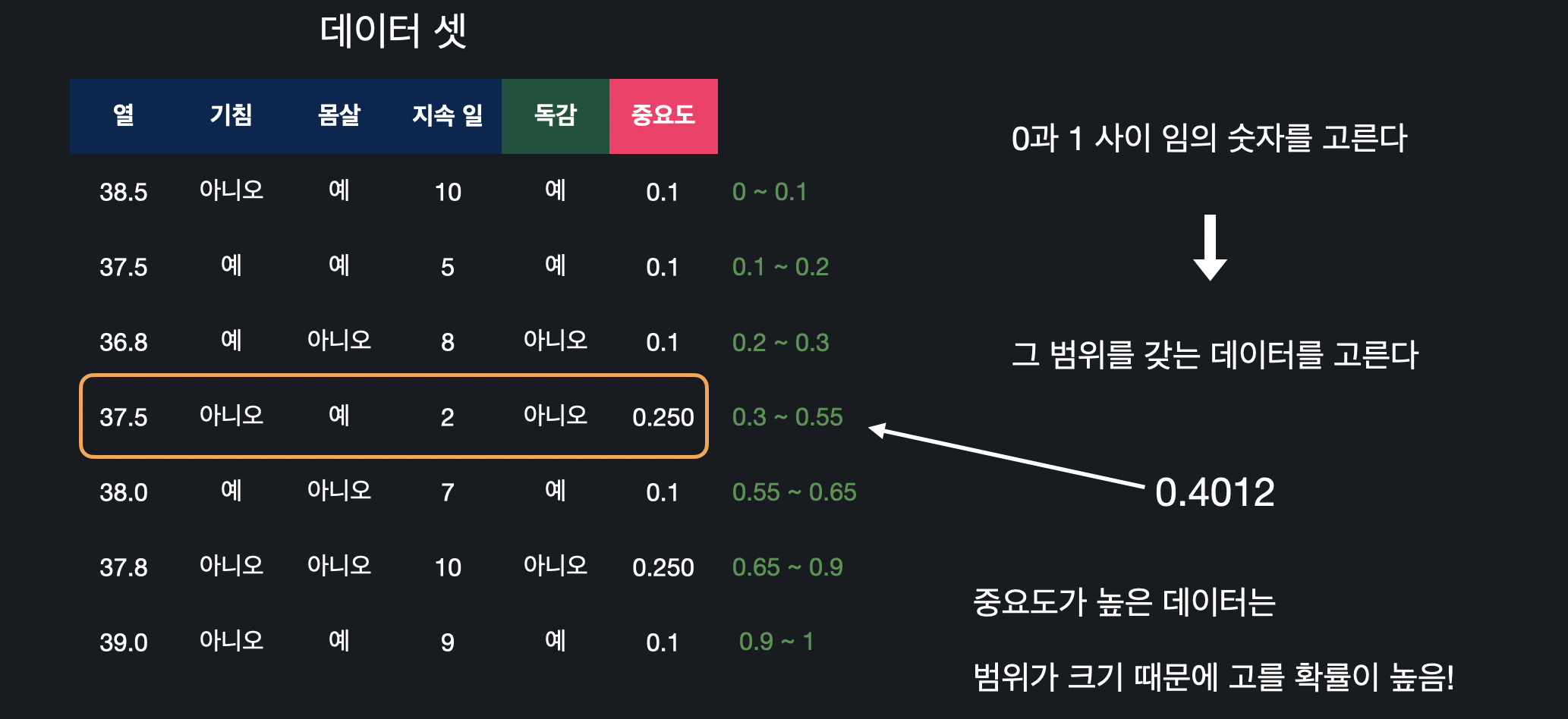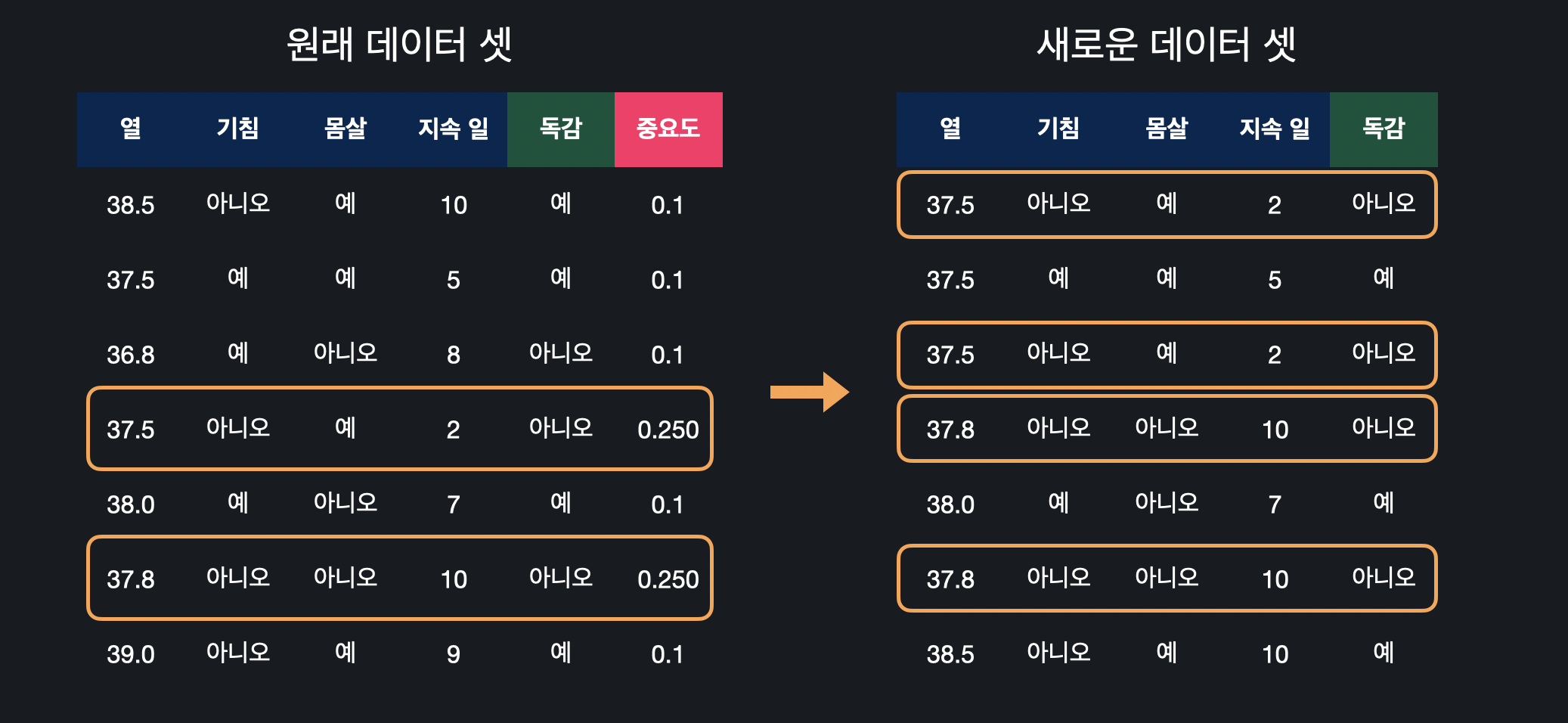중요도를 통해 데이터의 범위를 구한 후, 0 ~ 1 중 임의로 고른 수가 포함되는 데이터를 새로운 데이터 셋에 추가해준다. 이 과정을 원래 데이터 셋의 크기만큼 반복하면 새로운 데이터 셋을 만들 수 있다.

데이터의 중요도가 높을수록 새로운 데이터 셋에 들어갈 확률이 높고, 중요도가 낮으면 아예 새로운 데이터에 추가되지 않을 수도 있다. 이렇게 중요도를 이용해, 전 스텀프에서 틀린 데이터가 새로운 데이터 셋에 더 많이 들어가게 되면서 예측이 틀린 데이터를 더 잘 맞출 수 있게 된다.

이렇게 만든 새 데이터 셋을 이용해 다시 지니 불순도를 계산해 스텀프를 새로 만들 수 있고, 이 과정을 반복해주면 된다.

06. 예측하기

에다 부스트는 최종 예측을 할 때 더 성능이 좋은 스텀프들의 예측 의견에 더 큰 비중을 둔다.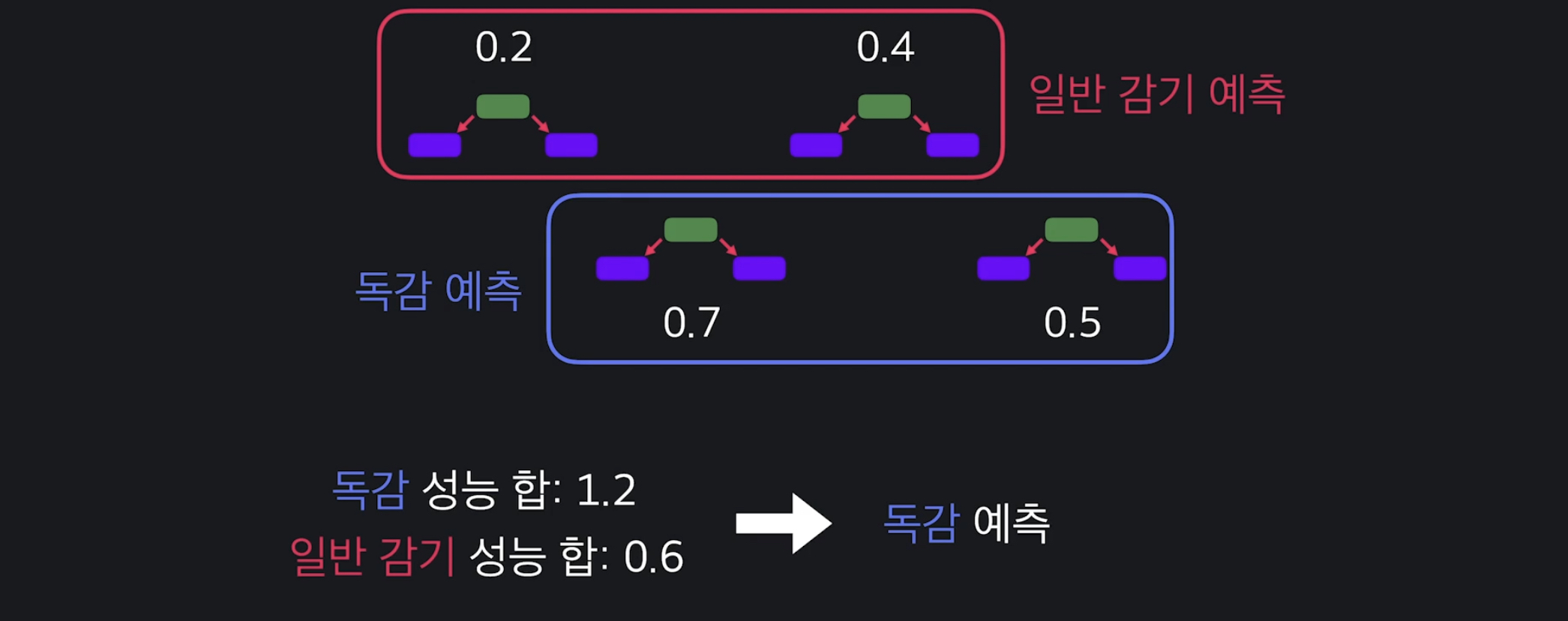위의 예시처럼 독감 예측 스텀프와 일반 감기 예측 스텀프가 각각 2개씩 동일하게 있어도 독감 예측 스텀프의 성능이 더 높기 때문에 최종적으로 독감으로 결정하는 것이다.

수많은 스텀프가 있더라도 똑같이, 특정 분류를 하는 스텀프들의 성능을 모두 더해서 성능이 좋은 스텀프를 더 많이 반영해서 결정을 내리면 된다.