- 코드잇 강의 바로 가기

선형 회귀

01. 선형 회귀 (Linear Regression)

선형 회귀 : 데이터들을 놓고 그것을 가장 잘 설명할 수 있는 선을 찾는 분석 방법
이 때 이 선을 최적선(line of best fit) 이라 부른다.
선형 회귀에서 최적선은 직선 y = ax+b 형태로 표현되는데 결국 선형 회귀의 임무는 계수 a와 상수 b를 찾아내는 것이다.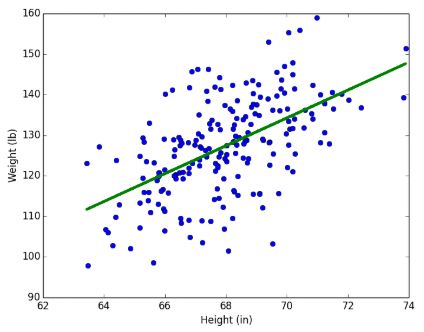예를 들어 키와 몸무게 데이터를 놓고 그에 대한 최적선을 구하면, 특정 사람의 키를 바탕으로 몸무게를 예측할 수 있다.

• 목표 변수(target value, output value) : 맞추려고 하는 값
• 입력 변수(input value, feature) : 목표 변수를 맞추기 위해 사용하는 값
  키-몸무게 예측 상황에서 키는 입력 변수이고, 몸무게는 목표 변수가 된다.
• 데이터 표현법
  • $m$ : 학습 데이터의 개수
  • $x$ : 입력 변수
  • $y$ : 목표 변수
  • $i$번째 데이터는 $x^{(i)}$, $y^{(i)}$처럼 각 데이터들은 번호를 써서 표현한다.

02. 가설 함수 (Hypothesis function)

가설 함수 : 최적선을 찾아내기 위해 시도하는 다양한 함수들

• 가설 함수 표현법
  목표 변수에 영향을 미치는 입력 변수가 여러 개일 때, 일관성 있게 하기 위해 다음과 같이 표기한다.
  $θ_0$은 상수항으로 곱해지는 입력 변수가 없지만 통일성을 위해 항상 $x_0 = 1$로 고정하고 아래와 같이 표기하기도 한다.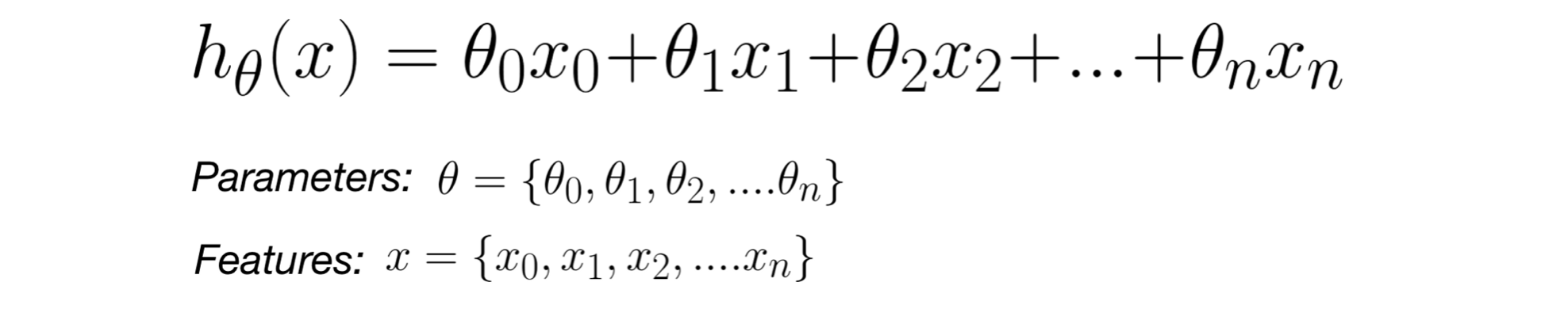 선형 회귀의 임무는 가장 적절한 세타 값들을 찾아내는 것이다.

03. 평균 제곱 오차 (Mean Squared Error; MSE)

평균 제곱 오차 : 데이터들과 가설 함수가 평균적으로 얼마나 떨어져 있는지 나타내기 위한 하나의 방식으로, 가설 함수가 얼마나 좋은지 평가하는 방법 중 선형 회귀에서 가장 많이 쓰는 방법이다. 모든 데이터에 대해 각 입력 변수에 대한 실제 결과와 예측값 사이의 오차를 구한 후 제곱하고, 모두 더해 총 데이터의 개수만큼 나눠 평균을 구하면 된다.
평균 제곱 오차가 크다는 것은 가설 함수와 데이터들 간의 오차가 크다는 것을 뜻하기 때문에 평균 제곱 오차가 클수록 그 가설 함수가 데이터들을 잘 표현하지 못함을 의미한다.

• 오차를 제곱해서 더하는 이유
  1. 오차가 음수이든 양수이든 똑같이 취급하기 위해서
  2. 오차가 커질수록 더 부각시키기 위해서
     (더 큰 오차에 대해 더 큰 패널티를 주기 위해)
     
     
• 오차의 절댓값을 사용하지 않는 이유
  1. 절댓값 그래프에는 뾰족한 첨점이 있고, 이는 미분이 불가능한 조건이다.
  2. 최적선을 구한 경우, 잔차를 모두 더하면 합이 0이 된다. 만들어진 여러 최적선 중 잔차가 최소인 최적선을 찾기 위해 절댓값 대신 제곱을 사용한다.

04. 손실 함수 (Loss Function)

손실 함수($J$) : 어떤 가설 함수를 평가하기 위한 함수
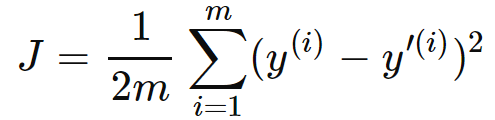손실 함수의 아웃풋이 작을수록 가설 함수의 손실이 적기 때문에 더 좋은 가설 함수라고 할 수 있다.

• 손실 함수의 input : 세타 $θ$
  선형 회귀에서는 가설 함수의 세타값들을 잘 조율해 가장 적합한 가설 함수를 찾아내야 한다.
  따라서 손실 함수의 아웃풋은 이 세타 값들을 어떻게 설정하느냐에 따라 결정된다. 일반적으로 $x, y$를 변수라 생각할 수 있지만 오히려 $x$와 $y$에 정해진 데이터를 대입하는 것이기 때문에 상수로 취급해줘야 한다.

05. 경사 하강법 (Gradient Descent)

경사 하강법 : 손실 함수의 아웃풋을 최소화하기 위한 방법으로, $θ$를 계속 업데이트해 최적화시킨다.
파라미터를 임의로 정한 다음 편미분을 통해 조금씩 변화시켜가며 손실을 점점 줄여나가 결국 최적의 파라미터($θ$)를 찾는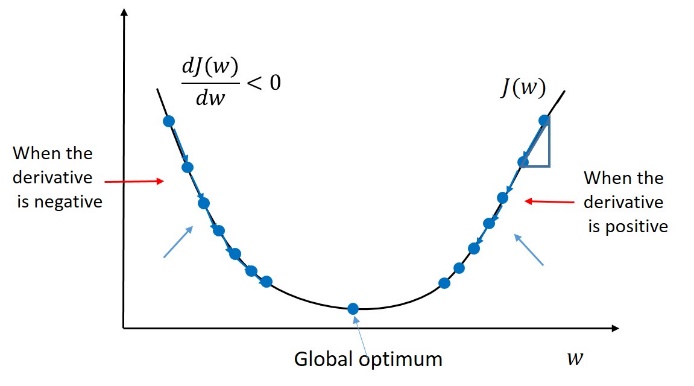다.

• 경사 하강법의 계산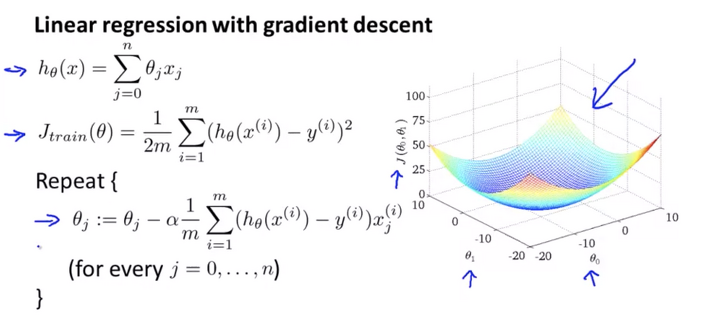모든 인풋 θ에 대해 손실 함수 식을 편미분해주고 그 결과를 각 $θ$에 업데이트하는 기존 공식에 대입해준다.
  => 위 공식을 이용해 $θ$를 반복적으로 업데이트하면, 결국에는 손실을 최소화하는 최적선을 구할 수 있다.
  

06. 학습률 α

학습률 : 경사 하강법에서 경사를 내려갈 때마다 얼마나 많이 그 방향으로 갈 것인지를 결정하는 변수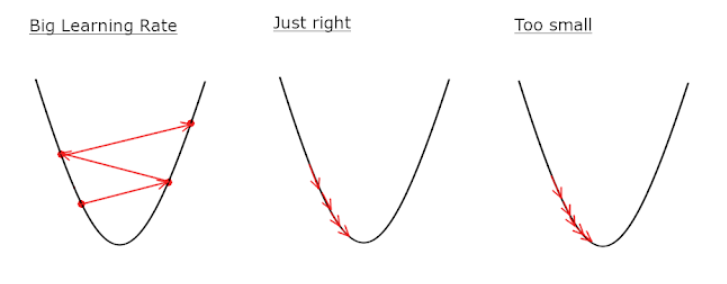
1. 학습률이 너무 큰 경우
경사 하강을 한 번 할 때마다 θ값이 많이 바뀌게 된다. 이때 α가 너무 크면 경사 하강법을 진행할 수록 손실 함수 $J$의 최소점에서 멀어질 수 있고 손실 그래프가 커지게 된다.
2. 학습률이 너무 작은 경우
경사 하강을 한 번 할 때마다 $θ$가 너무 조금씩 이동하게 된다. $α$가 너무 작으면 빠른 시간 안에 끝낼 수 있는 작업이 훨씬 많은 시간을 잡아먹게 되고 iteration 수가 너무 많아진다.
3. 적절한 학습률
빠르고 정확하게 손실 함수 $J$의 최소점까지 도달하는 학습률이 가장 좋다고 할 수 있다. 적절한 학습률은 상황과 문제에 따라 달라진다. 일반적으로 1.0 ~ 0.0 사이의 숫자로 정하고 여러 개를 실험해보면서 경사 하강을 제일 적게 하면서 손실이 잘 줄어드는 학습률을 선택한다.

07. 모델 평가하기

모델 : 세상에 일어나는 상황을 수학적으로 표현한다는 의미에서, 최적선을 가지는 가설 함수를 나타낸다.
머신 러닝에서 데이터를 이용해 모델을 개선시키는 것을 '모델을 학습시킨다'라고 한다.

모델이 잘 학습되었는지 평가하기 위해서 '평균 제곱근 오차'를 이용한다.

• 평균 제곱근 오차(Root Mean Square Error; RMSE) : 앞서 배운 평균 제곱 오차(MSE)에 루트를 씌운 값
  데이터에 맞게끔 모델을 학습시키면 당연히 평균 제곱근 오차가 낮게 나오는 문제가 발생한다.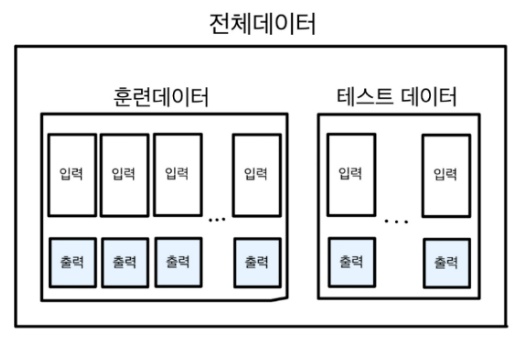
  따라서 신빙성 있게 모델을 평가하기 위해 데이터를 '학습 데이터(training set)'과 '평가 데이터(test set)'으로 분리한다.