- 코드잇 강의 바로 가기

다중 선형 회귀

01. 다중 선형 회귀(Multiple Linear Regression)

• 다중 선형 회귀 : 여러 개의 입력 변수를 사용해서 목표 변수를 예측하는 선형 회귀 알고리즘
  지난 포스팅에서의 선형 회귀는 하나의 입력 변수만 갖고 목표 변수를 예측했지만 머신 러닝을 할 때 입력 변수가 하나밖에 없는 경우는 굉장히 드물다.
• 다중 선형 회귀 문제 표현
  • 입력 변수를 'featute(속성)'라고 하며, $x$로 나타낸다.
    첫 번째 입력 변수(첫 번째 행)는 $x_1$, 두 번째 입력 변수는 $x_2$, 세 번째 입력 변수는 $x_3$와 같이 표현한다.
    입력 변수의 개수는 $n$이라는 문자로 표현하고 위의 예시에서는 $n$ = 3이 된다.
  • 목표 변수는 이전과 동일하게 한 개로, $y$로 나타낸다.
  • 학습 데이터의 개수는 $m$으로 표현한다.
    만약 50개의 데이터를 갖고 프로그램을 학습시킨다면, $m$= 50이다. 첫 번째 데이터의 입력 변수(첫 번째 열 전체)는 $x^{(1)}$로, 목표 변수는 $y^{(1)}$로 표현한다. 이때 $x^{(1)}$는 그냥 하나의 값이 아니라, 여러 값을 담은 하나의 벡터이다.
    따라서 $x^{(1)}$에는 첫 번째 데이터의 각 속성마다의 값이 모두 저장되어 있다. 각 데이터에서 특정 속성의 값을 알고 싶을 때는 아래와 같이 표현한다.
    예를 들어 3번째 데이터의 2번째 속성 값을 나타내고 싶다면(3번째 열, 2번째 행), $x_2^{(3)}$처럼 쓰면 된다.
    이를 일반화하여 i번째 데이터의 j번째 속성은 $x_j^{(i)}$으로 나타낼 수 있다.
    
    

02. 다중 선형 회귀 가설 함수

다중 선형 회귀에서 가설 함수는 $h_θ(x) = θ_0 + θ_1x_1 + θ_2x_2 + ... + θ_nx_n$ 와 같이 쓰고, 항이 많아졌을 뿐 여전히 일차 함수이다.
$x_1, x_2, x_3, ..., x_n$처럼 여러 개의 입력 변수가 있다.

집 데이터로 예를 들면,
$x_1$는 집 크기, $x_2$는 방 수, $x_3$는 지하철까지의 거리이고
$θ_1$은 집 크기가 집 가격에 미치는 영향, $θ_2$는 방 수가 가격에 미치는 영향, $θ_3$는 지하철까지의 거리가 가격에 미치는 영향으로 생각하면 된다.

이렇게 모든 항들을 다 더해 결과적으로 집 가격을 예측할 수 있게 된다.
다중 선형 회귀도 선형 회귀와 마찬가지로, θ값들을 조율하면서 학습 데이터에 가장 잘 맞는 θ값들을 찾아내는 것이 목적이다.

• 행렬 표현
  가설 함수의 형태가 길고 복잡하기 때문에 이를 선형대수학의 벡터를 사용해 간결하게 표현할 수 있다.
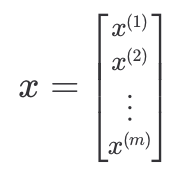  선형 회귀처럼 속성이 하나일 때의 모든 데이터는 열벡터로 나타낼 수 있고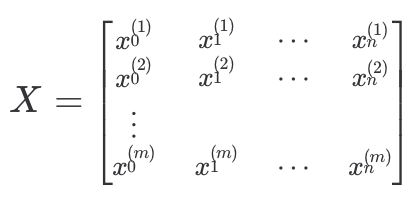다중 선형 회귀처럼 속성이 여러 개라면 행렬을 통해 표현할 수 있다.
  이렇게 입력 변수 데이터를 행렬로 묶어 표현한 것을 설계행렬(Design Matrix)라 한다.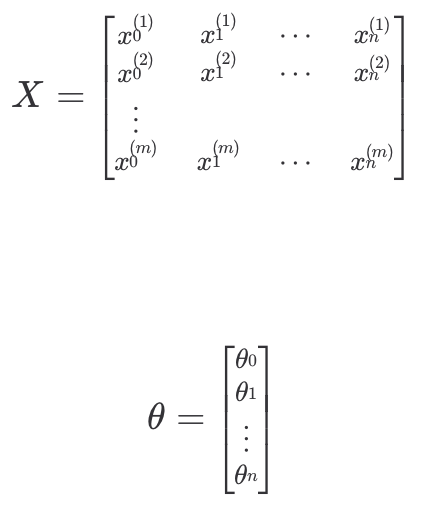 입력 변수와 파라미터를 위와 같이 행렬과 벡터로 표현하면 (이때 $x_0$은 항상 1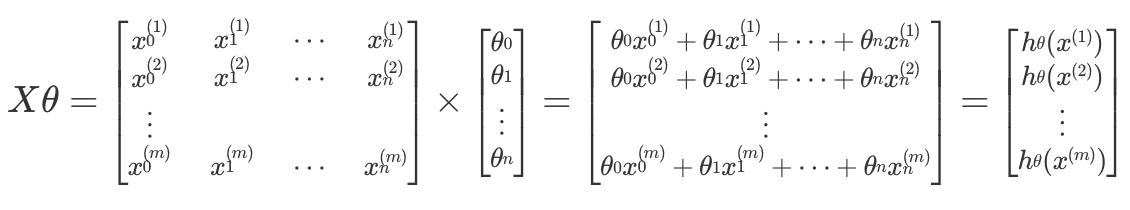이다.)가설 함수는 두 행렬의 곱으로 표현할 수 있어 각 열에 각 데이터에 대한 예측값이 계산될 것을 확인할 수 있다.
  따라서 가설 함수는 $h_θ(x) = θ^Tx$ 와 같이 표현할 수 있다.
  
  

03. 손실 함수 $J(θ)$를 최소화하는 $θ$ 찾기

Review)
최적선 : 데이터가 있다고 가정할 때, 이 데이터에 가장 잘 맞는 선
가설 함수 : 최적선을 찾기 위해 시도해 보는 모든 선
손실 함수 : 가설 함수를 평가하는 기준으로, 손실 함수의 결과값이 작을수록 좋은 가설 함수이다. 이때 손실 함수는 어떤 θ값을 쓰냐에 따라 결과가 달라지기 때문에 θ에 대한 함수이다.
경사 하강법 : 손실 함수의 결과값을 낮추기 위해, 가장 가파르게 내려가는 방향(손실을 가장 빠르개 줄알 수 있는 방향)으로 계속해서 θ값을 이동하는 것

1. 다중 선형 회귀 경사 하강법

다중 선형 회귀에서의 경사 하강법 역시 선형 회귀에서의 방식과 거의 동일하다. 다중 선형 회귀에서도 손실 함수는 선형 회귀와 똑같이 생겼다.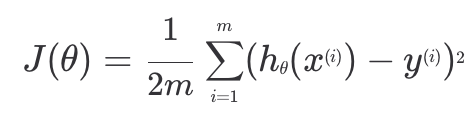다중 선형 회귀는 입력 변수가 여러 개이기 때문에 여러 개의 θ값을 업데이트하기만 하면 된다.
$n$개의 입력 변수가 있다고 하면, $θ_0$ ~ $θ_n$까지 쭉 업데이트해야 경사 하강을 한 번 했다고 할 수 있다. 경사 하강을 한 번 할 때마다, 손실을 최대한 빨리 감소시키는 방향으로 θ값들이 업데이트 되고, 이 과정을 충분히 반복하면 결국 손실을 최소에 가깝게 줄일 수 있다.
결과적으로 학습 데이터에 잘 맞는 θ값들을 찾아 데이터에 잘 맞는 가설 함수를 찾을 수 있게 된다.


위의 내용을 코드로 구현하기 쉽게 바꾸기 위한 방법은 아래와 같다.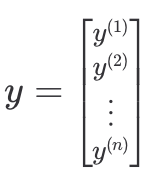목표 변수는 값이 하나이기 때문에 열벡터로 나타낼 수 있고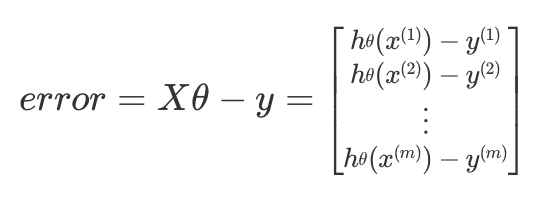위에서 구한 가설 함수 식을 이용해 모든 예측값들과 목표 변수의 차이를 위와 같이 표현할 수 있다.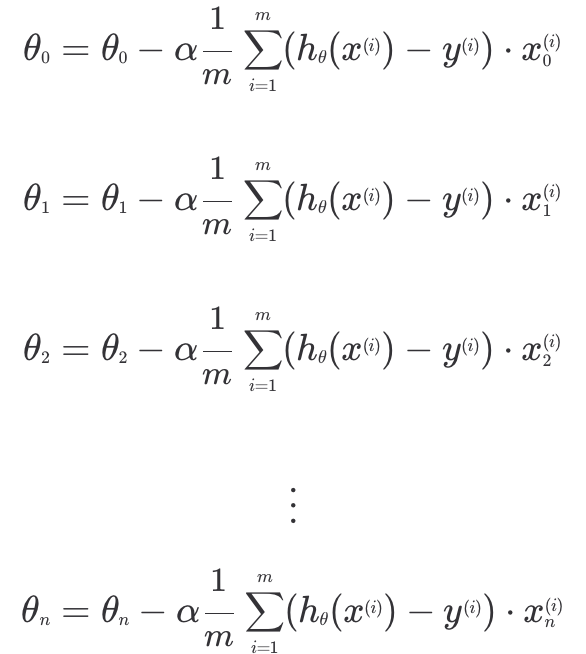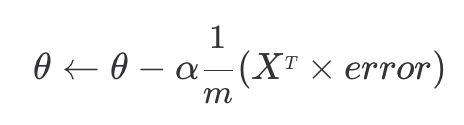이 과정을 거쳐 경사 하강법 공식을 간단한 행렬 연산으로 나타낼 수 있게 된다.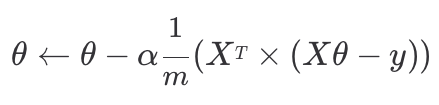결과적으로 이렇게 간단한 행렬식으로 경사 하강법 공식을 표현할 수 있게 된다.

2. 정규 방정식

다항 선형 회귀에서 θ를 구할 수 있는 또다른 방법으로는 정규 방정식이 있다.

• 정규 방정식 : 미분한 손실 함수의 결과값이 0이 되는 θ값 찾기
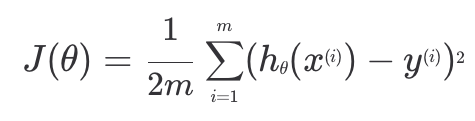  먼저 손실 함수를 행렬식으로 표현하려면 평균 제곱 오차를 구해야 한다.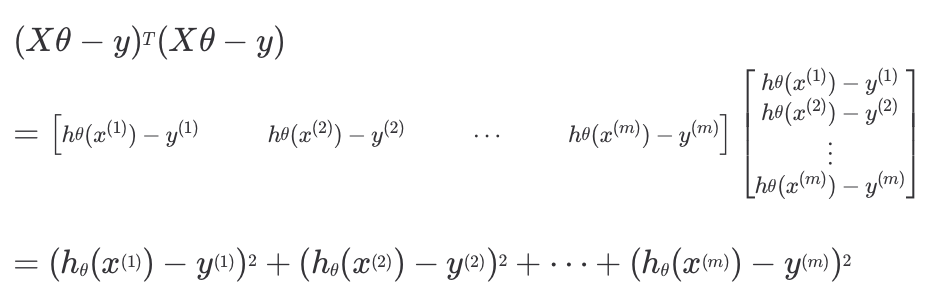( 학습 데이터에 대한 예측값 - 목표 변수 )2 를 위와 같이 계산할 수 있고
  결과적으로 손실 함수는 행렬 연산으로는 간단하게 아래와 같이 표현할 수 있다.
  

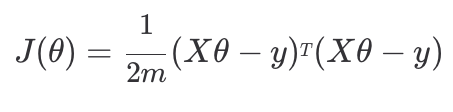
정규 방정식을 풀기 위해 손실 함수를 θ에 대해 미분하는 과정은 아래와 같다.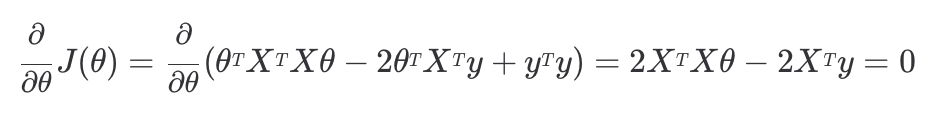1 . 행렬 연산으로 표현한 손실 함수 행렬 공식을 전개해준다. 미분 함수가 0이 되는 지점을 찾으려는 것이기 때문에 곱해져 있는 상수 1/2m은 무시해도 된다.
2. 첫 번째 항 $θ^TX^TXθ$는 θ가 맨 앞, 맨 뒤에 한 번씩 곱해져 있어 $θ^2$라고도 할 수 있기 때문에, 미분하면 $2X^TXθ4$가 된다.
3. 두 번째 항 $-2θ^TX^Ty$는 θ가 한 번 곱해져 있어, 미분하면 $2X^TXy$가 된다.
4. 세 번째 항 $y^Ty$는 θ가 없어 상수항 취급해주기 때문에, 미분하면 0이 된다.

따라서 정규 방정식은 $2X^TXθ - 2X^Ty = 0$을 만족하면 θ를 구해주면 되는 것이다. 이때 θ만 남기고 나머지를 이항하여 $θ = (X^TX)^{-1}X^Ty$ 식으로 최적의 θ를 구할 수 있다.

• 경사 하강법 VS. 정규 방정식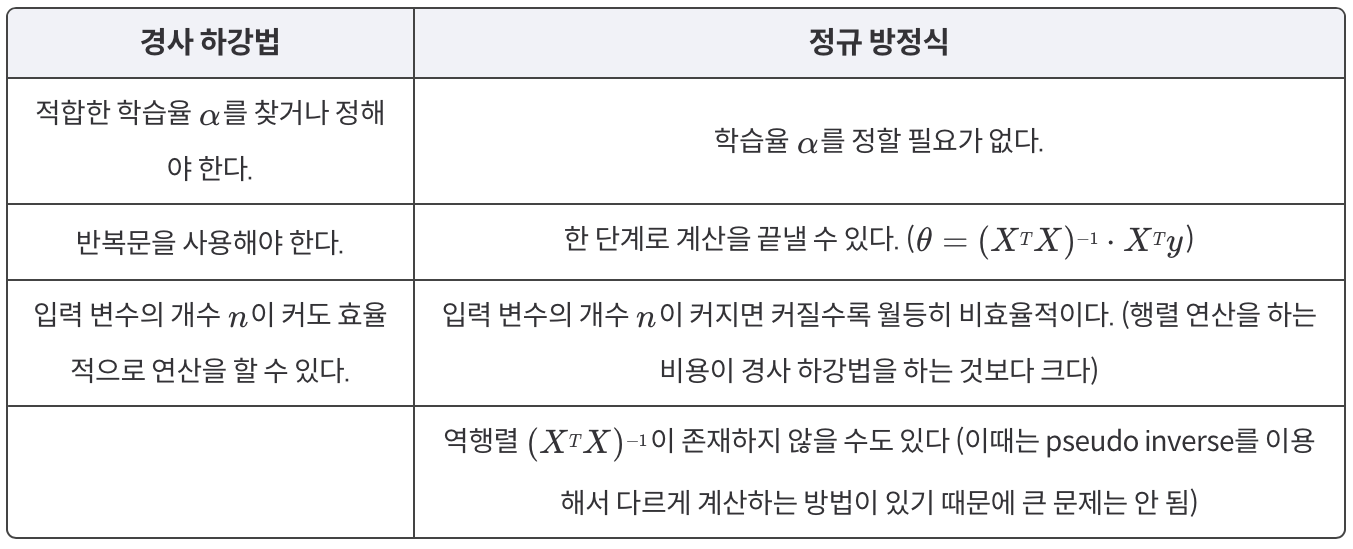입력 변수(속성)의 수가 엄청 많을 때(보통 1000개를 넘으면)는 경사 하강법을, 비교적 입력 변수의 수가 적을 때는 정규 방정식을 사용한다.
  
  

4. Convex 함수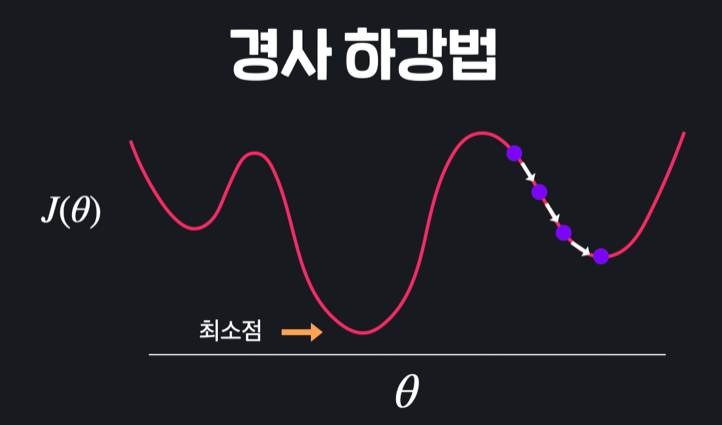

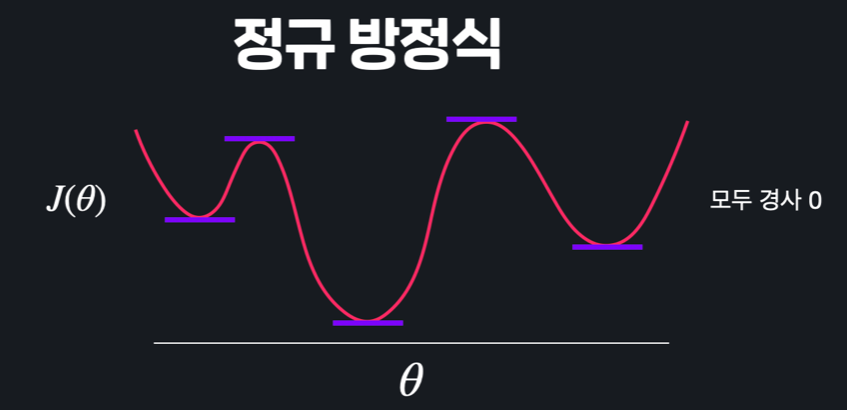
위와 같이 수많은 극솟값들과 극댓값들이 있으면 경사하강법이나 정규 방정식을 통해 구한 극소 지점이 손실 함수 전체에서 최소 지점이라 확실하게 얘기할 수 없어 손실 함수의 최저점을 찾아갈 수 없을 때도 있다.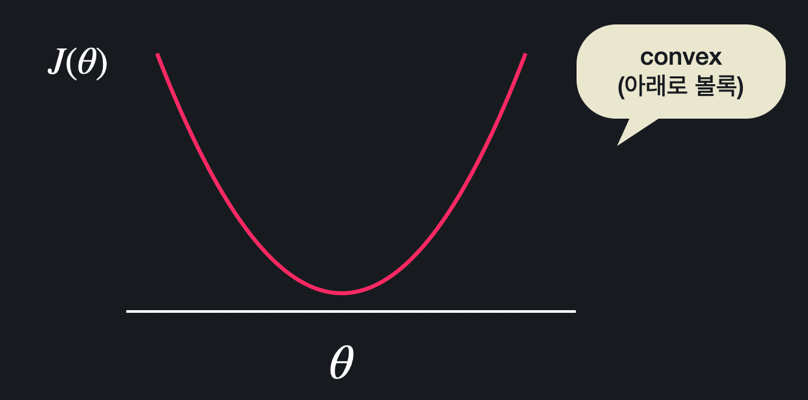반면 위와 같은 형태에서는 경사 하강법이든 정규 방정식이든 항상 손실 함수를 최소화하는 θ를 찾을 수 있다. 이러한 형태의 함수를 convex 함수(아래로 볼록한 함수)라고 한다.

선형 회귀에서 손실 함수로 사용했던 평균 제곱 오차(MSE)는 항상 convex함수이기 때문에 선형 회귀를 할 때는 항상 최적의 θ 값들을 구할 수 있다.