Module 4. 『딥러닝(Deep Learning)』 2. Training Neural Networks

📍 강의 자료 출처 : LG Aimers

2. 심층신경망(deep neural networks)의 학습 과정

기본적으로 gradient descent 알고리즘을 활용하여 신경망을 학습한다.

neural network의 학습 과정

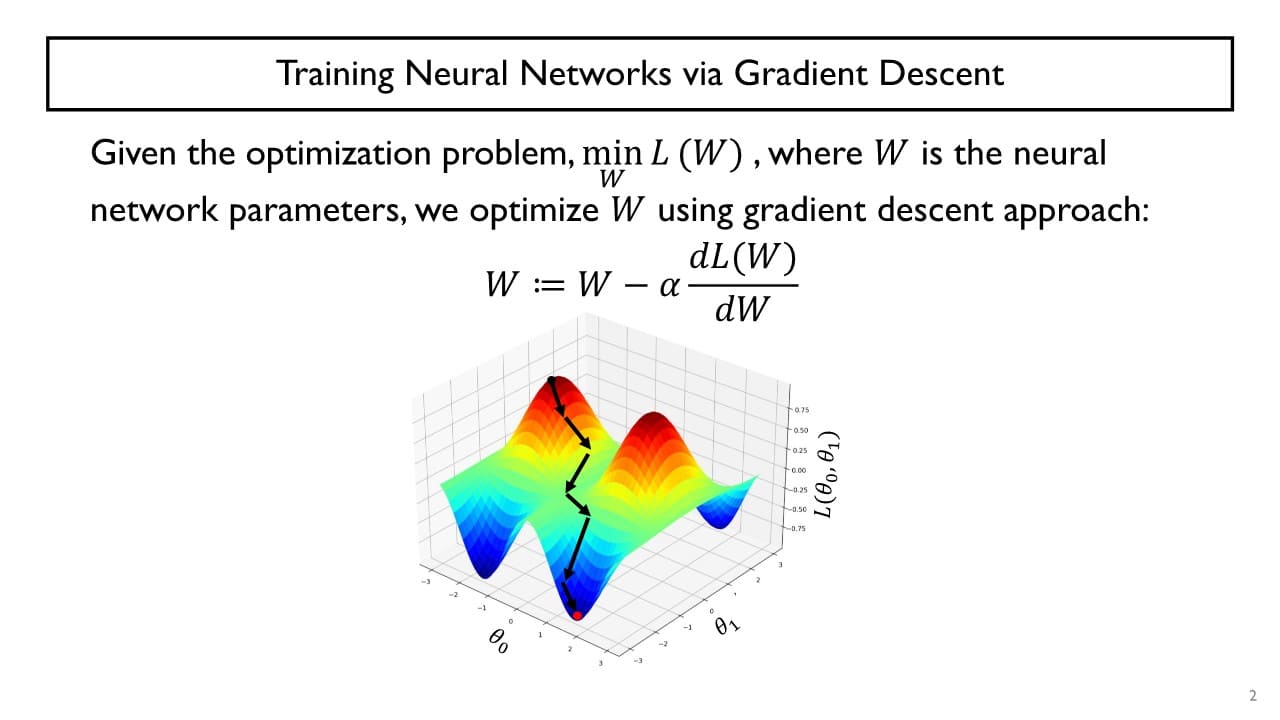$W$ : 최적화하고자 하는 neural network의 parameter들
출력을 미분하여 기울기를 구한 후 그 값의 반대 방향으로 step size만큼 곱해 기존 parameter $W$를 업데이트한다.

forward propagation (초록)
: 입력 데이터를 넣어 예측값을 구하는 과정
예측값과 정답의 차이가 최소가 되는 방향으로 loss function을 설정한다.
함수의 입력 : $W$ → 함수의 출력 : loss 값

backward propagation (빨강)
: loss function의 편미분(= 기울기)을 구하기 위해 parameter $W$를 업데이트하는 과정

Gradient descent를 사용하면 (특히 loss function이 복잡한 형태를 띄고 있을 때) 수렴 속도가 상대적으로 굉장히 느린 문제점이 발생한다.
cf> gradient descent의 여러 변형 중 Adam이 최근 좋은 성능을 보여 많이 사용되고 있다.

Sigmoid Activation

: 하나의 뉴런 혹은 perceptron이 입력 신호와 가중치의 선형결합에 Sigmoid function을 적용하여 0 ~ 1 사이의 실수 값으로 근사화하는 과정
⇒ 주어진 선형결합의 결과가 $[-∞, ∞]$ → $[0, 1]$로 mapping 된다.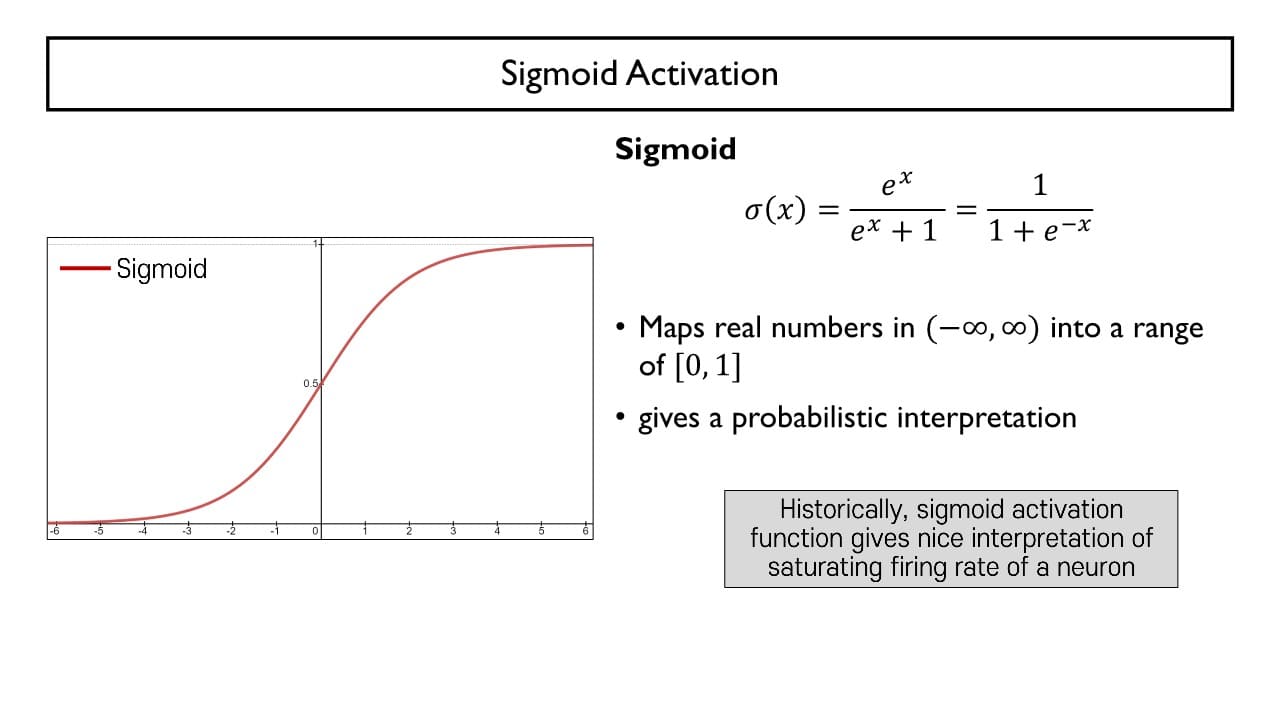

Gradient vanishing
Multi-layer인 경우 sigmoid function의 backpropagation을 수행할 때마다 gradient 값이 점점 작아져 앞쪽에 있는 parameter들은 제대로 업데이트되지 않는 문제가 발생할 수 있다.
→ 결과적으로 neural network 전체적으로 학습이 굉장히 느려지는 문제를 초래한다.

이러한 gradient vanishing 문제를 해결하기 위해 여러 activation function들이 등장했다.

1. Tanh Activation

: $2*sigmoid(x) - 1$
활성화 함수 출력값의 범위가 $[-1, 1]$로, sigmoid보다 넓어진다.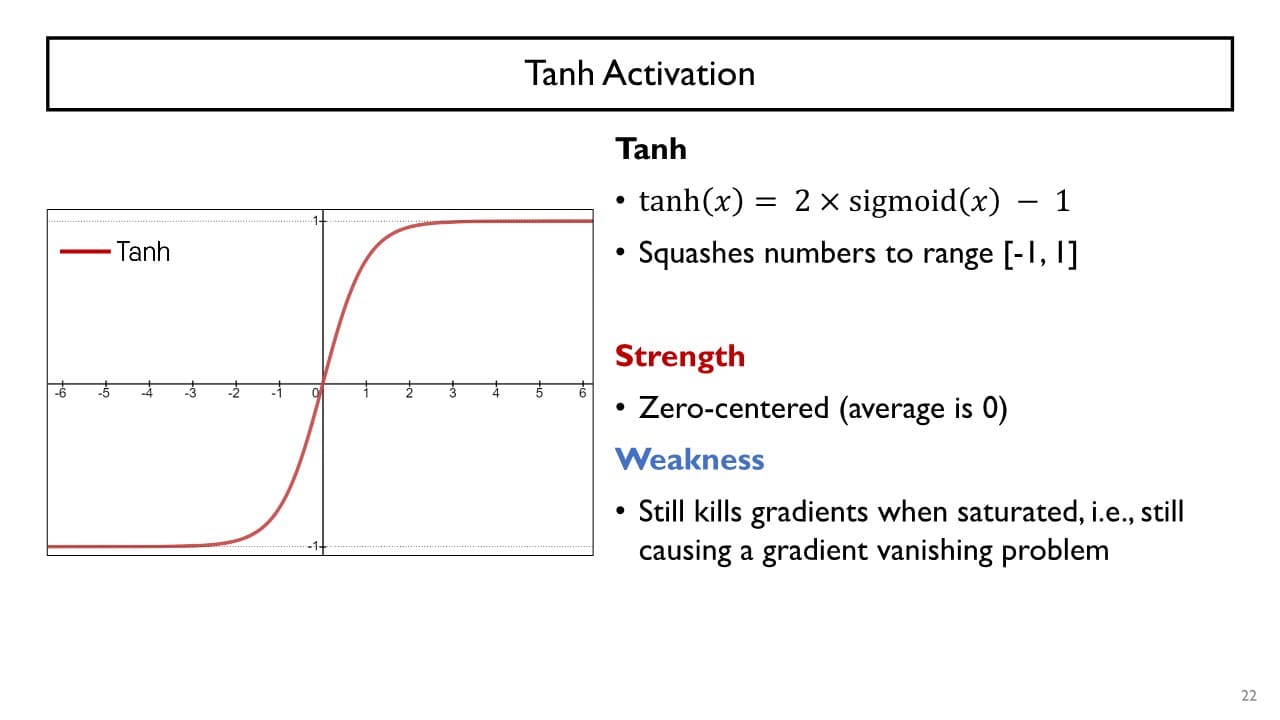

• 장점
  • 평균이 0을 중심으로 형성된다
    → 학습을 조금 더 빠르게 해주는 효과
• 단점
  • gradient의 범위가 $[0, \frac{1}{2}]$이기 때문에 gradient vanishing 문제를 여전히 가진다

2. ReLU (= Rectified Linear Unit)

: $max(0, x)$
활성화 함수 출력값의 범위가 $[0, x]$로, sigmoid나 tanh에서의 gradient vanishing 문제를 근본적으로 탈피할 수 있다.

• 장점
  • 계산이 빠르다
  • $x > 0$이면 gradient vanishing 문제가 발생하지 않는다
• 단점
  • 함수의 입력값$(x)$가 음수일 때 접선의 기울기가 완전히 0으로, output node에 어떤 값이 주어지든 이후 모든 gradient값이 0이 된다
  
  

Batch Normalization

: 활성화 함수를 사용할 때 추가적으로 학습을 용이하게 하는 뉴런 혹은 layer
gradient vanishing 문제를 해결하기 위해 입력값의 범위를 제한하는 방법이다.→ forward propagation 시 입력으로 주어지는 값들의 대략적인 범위를 ReLU일 때는 0 근처(tanh(sigmoid)일 때는 기울기가 0이 아닌 구간)로 제한한다.

예) batch size = 10이라면 10개의 입력에 대해 정규화(평균 = 0, 분산 = 1이 되도록)하여 입력값의 범위를 0을 중심으로 하도록 변환

+) 분산을 컨트롤하는 이유

• 평균이 0이더라도 입력값들의 변화폭(분산)이 너무 작으면
  → 활성화 함수의 output 또한 변화 자체가 너무 작아 서로 다른 data item들에 대한 차이를 신경망이 구분하기 어렵다
• 분산이 너무 크면
  → 입력값의 범위를 제한하는 원래 목표에 어긋나게 된다
  
  

보통 Fully connected layer(FC layer) 다음에 Batch normalization layer(BC layer)를 수행하는데, 평균 = 0, 분산 = 1로 정규화하다 보면 두 layer 사이에서 신경망이 잘 추출한 정보를 잃어버리는 문제가 발생할 수도 있다.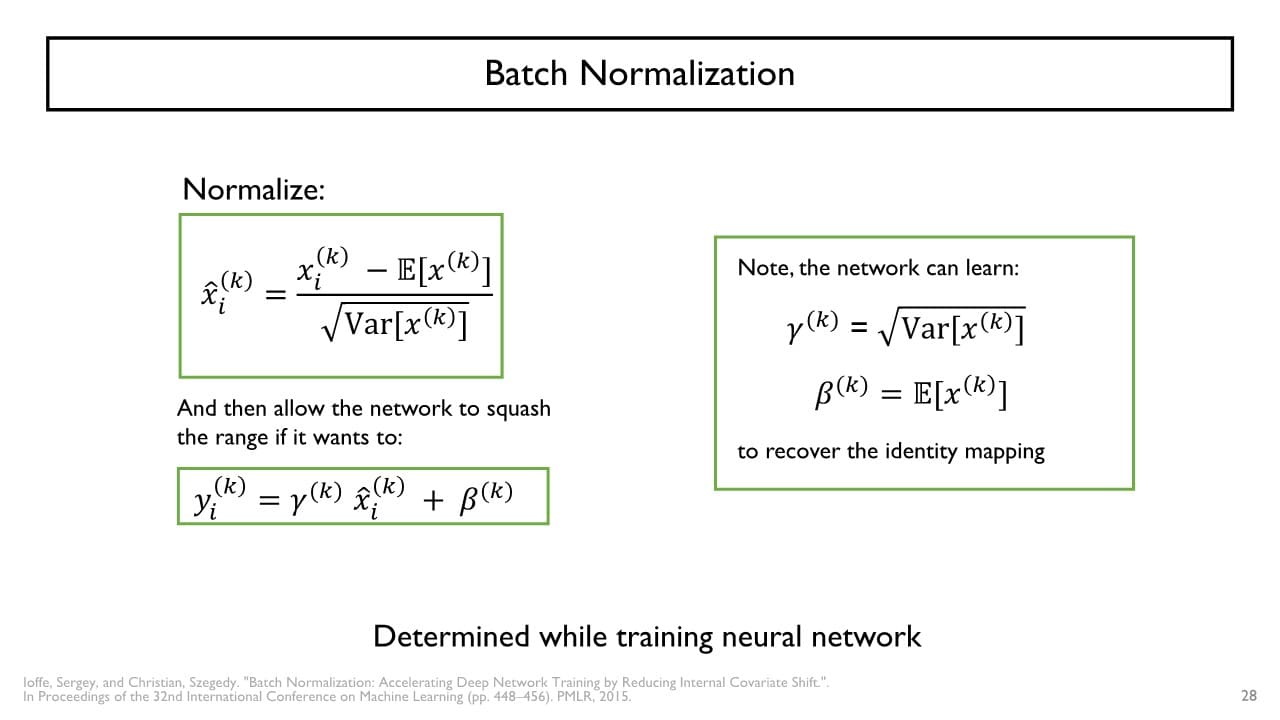Batch normalization의 2번째 단계에서 이때 잃어버린 정보를 스스로 복원할 수 있다.
(= 해당 데이터가 가지는 고유의 평균과 분산 복원 가능)

따라서 Batch Normalization의 전체적인 과정은 아래와 같다.