Module 4. 『딥러닝(Deep Learning)』 1. Introduction to Deep Neural Networks

📍 강의 자료 출처 : LG Aimers

1. 심층신경망(deep neural networks)의 기본 동작 과정

Deep Learning

: 기계학습 방식의 일종으로, 뉴런 혹은 신경세포와 그들간의 (연결 관계)망을 본따 수학적인 인공지능으로 만든 알고리즘

자연어 처리나 컴퓨터비전 분야에서 많이 활용되고 있다.

이 딥러닝이 좋은 성능을 보이기 위해서는 다음 3가지 조건을 갖추어야 한다.
1. 많은 양의 학습데이터
2. 높은 사양의 GPU 하드웨어
3. 진보된 딥러닝 알고리즘

Perceptron

perceptron은 입력 $x$를 가중치 $w$와 곱해 가중합을 만들고
이 값이 활성화 함수를 거쳐 최종 출력 신호 $y$를 만들어낸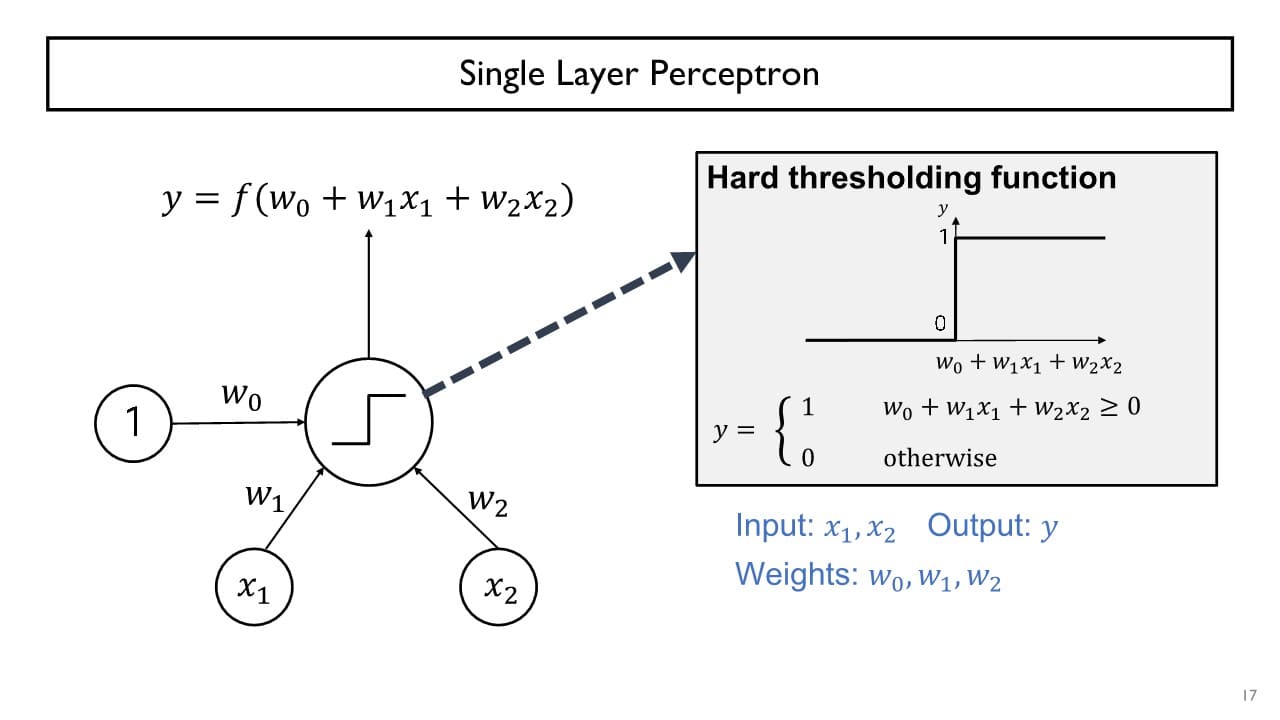다.perceptron을 통해 AND gate, OR gate 문제를 쉽게 해결할 수 있다.
cf> XOR gate는 single layer perceptron으로는 풀 수 없다.
+) multi-layer perceptron의 경우, input layer는 default로 주어지는 정보이기 때문에 이를 제외한 hidden layer의 수 + ouput layer 1개만큼의 층을 쌓는다고 생각하면 된다.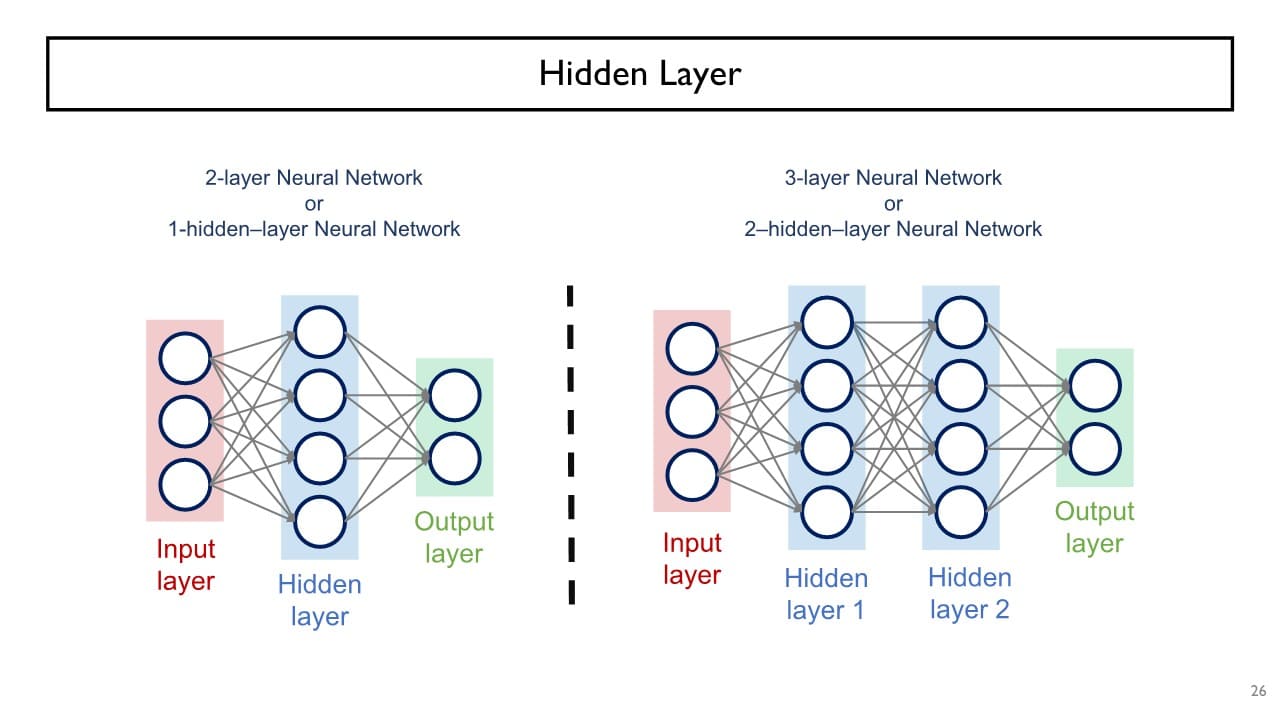

decision boundary
: 입력과 가중치의 선형결합 $= 0$ 이 되는 직선

• 선형결합의 값 > 0 → 출력 = 1
• 선형결합의 값 ≤ 0 → 출력 = 0
  
  ⇒ input feature space는 decision boudary에 의해 양분되고,
  양분된 두 영역 중 한 쪽의 최종 output = 1 / 나머지 한 쪽의 최종 output = 0이 된다.

Forward Propagation

$a_j^{(i)}$
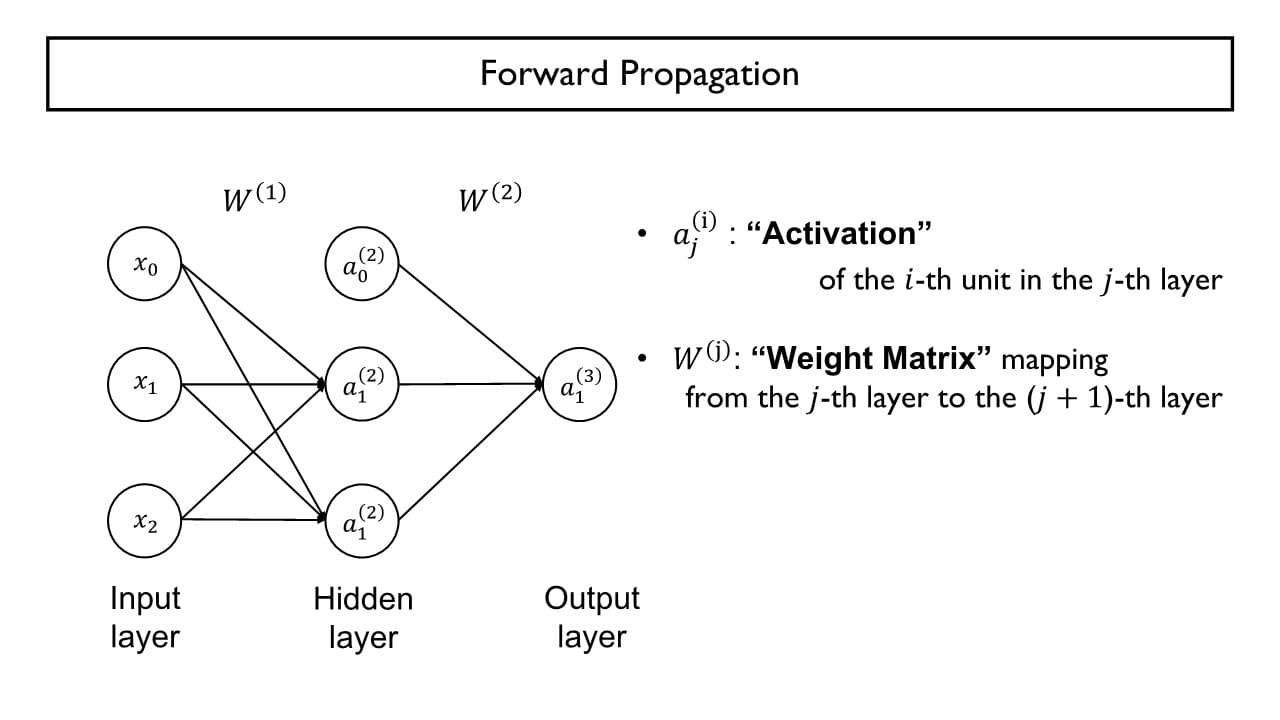
: 특정 layer에서의 특정 뉴런의 출력 값을 activation이라는 의미로 표현한다.
아랫첨자 $j$는 layer, 윗첨자 $i$는 layer 내의 몇번째 노드냐를 의미하는 index로 사용한다.

$W^(i)$
: 계층별 가중치들의 모음체인 가중치 행렬
윗첨자 $j$는 특정 layer를 나타낸다.

가중치와 입력의 선형결합 값이 sigmoid function(= logistic function)을 거쳐 0 ~ 1 사이의 어떤 실수값을 최종 ouput으로 나오게 된다.

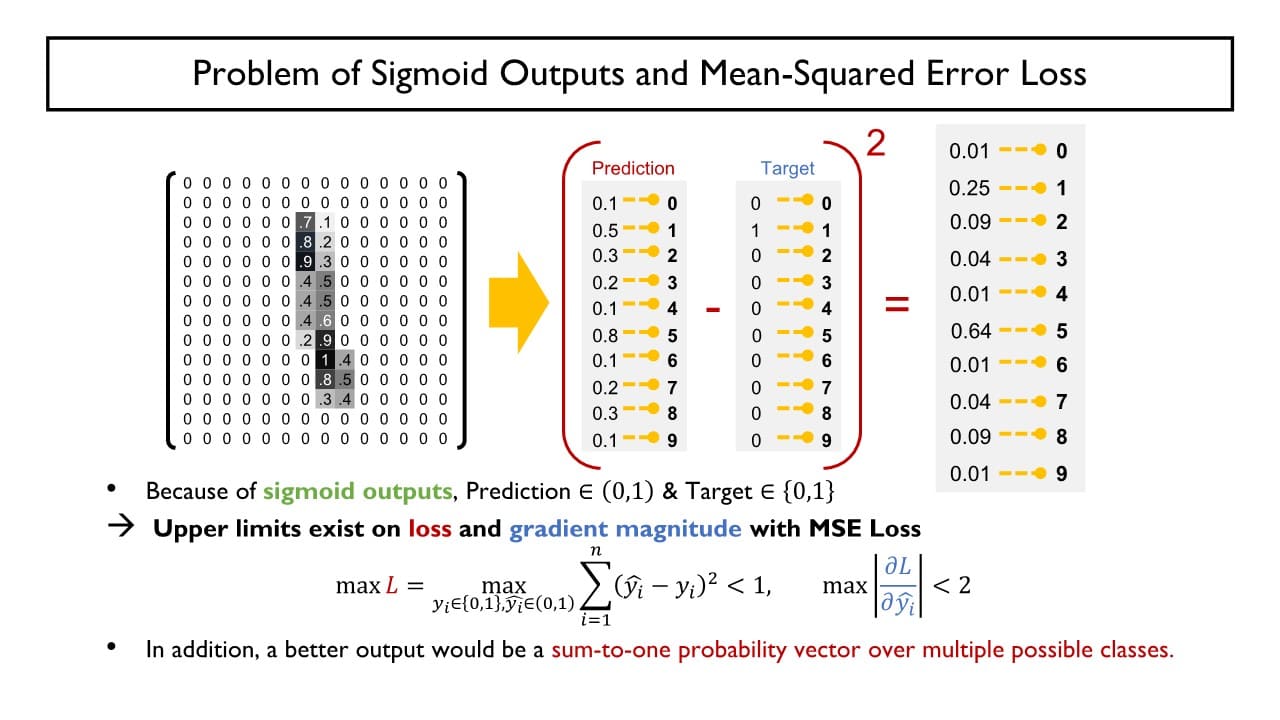
MSE Loss 방식을 사용하게 되면 예측값과 실제 정답 사이의 차가 최대 1까지만 가능하기 때문에 미분하면 gradient가 작아 학습이 더디다는 단점이 있다.
이러한 문제점을 해결하고 출력값 확률 분포(출력 벡터)의 합이 1이 되도록 만들기 위해 Softmax Layer를 도입했다.

Softmax Layer

• softmax layer의 입력
  : 전 layer에서의 행렬곱에 의한 결과로, $[-\infty, \infty]$까지의 다양한 값을 가질 수 있다.
  확률분포의 합을 1로 변환하기 위해 지수함수에 대입하고 지수함수 결과값 간 상대적 비율을 사용한다.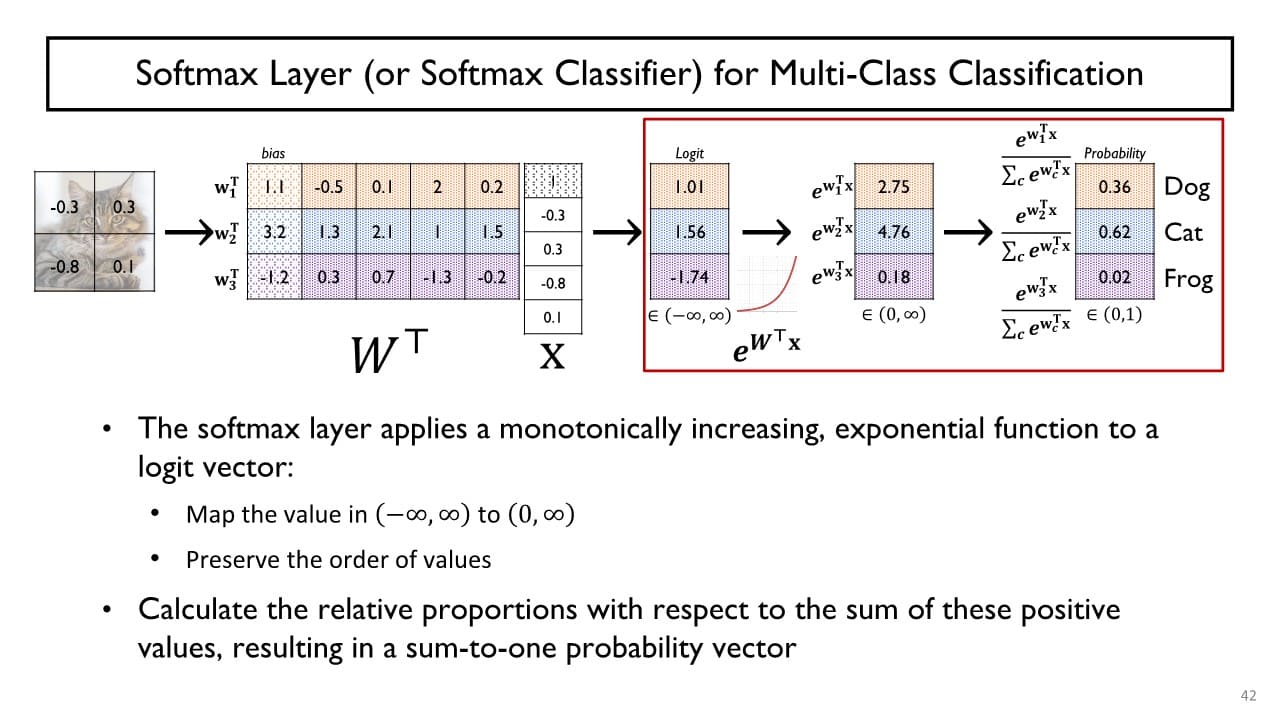softmax layer의 출력 벡터를 softmax loss 혹은 cross-entropy loss에 적용하여 loss function을 계산한다.

  → $-logx$ 그래프를 보면 알 수 있듯 정답 class에 부여된 확률값이 작아질수록 무한히 큰 Loss를 발생시키고 확률 값이 1에 가까울수록 Loss는 0에 가까워진다.

  softmax loss는 다른 class에 부여된 확률값은 고려하지 않는데,
  softmax layer에서 지수함수 결과값 간 상대적 비율을 사용하였기 때문에 정답 class가 1에 가깝게 커질수록 다른 class의 값은 점점 작아지게 되기 때문에 정답 class만을 고려하여 loss function을 정의하게 된다.

  • Logistic regression
    logistic regression 또한 Softmax classifier의 특별한 형태로 볼 수 있다.
    → negative class에 해당하는 가중치는 모두 0으로 고정하고 positive class의 가중치만을 학습을 통해 최적화된 값을 도출해낸다.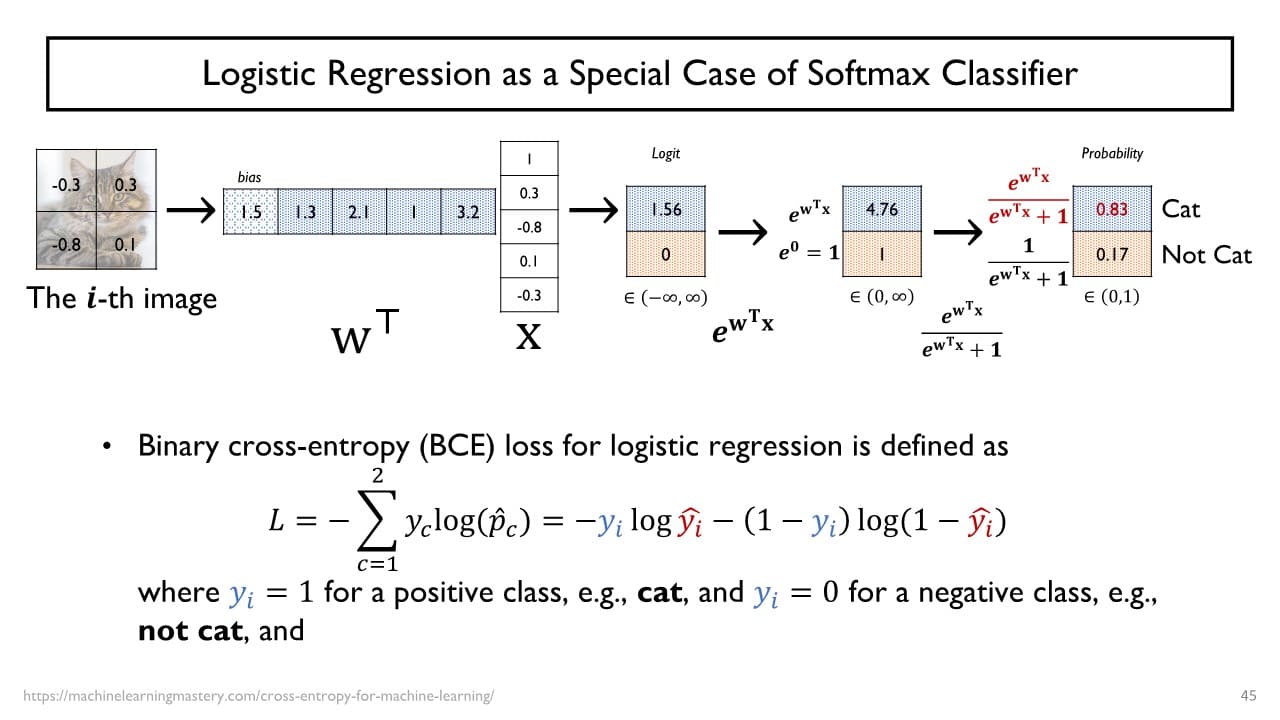이진 분류를 위해 사용하는 logistic regression은 $y_i$가 항상 0 또는 1만을 가지기 때문에 cross-entropy function이 앞서 본 softmax에서의 식과 동일한 결과를 출력하는 것을 확인할 수 있다.