[알고리즘] 빅오 표기법 (Big O Notation)

uxolrv·2022년 9월 6일

algorithm

목록 보기

2/3

📌 코드 시간 재기

코드가 실행되는 데 걸리는 시간을 알 수 있는 가장 쉬운 방법은 내장 되어있는 타이밍 함수를 사용하는 것

function addUpTo1(n) {
    return n * (n + 1) / 2;
}

let time1 = performance.now();
addUpTo(1000000000)
let time2 = performance.now();

console.log(`Time Elapsed: ${(time2 - time1) / 1000} seconds.`) 
// 1000분의 1초 단위로 되어있기 때문에 1000을 나눠 줌

그러나 코드가 실행될 때의 시간을 측정하는 것은 정확도에 문제가 있다.

🚫 기기 사양에 따라 시간이 다르게 측정되기 때문에 정확한 시간을 알 수 없다.
🚫 같은 기기에서도 코드를 실행할 때마다 조금씩 시간이 다르게 기록된다.
🚫 매우 짧은 시간 안에 처리되는 빠른 알고리즘에서는 타이밍 함수가 그런 작은 차이를 정확히 측정하지 못한다.

❗️ 대신에 컴퓨터가 처리해야하는 연산 개수를 세면 된다!
어떤 컴퓨터를 사용하든 그 연산 개수는 변하지 않기 때문에 시간을 측정하는 것보다 정확하다.

✨ 예시1

function addUpTo1(n) {
    return n * (n + 1) / 2;
}

이 경우, n값과는 상관 없이 총 3번 연산한다.
(곱셈 1번 + 덧셈 1번 + 나눗셈 1번)

✨ 예시2

function addUpTo2(n) {
    let total = 0;
    for (let i = 1; i <= n; i++) {
        total += i;
    }
    return total;
}

코드	연산 횟수
`let total = 0`	total 선언 및 할당 (1회)
`let i = 1`	i 선언 및 할당 (1회)
`i <= n`	반복할 때마다 비교 (n회)
`i++`	반복할 때마다 덧셈 (n회)
`i++`	반복할 때마다 할당 (n회)
`total += i`	반복할 때마다 덧셈 (n회)
`total += i`	반복할 때마다 할당 (n회)

5n + 2 번 연산하는 함수로, n이 커질 수록 연산의 개수도 비례적으로 증가한다.

만약 n이 10이라면 ?
n회 반복되는 연산 총 50개 + 반복문 바깥 연산 2개 = 52개

📌 빅오 표기법 Big O Notation

알고리즘의 효율성(시간 복잡도)를 나타낼 때 사용하는 표기법
입력의 크기와 실행 시간 사이의 관계를 뜻한다.

일반적으로 실행시간이 가질 수 있는 최대치, 즉 가장 높은 실행 시간 값을 말한다.

f(n) could be linear (f(n) = n)
➡️ 실행 시간이 선형으로 증가할 수 있다. (n과 함께 증가)
f(n) could be quadratic (f(n) = n²)
➡️ 실행 시간이 n의 제곱일 수 있다. (n과 함께 증가)
f(n) could be constant (f(n) = 1)
➡️ 실행 시간이 상수 일 수 있다. (n이 커져도 실행 시간에는 영향이 없음)
❗️ 실행 시간이 상수인 경우, 단순히 1이라고 표현한다
f(n) could be something entirely different!
➡️ 입력의 크기와 실행시간 사이의 관계가 완전히 다를 수 있다.

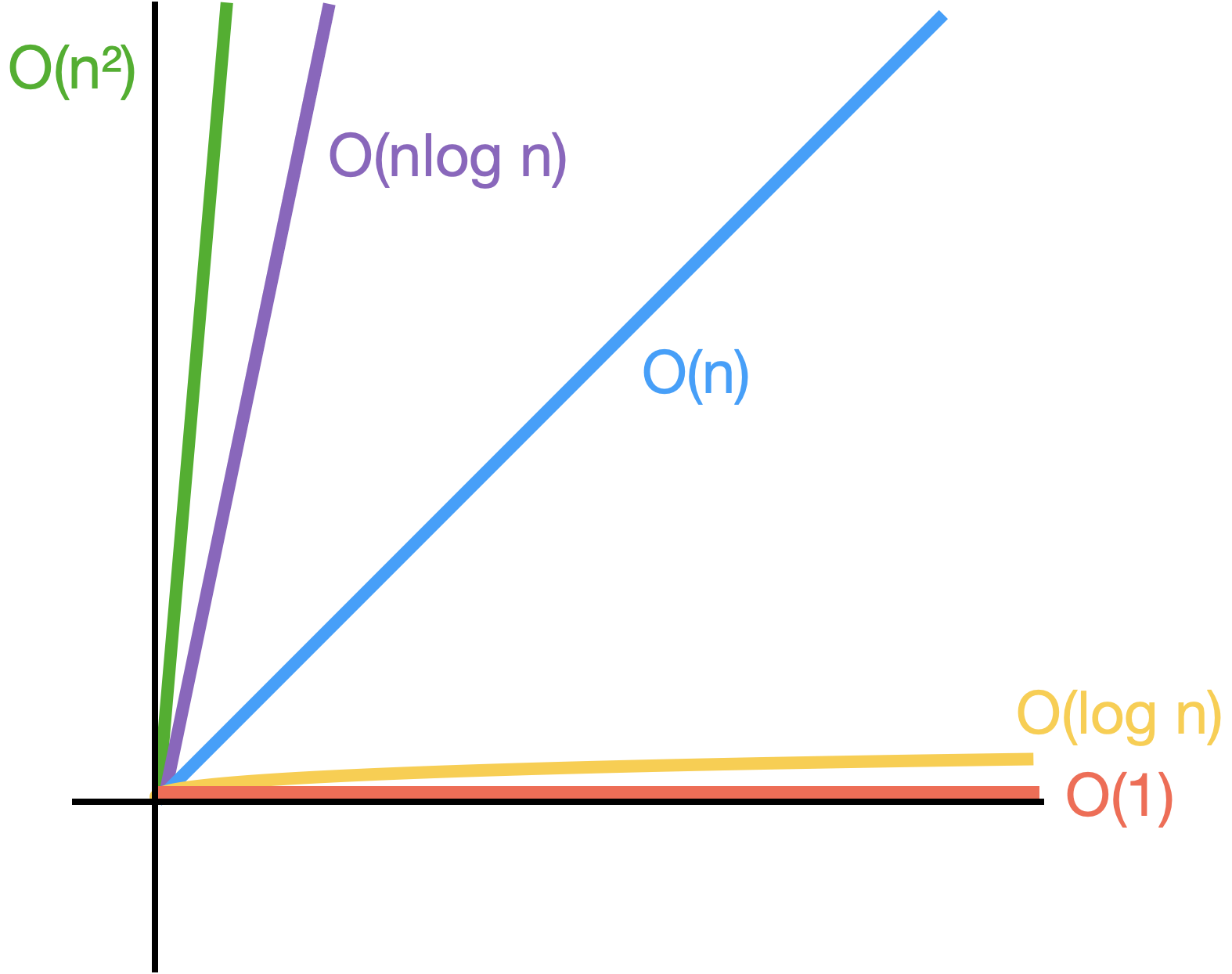
시간복잡도 효율 순
O(1) < O(log n) < O(n) < O(n log n) < O(n²)

💡 `O(1)`

function addUpTo(n) {
    return n * (n + 1) / 2;
}

해당 함수의 경우 언제나 연산이 3개이기 때문에 O(1) 으로 표현할 수 있다.

💡 `O(n)`

function addUpTo(n) {
    let total = 0;
    for (let i = 1; i <= n; i++) {
        total += i;
    }
    return total;
}

해당 함수의 경우 실행 시간이 1:1 비율로 증가하고, 연산의 갯수가 n의 곱과 연결 되어있기 때문에 O(n) 으로 표현할 수 있다.

 function countUpAndDown(n) {
    console.log("Going up!");
    for (let i = 0; i < n; i++) {  // O(n), n이 증가할 수록 반복 횟수가 증가하기 때문에
        console.log(i);
    }
    console.log("At the top!\nGoing down...");
    for (let j = n - 1; j >= 0; j--) {  // O(n), n이 증가할 수록 반복 횟수가 증가하기 때문에
        console.log(j);
    }
    console.log("Back down. Bye!");
}

반복문이 2개이기 때문에 O(2n) 이라고 생각할 수 있지만 빅오 표기법으로는 O(n) 으로 표기 한다.
❗️ 같은 비율로 증가하고 있다면 2n이든, 5n이든, 10n이든 전부 O(n) 로 표기

💡 `O(n²)`

function printAllPairs(n) {
  for (var i = 0; i < n; i++) {  // O(n)
    for (var j = 0; j < n; j++) {  // O(n)
      console.log(i, j)
    }
  }
}

O(n) 연산 안에 O(n) 연산
= O(n * n)
= O(n²)

n이 커질 수록 실행 시간이 n 제곱의 값으로 증가하므로 O(n²)으로 표기한다.

📌 빅오 표현식 단순화 하기

이 모든 연산들을 다 세는 것은 힘들고, 사실 정확한 갯수가 중요하지 않다는 것을 알 수 있다.
중요한 것은 전체적인 추세!

5n + 2 ===> O(n)

10n이든 1000n이든 중요하지 않음
추세 즉, 실행 시간이 n의 값과 비례한다는 것이 중요하다.

O(2n) ===> O(n)
O(500) ===> O(1)
O(13n²) ===> O(n²)

대략적으로 정확한 큰 그림을 봐야 하므로, 상수는 신경쓰지 않는다.

O(n² + 5n + 8) ===> O(n²)

❗️ 추세를 나타낸 그래프를 아주 먼 우주에서 바라보고 있다고 생각하자.
작고 사소한 것에 신경쓰지 말고 큰 것에 집중해야 한다.

이 때, n제곱에 비해서 5n + 8은 아무 의미가 없다.

이렇게 상수를 없애고 나면, 단순화된 표현식들끼리 비교할 수 있다.

💡 빅오 표현식을 단순화하는 데에 도움을 주는 규칙들

1️⃣ 산술 연산은 상수다. (= 항상 일정한 값을 취한다.)
(덧셈, 뺄셈, 곱셈, 나눗셈을 포함)

컴퓨터에게는 2+2를 처리하는 시간과 1000000+2를 처리하는 시간이 비슷하다.
그러므로 n의 값이 상관이 없는 것 !

2️⃣ 변수에 값을 할당하는 것은 상수다.

3️⃣ 인덱스를 사용해 배열에 접근하거나, 키를 사용해 객체에 접근하는 것 또한 상수다.

4️⃣ 반복문이 있는 경우, 복잡도 = 루프의 길이 * 루프 안에 있는 연산들
0에서 n까지 반복한다면, n이 커질 수록 반복 횟수가 증가
이중 반복문이 있다면, 실행 시간은 n²

✨ 예시 3

function logAtLeast5(n) {
  for (var i = 1; i <= Math.max(5, n); i++) {
    console.log(i);
  }
}

n이 5보다 작다면 5번 반복하고, n이 5보다 크다면 n번 반복하는 함수
n이 커질수록 연산 개수가 n에 비례하여 증가하기 때문에 O(n)

✨ 예시 4

function logAtMost5(n) {
  for (var i = 1; i <= Math.min(5, n); i++) {
    console.log(i);
  }
}

n이 5보다 작다면 n번 반복하고, n이 5보다 크다면 5번 반복하는 함수
n이 커져도 아무런 영향을 주지 않기 때문에 O(1)

📌 공간 복잡도

입력이 커질수록 알고리즘이 얼마나 많은 공간(메모리)을 차지하는 지
입력되는 것을 제외하고 알고리즘 자체가 필요로 하는 공간

boolean, number, undefined, null 타입은 모두 불변 공간
입력의 크기와는 상관 없이 숫자가 1이든 1000이든 모두 불변 공간으로 여긴다.
string 타입은 O(n) 공간이 필요
만약 50자인 문자열이 있다면, 길이가 1자인 문자열보다 50배 더 많은 공간을 차지
array, object 타입은 O(n) 공간이 필요
만약 길이가 4인 배열이 있다면, 길이가 2인 배열보다 2배 더 많은 공간을 차지

예시

function sum(arr) {
  let total = 0;
  for (let i = 0; i < arr.length; i++) {
    total += arr[i]
  }
  return total
}

공간을 차지하는 부분
let total = 0
let i = 0

total += arr[i]
새로운 변수를 만드는 것이 아닌, 이미 선언된 변수에 더하는 것
=> 공간은 이미 할당되어 있고, 시간이 더 소요됨

상수 공간이 있는 코드 ===> O(1) 공간
(입력의 크기와는 상관없이 항상 똑같은 공간을 차지)

function double(arr) {
  let newArr = [];
  for (let i = 0; i < arr.length; i++) {
    newArr.push(2 * arr[i]);
  }
  return newArr;
}

각 배열의 요소가 두 배가 된 배열을 리턴하는 함수

입력된 배열의 길이가 10이라면, 새로운 배열에 저장되는 요소가 10개
=> 차지하는 공간은 입력된 배열의 크기와 비례하여 커지게 된다.

O(n) 공간을 차지하는 코드

O(log n)

log2(8) = 3 === 2³ = 8
: 2의 몇승의 값이 8이 되나요?

어떤 이진 로그를 대략 계산하기 위해서는 그 숫자가 1보다 작아지기 전에 2로 나눠지는 횟수를 알아내야 한다.

8 / 2 = 4
4 / 2 = 2
2 / 2 = 1
log(8) = 3

25는 정확하게 2로 나눌 수 없음
25 / 2 = 12.5
12.5 / 2 = 6.25
6.25 / 2 = 3.125
3.125 / 2 = 1.5625
1.5625 / 2 = 0.78125
log(25) ≈ 4.64

<log와 관련있는 알고리즘>
탐색 알고리즘, 효율적인 정렬 알고리즘, 재귀
재귀는 시간이 아닌, 공간 복잡도와 관련

총 정리

알고리즘의 성능을 분석하기 위해서는 빅오표기법을 사용한다.
입력의 크기, 전체적인 추세와 관련됨
빅오를 통해 시간 복잡도, 공간 복잡도에 대한 이해를 높일 수 있다.
정확도가 아닌 전체적인 추세를 중요시 한다.
빅오로 측정되는 알고리즘의 시간과 공간 복잡도는 하드웨어에 영향을 받지 않는다.
(빅오는 실행될 연산의 갯수를 따지기 때문)

객체는 언제 사용할까?

정렬되어 있을 필요가 없을 때
빠른 접근, 입력, 제거를 원할 때

배열은 언제 사용할까?

정렬되어 있는 데이터가 필요할 때
빠른 접근, 입력, 삭제를 원할 때

객체의 빅오

입력 : O(1)
제거 : O(1)
탐색 : O(n) (어떤 특정한 정보가 어떤 값에 있는 지 확인하는 것)
접근 : O(1)

객체 메소드의 빅오

메소드	빅오
Object.keys	O(n)
Object.values	O(n)
Object.entries	O(n)
hasOwnProperty	O(1)

배열의 빅오

입력 : it depends
제거 : it depends
탐색 : O(n)
접근 : O(1)
❗️ 접근
JS에서 10000개의 요소가 있는 배열에서 9000번째 요소를 요청한다 가정했을 때, 0번째부터 9000번째까지 모든 엘리먼트를 하나씩 지나가는 것이 아님! 해당 인덱스로 바로 접근 가능하기 때문에 배열의 길이는 중요하지 않음
❗️ 입력
가장 끝에 추가하는 경우: O(1)
가장 앞에 추가하는 경우: O(n)
인덱스들이 1개씩 밀리기 때문에 엘리먼트마다 인덱스를 새로 배정하는 작업이 필요함
❗️ 제거
가장 끝에 있는 요소를 제거하는 경우: O(1)
가장 앞에 있는 요소를 제거하는 경우: O(n)
인덱스들이 앞으로 1개씩 당겨져야 하기 때문에 엘리먼트마다 인덱스를 새로 배정하는 작업이 필요함

효율적인 측면에서 봤을 때, 앞에서 추가/제거하는 것보다 끝에서 추가/제거하는 것이 더 효율적이다.
그러므로 효율을 생각한다면, 배열 앞에 데이터를 추가/제거하는 것은 최대한 피하는 것이 좋다.

배열 메소드의 빅오

메소드	빅오
push	O(1)
pop	O(1)
shift	O(n)
unshift	O(n)
concat	O(n)
slice	O(n)
splice	O(n)
sort	O(n * log n)
forEach/map/filter/reduce/etc.	O(n)

slice : 걸리는 시간은 복사하는 엘리먼트 개수만큼 증가

uxolrv

안녕하세연🙋 프론트엔드 개발자입니다

이전 포스트

[알고리즘] 타일링 알고리즘 문제

다음 포스트

[알고리즘] 빅오 표기법 (Big O Notation)

algorithm

📌 코드 시간 재기

✨ 예시1

✨ 예시2

📌 빅오 표기법 Big O Notation

💡 `O(1)`

💡 `O(n)`

💡 `O(n²)`

📌 빅오 표현식 단순화 하기

💡 빅오 표현식을 단순화하는 데에 도움을 주는 규칙들

✨ 예시 3

✨ 예시 4

📌 공간 복잡도

O(log n)

총 정리

객체는 언제 사용할까?

배열은 언제 사용할까?

객체의 빅오

객체 메소드의 빅오

배열의 빅오

배열 메소드의 빅오

[알고리즘] 타일링 알고리즘 문제

[알고리즘] 최대 공약수, 최소 공배수 찾기 (유클리드 호제법)

0개의 댓글

[알고리즘] 빅오 표기법 (Big O Notation)

algorithm

📌 코드 시간 재기

✨ 예시1

✨ 예시2

📌 빅오 표기법 Big O Notation

💡 O(1)

💡 O(n)

💡 O(n²)

📌 빅오 표현식 단순화 하기

💡 빅오 표현식을 단순화하는 데에 도움을 주는 규칙들

✨ 예시 3

✨ 예시 4

📌 공간 복잡도

O(log n)

총 정리

객체는 언제 사용할까?

배열은 언제 사용할까?

객체의 빅오

객체 메소드의 빅오

배열의 빅오

배열 메소드의 빅오

[알고리즘] 타일링 알고리즘 문제

[알고리즘] 최대 공약수, 최소 공배수 찾기 (유클리드 호제법)

0개의 댓글

💡 `O(1)`

💡 `O(n)`

💡 `O(n²)`