★N-Queen★

N-Queens - LeetCode

★다시 풀어보기★ (재도전도 실패 → 3트만에 성공ㅠㅠ → 꼭 다시 풀어보기)

과거 기록(이전에 풀려했는데 결국 못풀었음 → 아이디어가 생각이 안나서 포기)

'''
아이디어
각 퀸을 다양하게 배치했을때
숫자가 0 인(즉, 한번도 공격로로 설정되지 않은곳) 곳이 퀸을 놓을 수 있는 자리다.

n^2 C n 가지 경우의 수 중 빈칸이 몇개인지 카운팅 
만약 빈칸이 n 개 이상 x 이면 x C n 이 정답
만약 n 개 이하면 0개

시간복잡도
n은 최대 12

총 12*12 = 144칸

144C12 가지 경우의 수 중 빈칸이 몇개인지 카운팅

자료구조

'''

def solution(n):
    answer = 0
    l = [0] * n
    print(l)
    return answer

접근 방법 [필수 작성]

제한 조건 확인

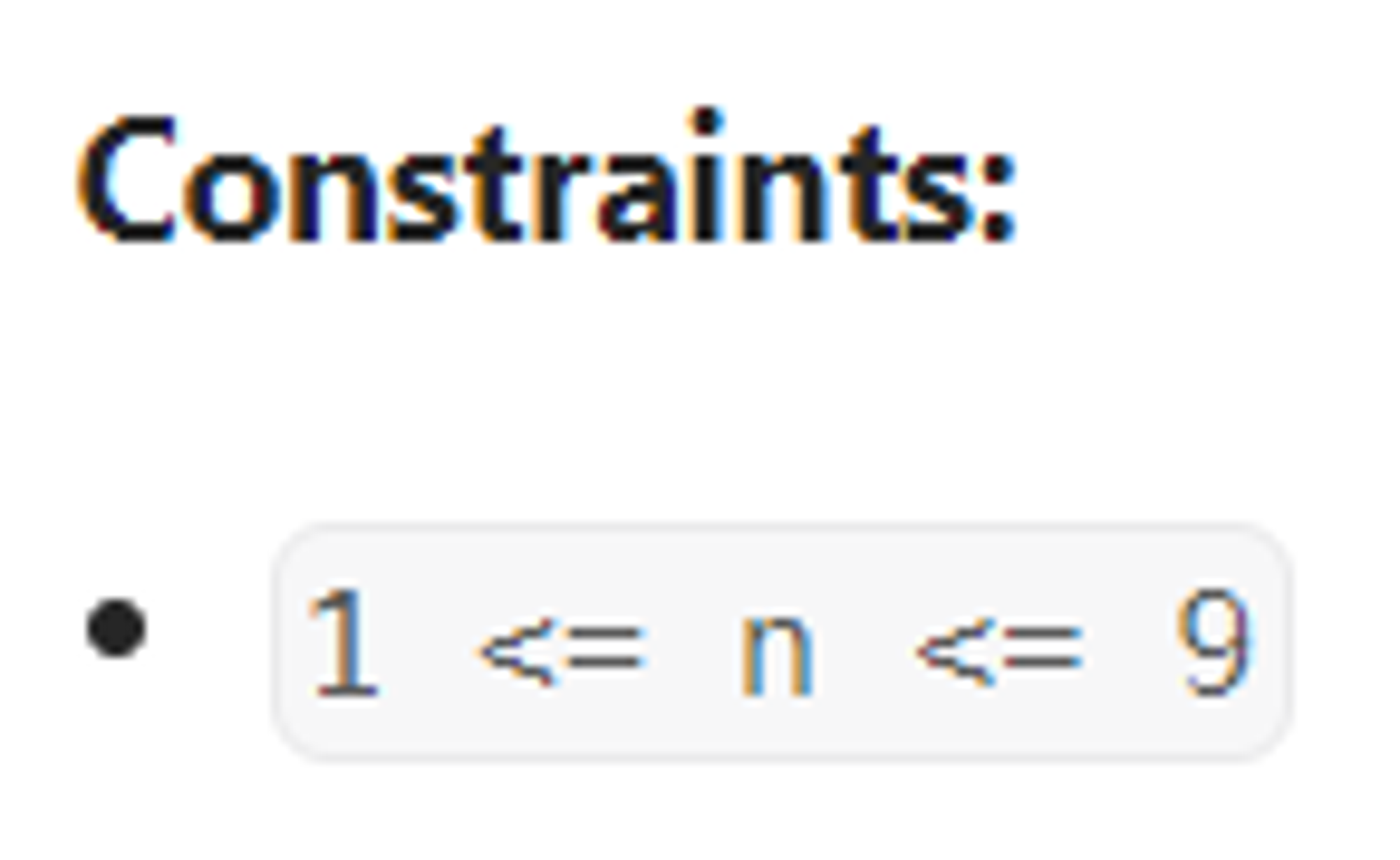
• 가장 복잡한 경우는 99 보드에 퀸 9개를 놓는 경우의 수 탐색 → 81C9 → 818079…7372 / 9! → 910 → 79787573361911 → ~~ 80^4 40 20 10 = 16001600*8000 → 시간 초과 → 완전탐색은 아니고 어느정도 조건을 넣어 배제하는 경우를 만들어주어야 함.
• 재귀적으로 퀸을 보드에 놓다가, 더 이상 놓을 수 없을때 백트래킹
• 만약 다 놓았다면, 해당 결과 저장

코드 구현 [필수 작성]

첫번째 시도 코드

#10시 시작 -> 

class Solution:
    def solveNQueens(self, n: int) -> List[List[str]]:
        result = []
        board = ["."*n for _ in range(n)]
        diagonal_defer = [(-1,-1),(-1,1),(1,-1),(1,1)]
        num_Q = 0

        def check_valid(board,r,c):
            for i in range(n):
                if board[i][c] == "Q":
                    return False
                if board[r][i] == "Q":
                    return False
                for dx,dy in diagonal_defer:
                    new_r = i*dy + r
                    new_c = i*dx + c
                    if 0 <= new_r <= n-1 and 0 <= new_c <= n-1:
                        if board[new_r][new_c] == "Q":
                            return False
            return True

        def backtrack(board,index):
            nonlocal num_Q
            #print(board)

            if index > n*n-1:
                if num_Q < n:
                    return
                elif num_Q == n:
                    result.append(board[:])
                    return
            
            for i in range(index,n*n):
                row = i//n
                col = i%n
                if board[row][col] == ".":
                    if check_valid(board,row,col):
                        board[row] = board[row][:col]+"Q"+board[row][col+1:]
                        num_Q += 1
                        backtrack(board,i+1) #(i//n)+n
                        board[row] = board[row][:col]+"."+board[row][col+1:]
                        num_Q -= 1
                    else:
                        backtrack(board,i+1)
            
        backtrack(board,0)

        return result

[문제점]

불필요한 재귀가 발생 → 한개줄에 Q 이 놓이면 반드시 다음줄에 그 다음 Q이 놓여야함, 그런데 backtrack(board,i+1) 바로 그 다음칸에서 이어서 진행해주고 있음

2번째 시도 코드

#10시 시작 -> 

class Solution:
    def solveNQueens(self, n: int) -> List[List[str]]:

        diagonal_defer = [(-1,-1),(-1,1)] #(1,-1),(1,1) 는 필요없음 이전에 놓은것들에 대해서 겹치는 것만 생각하면 됨
        num_Q = 0

        def check_valid(board,r,c):
            for i in range(n):
                if board[i][c] == "Q":
                    return False
                for dy,dx in diagonal_defer:
                    new_r = i*dy + r
                    new_c = i*dx + c
                    if 0 <= new_r <= n-1 and 0 <= new_c <= n-1:
                        if board[new_r][new_c] == "Q":
                            return False
            return True
        
        # board = [".Q..","...Q","....","..Q."]
        # print(check_valid(board,2,0))
        # print(check_valid(board,2,1))

        # 해설코드 참고해서 짠 코드
        # def backtrack(board,row_index):
        #     if row_index == n:
        #         res.append(["".join(row) for row in board])
        #         return True
            
        #     for col_index in range(n):
        #         if check_valid(board,row_index,col_index):
        #             board[row_index][col_index] = "Q"
        #             backtrack(board, row_index+1)
        #             board[row_index][col_index] = "."

        # res = []
        # board = [["." for _ in range(n)] for _ in range(n)]
        # backtrack(board,0)

        # 내가 직접 짠 코드
        def backtrack(board,row_index):

            if row_index == n:
                res.append(["".join(row) for row in board])
                return True
            
            for col_index in range(n):
                row,col = row_index, col_index
                if board[row][col] == ".":
                    if check_valid(board,row,col):
                        board[row] = board[row][:col]+"Q"+board[row][col+1:]
                        if backtrack(board,row_index+1): #바로 다음줄 
                            return True
                        board[row] = board[row][:col]+"."+board[row][col+1:]
            return False
            
        res = []
        board = ["."*n for _ in range(n)]
        backtrack(board,0)

        return res

→ 문제점

이 문제는 Sudoku Solver 처럼 1개의 유일해를 찾는 문제가 아님. 가능한 모든 경우에 대해서 해를 찾는 경우임. 그래서 모든 경우에 대해서 완전탐색을 진행 후 정답 후보들을 모두 result 리스트에 append 해주어 return 해주어야함. 그런데,

if backtrack(board,row_index+1): #바로 다음줄 
	return True

이렇게 적어주면, 정답 한개를 고정해버리고 그 정답에 대해서만 파고듬. 즉 모든 경우에 대한 완전탐색이 진행이 안됨.

최종 코드 (3트만에 성공 ㅠㅠ)

class Solution:
    def solveNQueens(self, n: int) -> List[List[str]]:

        diagonal_defer = [(-1,-1),(-1,1)] #(1,-1),(1,1) 는 필요없음 이전에 놓은것들에 대해서 겹치는 것만 생각하면 됨
        num_Q = 0

        def check_valid(board,r,c):
            for i in range(n):
                if board[i][c] == "Q":
                    return False
                for dy,dx in diagonal_defer:
                    new_r = i*dy + r
                    new_c = i*dx + c
                    if 0 <= new_r <= n-1 and 0 <= new_c <= n-1:
                        if board[new_r][new_c] == "Q":
                            return False
            return True
        
        # board = [".Q..","...Q","....","..Q."]
        # print(check_valid(board,2,0))
        # print(check_valid(board,2,1))

        # 해설코드 참고해서 짠 코드
        # def backtrack(board,row_index):
        #     if row_index == n:
        #         res.append(["".join(row) for row in board])
        #         return True
            
        #     for col_index in range(n):
        #         if check_valid(board,row_index,col_index):
        #             board[row_index][col_index] = "Q"
        #             backtrack(board, row_index+1)
        #             board[row_index][col_index] = "."

        # res = []
        # board = [["." for _ in range(n)] for _ in range(n)]
        # backtrack(board,0)

        # 내가 직접 짠 코드
        def backtrack(board,row_index):

            if row_index == n:
                res.append(["".join(row) for row in board])
                return True
            
            for col_index in range(n):
                row,col = row_index, col_index
                if board[row][col] == ".":
                    if check_valid(board,row,col):
                        board[row] = board[row][:col]+"Q"+board[row][col+1:]
                        backtrack(board,row_index+1) #바로 다음줄 
                        board[row] = board[row][:col]+"."+board[row][col+1:]
            
        res = []
        board = ["."*n for _ in range(n)]
        backtrack(board,0)

        return res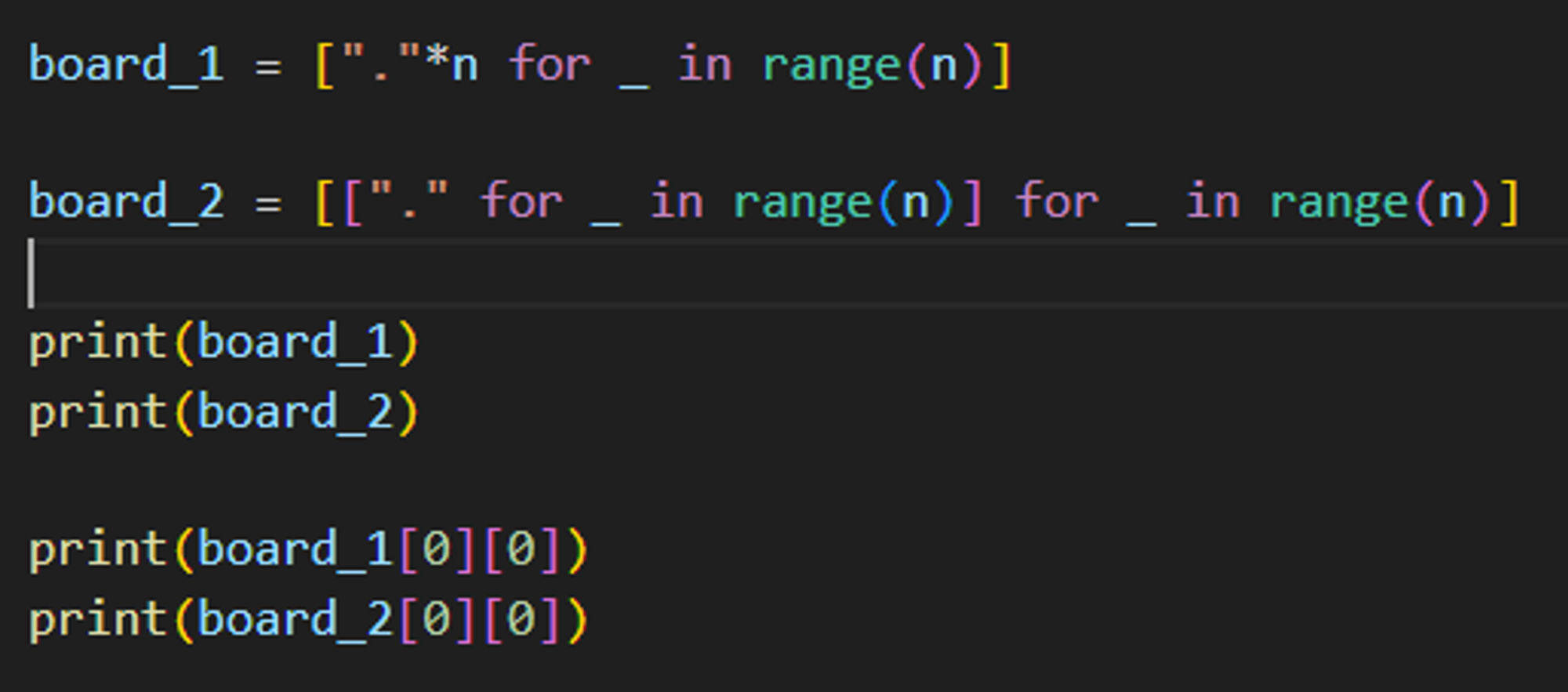

배우게 된 점 [ 필수 X ]

1. 원본이 아닌 복사본을 return 해야하는 이유

board 를 그냥 리턴하게 될 경우

한개의 board 에 대해서 삽입, 삭제를 진행하는 재귀가 모두 완료되면 해당 보드는 [’.’,’.’,’.’,’.’] 만 출력하게 됨. 왜냐면 모든 경우에 대해서 완전탐색한 후 Q를 다시 다 . 으로 바꿔주기 때문에.

그래서 반드시 후보 정답에 대해서 복사본을 result 리스트에 추가해준 후, result 리스트를 반환해야한다.

1. board 를 ["."*n for _ in range(n)] 로 초기화하는 것과 [["." for _ in range(n)] for _ in range(n)] 로 초기화 하는 것의 차이

전자로 초기화할 경우

board[row_index][col_index] = "Q” → 에러

board[row] = board[row][:col]+"Q"+board[row][col+1:] → 와 같이 조잡한 방식으로 변경해주어야 함

후자로 초기화할 경우

board[row_index][col_index] = "Q” → 가능

후자의 경우 리스트의 원소로 접근하기 때문에 리스트내의 원소를 바꾸는 개념으로 바로 assign 이 가능하지만, 전자의 경우 하나의 string 이 반환되어 버리기 때문에 assign 이 불가능하다.

실제로

다음과 같은 에러가 뜬다.

그래서 해설코드는 후자와 같은 트릭을 활용하고 나중에 Join 하는 식으로 더 가독성이 좋은 코드를 작성했다.

질문 [ 필수 X ]

자유 형식

피드백 [ 코치 작성 ]

불필요한 재귀가 발생하고 있습니다. 또한 재귀 함수의 종료 조건도 수정이 필요할 듯 합니다.