★Sudoku Solver★(100/100)
★다시 풀어봐야할 문제★ (해설코드보고 정답 맞춤 나중에 다시 풀어보기) → 재귀 구현시 껍질 두개까고 나오는 아이디어 까먹지 말기!
접근 방법 [필수 작성]
제한 조건 확인
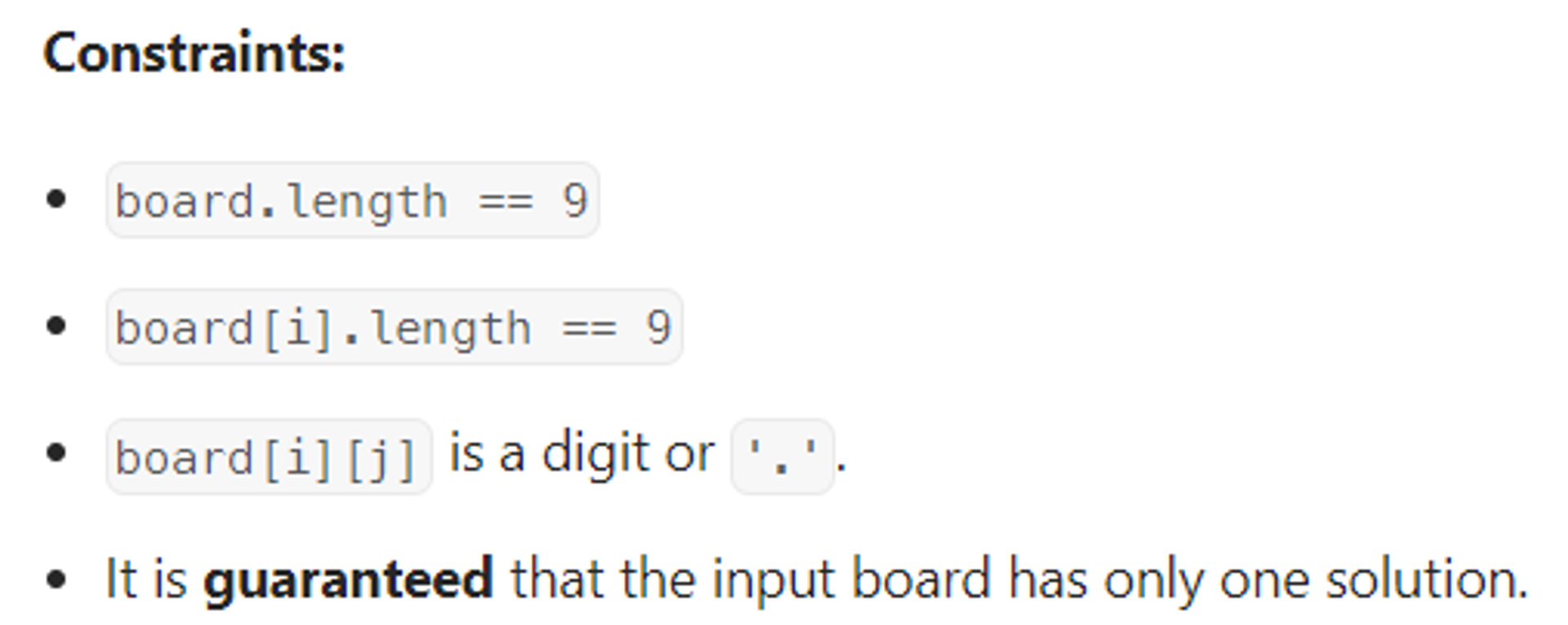
- 반드시 하나의 답만 가지므로 중복 우려 x
- 보드가 9*9 로 한정되어 있으므로 굉장히 작은 숫자이므로 완전탐색으로 접근 가능성
- 재귀로 구현시 시간복잡도 계산 어려움…
아이디어
그냥 단순히 스도쿠 푸는 문제임
사람이 스도쿠를 어떻게 푸는지 그 flow 를 생각해보면 될 것 같음
완탐으로 풀어도 시간복잡도 괜찮은지 확신을 얻어야함
각 격자칸 별, column 별, row 별 container 를 만들기
서로 간의 관계 파악하면서 숫자 지워나가기
반드시 특정 숫자가 놓여야 하는 칸 발견하기
어느칸부터 탐색을 시작해야하지?
정보의 부족으로 특정칸에 들어갈 수 있는 숫자의 경우의수가 많을 때는 어떻게 하지?
- 그냥 단순하게 앞쪽칸부터 1,2,3,4,5,6,7,8,9 중에 가능한 숫자 넣어서 계속 진행하다가 더 진행 불가능할 때, 재귀로 빠져나오는 식으로 구현
- 각 col, row, box 에 같은 숫자가 있는지 없는지 판별하는 함수 작성해주면 좋음
코드 구현 [필수 작성]
시간 초과 오류 코드
#7시 50분 시작 -> 8시 50분 포기
class Solution:
def solveSudoku(self, board: List[List[str]]) -> None:
num_list = [str(i) for i in range(1,10)]
final_board = []
dot_count = 0
for row in board:
for elem in row:
if elem == ".":
dot_count += 1
#print(num_list)
def is_in_row(num,index):
if num in board[index]:
return True
return False
def is_in_col(num,index):
for i in range(9):
if num == board[i][index]:
return True
return False
def is_in_box(num,index):
for row in range((index//3)*3,(index//3)*3+3):
for col in range((index%3)*3,(index%3)*3+3):
if num == board[row][col]:
return True
return False
def can_insert(num,row_index,col_index,box_index):
if not (is_in_row(num,row_index) or is_in_col(num,col_index) or is_in_box(num,box_index)):
return True
return False
def get_box_index(row_index,col_index):
return (row_index//3)*3 + (col_index//3)
def backtrack(start):
nonlocal board
nonlocal final_board
nonlocal dot_count
if dot_count == 0:
final_board = board[:]
return
for row in range(start//9,9):
for col in range(start%9,9):
if board[row][col] == ".":
for num in num_list:
#print(num)
if can_insert(num,row,col,get_box_index(row,col)):
board[row][col] = num
dot_count -= 1
backtrack(start+1)
board[row][col] = "."
dot_count += 1
backtrack(0)
board = final_board
return
"""
Do not return anything, modify board in-place instead.
"""
can_insert(num,row,col,get_box_index(row,col) 에서 모든 숫자에 대해서 삽입 가능 연산을 진행해서 연산수가 엄청나게 많아지는 것으로 예상.. 그런데 내가 알기로… python 은 True or ?? or ?? 인 경우 ??를 연산하지 않고 바로 True 를 반환하는 것으로 알고 있는데 왜 연산수가 많아지는지 잘 모르겠음...
수정코드 ( 재귀 껍질 두번 까고 나오는거 기억해!!! )
#7시 50분 시작 -> 8시 50분 포기
class Solution:
def solveSudoku(self, board: List[List[str]]) -> None:
final_board = []
dot_count = 0
for row in board:
for elem in row:
if elem == ".":
dot_count += 1
def is_in_row(num,index):
if num in board[index]:
return True
return False
def is_in_col(num,index):
for i in range(9):
if num == board[i][index]:
return True
return False
def is_in_box(num,index):
for row in range((index//3)*3,(index//3)*3+3):
for col in range((index%3)*3,(index%3)*3+3):
if num == board[row][col]:
return True
return False
def can_insert(num,row_index,col_index,box_index):
if is_in_row(num,row_index) or is_in_col(num,col_index) or is_in_box(num,box_index):
return False
return True
def get_box_index(row_index,col_index):
return (row_index//3)*3 + (col_index//3)
# 해설코드 참고해서 다시 짠 코드
# def backtrack(board, index):
# if index == 81:
# return True
# r,c = index//9, index%9
# if board[r][c] == ".":
# for num in map(str,range(1,10)):
# if can_insert(num,r,c,get_box_index(r,c)):
# board[r][c] = num
# if backtrack(board,index+1):
# return True
# board[r][c] = "."
# return False
# else:
# return backtrack(board, index+1)
# 해설코드 참고해서 내가 짠 코드 수정본
def backtrack(board, start):
nonlocal dot_count
if dot_count == 0:
return True
for row in range(start//9,9):
for col in range(start%9,9):
if board[row][col] == ".":
for num in map(str,range(1,10)):
#print(num)
if can_insert(num,row,col,get_box_index(row,col)):
board[row][col] = num
dot_count -= 1
if backtrack(board, start+1):
return True
board[row][col] = "."
dot_count += 1
return False
else:
return backtrack(board, start+1)
backtrack(board, 0)
"""
Do not return anything, modify board in-place instead.
"""
배우게 된 점 [ 필수 X ]
def backtrack(start):
nonlocal board
nonlocal final_board
nonlocal dot_count
if dot_count == 0:
final_board = board[:]
return
for row in range(start//9,9):
for col in range(start%9,9):
if board[row][col] == ".":
for num in num_list:
#print(num)
if can_insert(num,row,col,get_box_index(row,col)):
board[row][col] = num
dot_count -= 1
backtrack(start+1)
board[row][col] = "."
dot_count += 1껍질 1번만 까고 나와서
스도쿠 칸에 1~9 숫자를 넣을 수 있던 없던
9^n 모든 경우수를 끝까지 다 탐색해서
시간초과가 나는 코드
def backtrack(board, start):
nonlocal dot_count
if dot_count == 0:
return True
for row in range(start//9,9):
for col in range(start%9,9):
if board[row][col] == ".":
for num in map(str,range(1,10)):
#print(num)
if can_insert(num,row,col,get_box_index(row,col)):
board[row][col] = num
dot_count -= 1
if backtrack(board, start+1):
return True
board[row][col] = "."
dot_count += 1
return False
else:
return backtrack(board, start+1)껍질을 2번 까고 나오는 재귀함수
스도쿠 정답인 숫자가 나오면 계속 해보고
정답이 아닌 숫자 (즉, 1~9 아무것도 넣을 수 없는칸) 이 나오면 False 를 return 후 중단하고 backtracking 을 실행하는 재귀함수
상당한 오답의 경우의 수를 굳이 다 계산해보지않고 줄여줌으로써 실제 9^n보다 훨씬 적은 연산 안에 스도쿠 정답을 찾을 수 있게 됨
스도쿠 게임은 대표적인 NP-complete 문제 중 하나다. NP-complete 문제는 다항 시간안에 해결되지 않는 것으로 알려져 있다. 다만, 특정칸에 정답을 기입할 경우 그 외의 칸들의 경우의 수가 상당수 제거된다. 그래서 최악의 경우 9^n 의 연산수를 하게 될 수도 있다고 생각되지만, 사실은 대부분의 불가능한 경우의 수가 제거되면서 제한시간내에 문제를 풀 수 있게 된다.
질문 [ 필수 X ]
Q1 시간초과이유
Q2 재귀함수의 시간복잡도
피드백 [ 코치 작성 ]
재귀 함수의 시간 복잡도는 언제나 계산하기 어렵습니다. 특히 스도쿠의 경우 각각의 칸에 9개의 숫자가 들어갈 가능성이 있다는 점에서 O(9^n)의 시간을 갖는다고 할 수 있지만 스도쿠의 특성상 하나의 칸에 대한 값이 결정되면 다른 수많은 칸에 대해 영향을 미치기에 해당 시간 복잡도가 스도쿠 풀이 알고리즘을 나타낸다고 보기 어렵습니다.
재귀 함수의 시간 복잡도는 의사 결정 트리를 작성하면 그나마 시간 복잡도의 추론에 도움이 됩니다. 하지만 이 또한 계산하기 어려우며 재귀를 사용하는 문제에 대해서는 word search문제에서 말씀드린 것과 같이 큰 차이가 발생하는 시간 복잡도라도 일단 구해보고 해당 시간 복잡도가 10^8을 초과하더라도 백트래킹의 가지치기에서 많은 경우의 수를 배제할 수 있다면 일단 구현해 보시는 것을 추천드립니다.
스도쿠의 시간 복잡도에 대해 더 궁금하시다면 np complete문제에 대해 찾아보시는 것이 도움이 될 것입니다.
