★Longest Valid Parentheses★

Longest Valid Parentheses - LeetCode

★다시풀어봐야할 문제★ (히든케이스 못찾아서 혼자힘으로 못풀었음 100/100)

접근 방법 [필수 작성]

제한 조건 확인

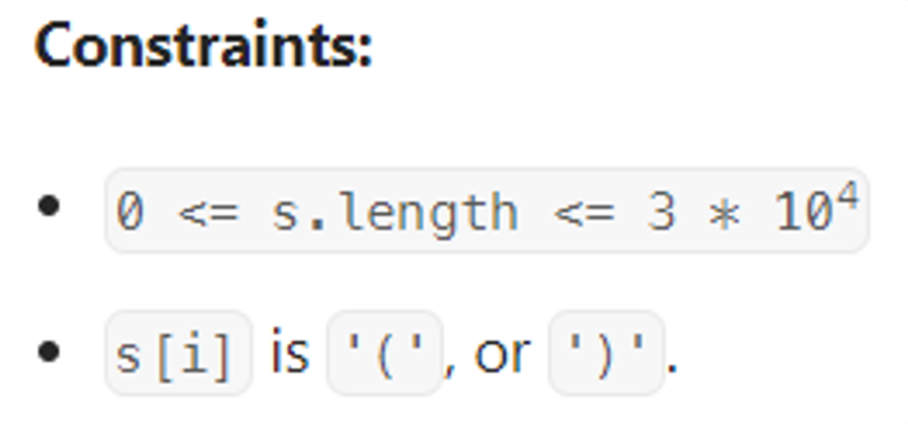
• s 길이 최대 3*10^4 인걸로 봐서 O(n^2) 으로 풀면 안되고 그 이하 시간복잡도 가지는 알고리즘으로 풀어야 함. 선형시간 or nlogn
• 입력값은 무조건 컬리브리킷

아이디어

전형적인 스택 문제

0번째 부터 순차적으로 탐색하는데

만약 잘만들어진거 계속 쌓다가 잘만들어진거 끊기면

그때까지의 누적합 Answer 에 저장

그 뒤로 계속 탐색하는데, 만약 더 큰 완성된 괄호 나오면 answer 교체

어려울 수 있는 포인트는 이상치가 나왔을때 처리를 어떻게 잘해줘서 뒤에 것들 처리하는데 영향을 안주게끔 설계할 것인가?

stack 활용

“(” 나오면 stack 에 괄호 추가

“)” 나오면 현재까지 stack 에 쌓였던 “(” 빼내면서 짝지으면서

curr += 1 해주기

만약 짝 안맞으면, 이제까지 curr 를 max_len 에 저장해주고

다음꺼 curr = 0 만들고 계속 진행

len(s)==0 일때 예외처리 까먹지 말기

시간복잡도

O(n)

연산수 2n (끝까지 갔다가 역탐색으로 돌아옴)

자료구조

코드 구현 [필수 작성]

1차시도

히든테케도 다 통과하려고 확실하게 검사하고 들어갔는데 또 완솔 안됐다 ㅠㅠ

뭐가 문제인지 생각중… → 10분 고민해봐도 코너케이스 생각 안나서 코너케이스 확인함

반례:

"()(()”

( 가 문제의 놈인데 이거를 나중에 되서야 알수가 있음

만약 “(” 가 나오면 현재까지 curr 를 저장하고 다시 새롭게 curr 를 시작하고 stack 이 빌때까지 뽑아보고, 짝이 다 맞으면 아까 저장했던 curr 를 함께 더해서 answer 에 업데이트하고, 그게 아니면 현재 curr 만 answer 에 업데이트 해야됨

#11시 시작 -> 
class Solution:
    def longestValidParentheses(self, s: str) -> int:
        if len(s) == 0:
            return 0
        
        curr = 0
        stack = []
        max_valid = 0

        for i in range(len(s)):
            #print(curr)
            if s[i] == "(":
                stack.append("(")
            elif s[i] == ")":
                if stack:
                    if stack[-1] == "(":
                        stack.pop()
                        curr += 2
                    else: # stack[-1] == ")"
                        if curr:
                            max_valid = max(max_valid,curr)
                            curr = 0
                else:
                    if curr:
                        max_valid = max(max_valid,curr)
                        curr = 0
                    else:
                        pass
        if curr:
            max_valid = max(max_valid,curr)

        return max_valid

2차 시도

딱히 아이디어가 생각이 안나서 그냥 반대편으로도 서치해주고 서로 다르면 작은값을 반환하게 했더니

반례:

"))))())()()(()”

또 같은 문제로 문제가 발생 → 방향전환해봐도 근본적으로 문제를 해결할 수 없음

즉,

"())()()(()” 지금 해결해야할 문제는 내가 문제의 괄호를 늦게 알았을때 어떻게 대처할 것인가?

→ 아예 문제 접근 방식을 갈아엎어야 될 것 같음

→ enumerate 를 사용해서 각 괄호의 인덱스를 저장하고

나중에 알았을때는 추가한 curr 만큼 삭제한것과 새롭게 추가된 것을 모두 answer 에 업데이트 하는 방식

#11시 시작 -> 
class Solution:
    def longestValidParentheses(self, s: str) -> int:
        if len(s) == 0:
            return 0

        def linear_search(s,start,end):
            curr = 0
            stack = []
            max_valid = 0
            inverse = 1
            a = "("
            b = ")"

            if start > end:
                inverse = -1
                a = ")"
                b = "("

            for i in range(start,end,inverse):
                #print(curr)
                if s[i] == a:
                    stack.append(a)
                elif s[i] == b:
                    if stack:
                        if stack[-1] == a:
                            stack.pop()
                            curr += 2
                        else:
                            if curr:
                                max_valid = max(max_valid,curr)
                                curr = 0
                    else:
                        if curr:
                            max_valid = max(max_valid,curr)
                            curr = 0
                        else:
                            pass
            if curr:
                max_valid = max(max_valid,curr)

            return max_valid

        forward = linear_search(s,0,len(s))
        backward = linear_search(s,len(s)-1,-1)

        print(forward)
        print(backward)

        if forward != backward:
            return min(forward,backward)

        print(forward)
        print(backward)
        
        return forward

3차 시도

처음에 끝까지 curr 를 늘리면서 갔다가

stack 에 “(” 가 쌓여있는지 확인해서

몇번째 인덱스부터 문제였는지 다시 역탐색 하는 방법으로 구현

→ 쭉 갔다가 다시 stack 있는것 만큼 ← 되돌아가기

class Solution:
    def longestValidParentheses(self, s: str) -> int:
        if not s:
            return 0
        bracket_with_index = list(enumerate(s))
        #[(0, '('), (1, '('), (2, ')')] -> (인덱스,"(") 형태

        stack = []
        curr = 0
        max_valid = 0

        for i in range(len(bracket_with_index)):
            if bracket_with_index[i][1] == ")":
                if stack:
                    if stack[-1][1] == "(":
                        stack.pop()
                        curr += 2
                    else:
                        if curr:
                            max_valid = max(max_valid,curr)
                            curr = 0
                else:
                    if curr:
                        max_valid = max(max_valid,curr)
                        curr = 0
            else:
                stack.append(bracket_with_index[i])
        
        #print(stack)

        if stack:
            problem_index = stack.pop()[0]
            sub_curr = len(s)-1-problem_index
            max_valid = max(max_valid,sub_curr)
            #print(curr,sub_curr)
            curr = curr - sub_curr
            #print(stack)
            while stack and curr > 0:
                temp_problem_index = problem_index
                problem_index = stack.pop()[0]
                sub_curr = temp_problem_index-1-problem_index
                max_valid = max(max_valid,sub_curr)
                curr = curr - sub_curr
        #print(curr)
        if curr:
            max_valid = max(max_valid,curr)

        return max_valid

[해설코드] → 코드 완전 짧고 간단하다…

class Solution:
    def longestValidParentheses(self, s):
        longest = 0
        stack = [-1]
        for i, p in enumerate(s):
            if p == "(":
                stack.append(i)
            elif len(stack) == 1:
                stack[0] = i
            else:
                stack.pop()
                longest = max(longest, i - stack[-1])
        return longest

배우게 된 점 [ 필수 X ]

선형탐색 O(n) 으로 풀어야한다는 점을 알지만,

히든케이스 찾기가 너무 어렵다…..

해설방식을 보고 느낀점은 내가 좀 너무 어렵게 빙빙 돌아간 것이 아닌가 하는 생각이 든다. 기본 베이스 방법에서 부터 시작해서 방법을 바꿔나갔다면 좀 더 쉽게 접근할 수 있지 않았을까 하고 생각해본다.

그리고 지금 계속 반복적으로 시간복잡도를 줄이기위해서 index 와 pairing 하는 방법들이 보이고있다. 때문에 enumerate 함수랑 친해져야한다.

질문 [ 필수 X ]

자유 형식

피드백 [ 코치 작성 ]

수고하셨습니다!