[노씨데브 킬링캠프] 2주차 - 문제풀이: ★Trapping Rain Water★

KissNode·2024년 1월 15일

노씨데브 킬링캠프

목록 보기

21/73

★Trapping Rain Water★

Trapping Rain Water - LeetCode

★다시풀어볼 문제★ (100점 바로 맞긴 했는데 O(2n) 으로 풀었음. 다음번엔 O(n) 으로 풀수 있는 투포인터로 풀어보기)

접근 방법 [필수 작성]

제한 조건 확인

n 은 가로 길이, height[i] 는 세로 길이
가로길이 최대 2*10^4
세로길이 최대 10^5
뭔가 숫자크기가 n^2 으로 풀지 말라고 얘기하는 것 같다.
O(n) 으로 푸는 방법에 대해 생각해야할 것 같다.

아이디어

Example 1 그림

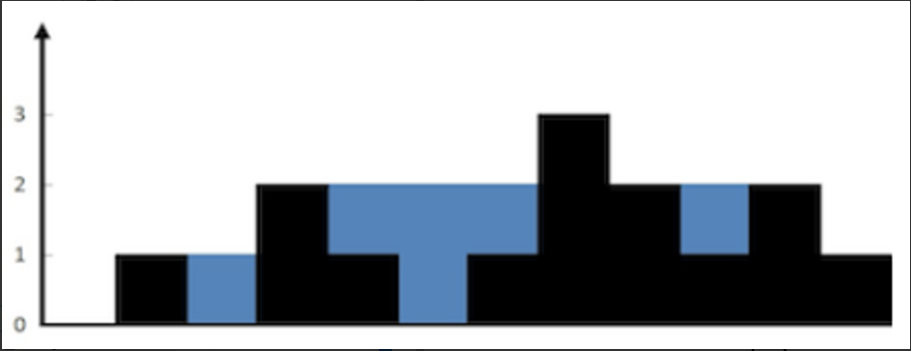
Example 2 그림

물이 채워지기 위한 조건?

특정 층에 물이 채워지려면 해당 높이와 동일한 기둥이 한개더 필요하다.

3층이상 기둥이 한개면 3층에는 물이 안채워진다.

2층이상 기둥이 3번째, 7번째, 8번째, 10번째면, 2층에는

7-3-1, 8-7-1, 10-8-1 만큼 물이 채워진다.

1층 이상 기둥이 1,3,4,6,7,8,9,10,11 번째에 있기 때문에

1층에 쌓이는 물은 3-1-1, 6-4-1 만큼 채워진다.

즉, 해당층수에서 다음칸 까지의 거리를 재서 더해주면 그게 총 물칸갯수이다.

그런데 위 방법으로 풀게되면

층수(10^5)만큼 칸수(2*10^4) 만큼 반복해야해서

2*10^9 이라 효율성 테스트에 통과하지 못할 것이다.

무조건 전체 칸수 한번 스윽 슬라이딩 했을때(O(n)) 문제 풀 수 있어야한다.

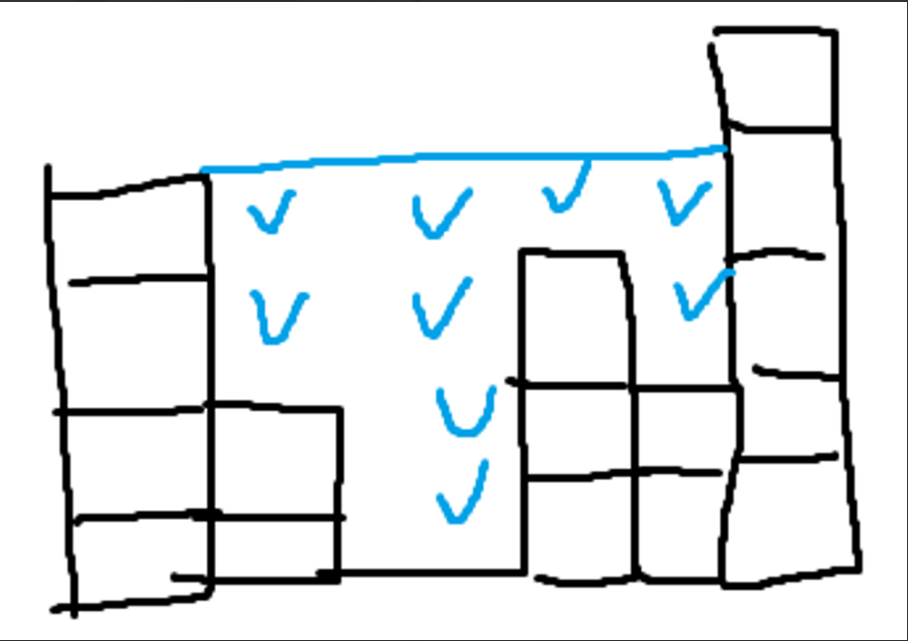
[위치index, 남은건물높이] → 형식으로 2중 리스트 작성

어떤 숫자들 사이에 0이 껴져있으면, 0갯수만큼 물칸 ++

0이 아닌 숫자들 다 - -

전체 다 0 될때까지 반복

[0,1,0,2,1,0,1,3,2,1,2,1] → 1+1

[0,0,0,1,0,0,0,2,1,0,1,0] → 3+1

[0,0,0,0,0,0,0,1,0,0,0,0] → 0

여기서 일일히 탐색해서는 안되고, 숫자가 있는 인덱스 위치를 활용하는 식으로 해야할 것 같음, enumerator 활용?

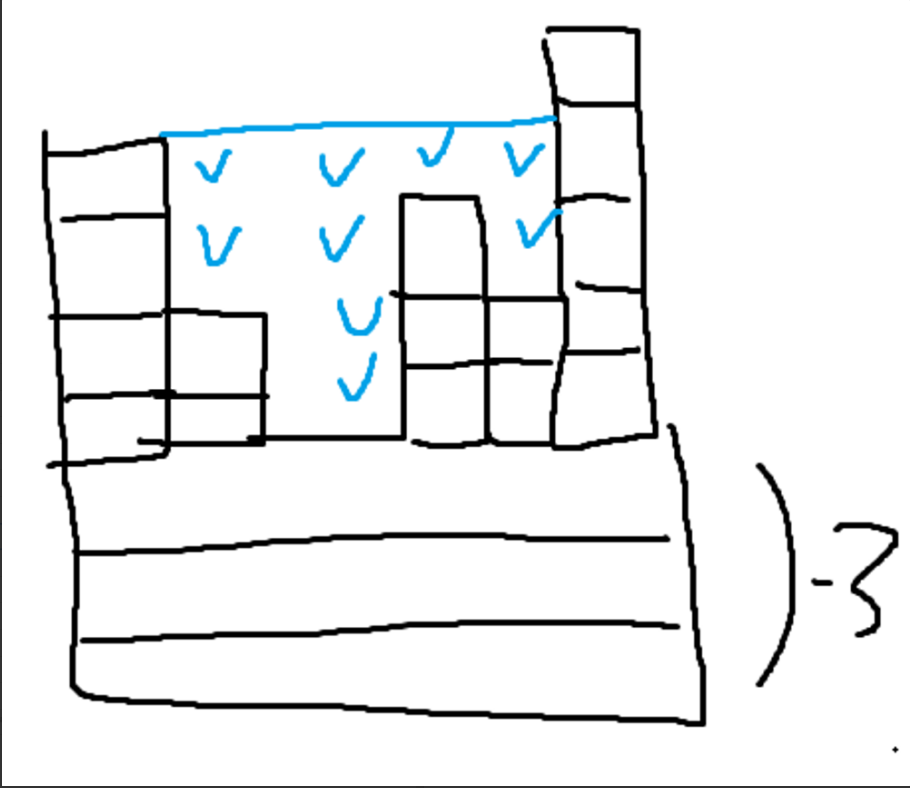
건물이 다같이 엄청 높을 때는 가장 작은 숫자만큼 확 빼버림

최종 아이디어 O(n) 으로 푸는법

curr = 현재까지의 물칸 저장값

max_h = 현재까지 나온 가장 높은 건물

[0,1,0,2,1,0,1,3,2,1,2,1]

칸 0번째부터 2*10^4 까지 탐색하는데

max_h 값에 현재 인덱스의 h 값을 빼서 curr에 누적합 해준다.

만약 탐색중에 현재 max_h 와 같거나 더 높은 값이 나오면

현재까지의 curr 값을 result 에 저장해주고, 계속 이어서 탐색한다.

끝까지 탐색후에 curr 에 남은 값이 있으면 ( 중간에 가장 높은 건물이 있다는 소리 )

거꾸로해서 똑같이 한번더 해준다.

시간복잡도

2210^4 = O(n)

자료구조

코드 구현 [필수 작성]

첫번째 시도

예시테케 다 맞아서 submit 했는데 만점 못받아서 코너 케이스 안보고 다시 생각시작 → 생각 도저히 안나서 테케 참고

반례:

[5,5,1,7,1,1,5,2,7,6]

같은 높이의 경우 2번 적용되는 문제가 있었음

if height[j] >= max_h:
>> 아래와 같이 수정
if height[j] > max_h:

# 6시 40분 시작 -> 
class Solution:
    def trap(self, height: List[int]) -> int:
        curr = 0
        max_h = 0
        answer = 0

        for i in range(len(height)):
            if height[i] >= max_h:
                answer += curr
                curr = 0
                max_h = height[i]
            curr += max_h - height[i]

        max_h = 0
        
        if curr != 0:
            curr = 0
            for j in range(len(height)-1,-1,-1):
                if height[j] >= max_h:
                    answer += curr
                    curr = 0
                    max_h = height[j]
                curr += max_h - height[j]
        
        return answer

두번째 시도

# 6시 40분 시작 -> 
class Solution:
    def trap(self, height: List[int]) -> int:
        curr = 0
        max_h = 0
        answer = 0

        for i in range(len(height)):
            if height[i] >= max_h:
                answer += curr
                curr = 0
                max_h = height[i]
            curr += max_h - height[i]
        print(curr)

        max_h = 0
        
        if curr != 0:
            curr = 0
            for j in range(len(height)-1,-1,-1):
                if height[j] > max_h:
                    answer += curr
                    curr = 0
                    max_h = height[j]
                curr += max_h - height[j]
        
        return answer