♠미로 탈출 명령어♠

♠열심히 연구했던 문제♠ (코드 최적화를 극한으로 해냈음)

접근 방법 [필수 작성]

문제이해

S->E 로 이동해야하는데 딱 K 번만큼가서 이동할수있는 경우가 있는지
있다면, 사전 오름차순상 가장 앞에 있는 것을 출력해야함 (d l r u) -> 가능하면 이 순서대로 가야함
없다면, impossible

제한 조건 확인

최대 50x50
k는 최대 2500
상하좌우 4방향
같은칸 반복가능

아이디어

같은칸 반복가능이어서 visited 의미없음
완탐하면 시간 안될수도
2500번인데, 한번할때 4방향임
그래서 인덱스 연산을 통한 카운팅으로 풀어야할것같음

정리하면,
S_r,S_c 와 E_r,E_c 가 있으면
E_r - S_r 가 양수면 그 절대값만큼 d 를 해주어야하고, 음수면 u 을 해줘야하고,
E_c - S_c 가 양수면 그 절대값만큼 r 를 해주어야하고, 음수면 l 을 해줘야한다.

그래서 각각이 필요한 갯수를 구하고, 불필요한 제자리연산을 추가해주면된다.
각각이 필요한 갯수는 우선 (d l r u) 순으로 배치한다. >>> ㄱ
그런데, 제자리연산은 반드시 짝수번만큼 필요하므로,
위 각각이 필요한 갯수를 총 더했을때, 음수거나 양수이면, K 또한 음수 또한 양수여야한다.
만약 그렇지 않다면, impossible 하다.
그리고 제자리연산을 추가할때 가능한 (d l r u) 이 순서로 해주어야하는데,
이때, 범위를 벗어나면 안된다.

범위벗어나는걸 어떻게 체크할거냐는 아이디어가 있어야한다.
총 4개의 리스트가 순서대로 있다.
d리스트, l리스트, r리스트, u리스트
ㄱ에서는 반드시 d랑u는 동시에 존재할수없고, l과r도 동시에 존재할 수 없다.

k가 0이 될때까지
현재 인덱스에서 d를 추가할 수 있다면,
범위가 나가지 않는만큼 d 리스트에 d를 추가하고 k를 하나씩 뺀다
d를 추가한 만큼 u리스트에 u를 추가하고 k를 하나씩 뺀다.
더이상 d를 추가할 수 없다면,
현재 인덱스에서 l를 추가할 수 있다면,
범위가 나가지 않는만큼 l를 추가하고 k를 하나씩 뺀다.
l를 추가한 만큼 r리스트에 r를 추가하고 k를 하나씩 뺀다.
l를 추가할수 없다면,
r리스트에 맨앞에rl를 하나씩 추가하고 k르 2개씩 뺀다.

현재까지 저장된 4개의 리스트를 순서대로 이어붙인다.

시간복잡도

선형 시간복잡도 여서 충분할것으로 예상

자료구조

코드 구현 [필수 작성]

1차 시도 (45분소요)

대부분의 테케 실패

로직의 문제가 있는듯

반례

3, 3, 1, 1, 3, 3, 8

기댓값 ddrlrlrr

결과값 ddllrrrr

도착지점을 기준으로만 생각할 것이 아니라, 현재 실시간 위치를 기준으로 생각해야함.

그런데 실시간 위치를 기준으로 생각할시, 남은k와 도착지까지의 거리를 미리 알 수 없기 때문에 그리디 로직으로는 갈 수가 없음

그렇다면, 도착지점을 기준으로 미리 제자리 연산 값들을 구해놓은 후 다시 처음지점을 기준으로 이동값들을 그리디하게 배치한다면 가능하지 않을까?

from collections import deque

def solution(n, m, x, y, r, c, k):
    answer = ''
    d_list = []
    l_list = []
    r_list = deque([])
    u_list = []
    tmp_k = k
    
    # S_r,S_ 와 E_r,E_c 가 있으면
    # E_r - S_r 가 양수면 그 절대값만큼 d 를 해주어야하고, 음수면 u 을 해줘야하고,
    # E_c - S_c 가 양수면 그 절대값만큼 r 를 해주어야하고, 음수면 l 을 해줘야한다.
    if r-x > 0:
        for _ in range(r-x):
            d_list.append("d")
            tmp_k -= 1
    else:
        for _ in range(abs(r-x)):
            u_list.append("u")
            tmp_k -= 1
    if c-y > 0:
        for _ in range(c-y):
            r_list.append("r")
            tmp_k -= 1
    else:
        for _ in range(abs(c-y)):
            l_list.append("l")
            tmp_k -= 1
            
    #print(d_list,l_list,r_list,u_list,tmp_k)
    
    # 그래서 각각이 필요한 갯수를 구하고, 불필요한 제자리연산을 추가해주면된다.
    # 각각이 필요한 갯수는 우선 (d l r u) 순으로 배치한다. >>> ㄱ
    # 그런데, 제자리연산은 반드시 짝수번만큼 필요하므로,
    # 위 각각이 필요한 갯수를 총 더했을때, 음수거나 양수이면, K 또한 음수 또한 양수여야한다.
    # 만약 그렇지 않다면, impossible 하다.
    
    if tmp_k % 2 == 1:
        return "impossible"
    
    
    # 그리고 제자리연산을 추가할때 가능한 (d l r u) 이 순서로 해주어야하는데,
    # 이때, 범위를 벗어나면 안된다.

    # 범위벗어나는걸 어떻게 체크할거냐는 아이디어가 있어야한다.
    # 총 4개의 리스트가 순서대로 있다.
    # d리스트, l리스트, r리스트, u리스트
    # ㄱ에서는 반드시 d랑u는 동시에 존재할수없고, l과r도 동시에 존재할 수 없다.

    # k가 0이 될때까지
    #     현재 인덱스에서 d를 추가할 수 있다면,
    #         범위가 나가지 않는만큼 d 리스트에 d를 추가하고 k를 하나씩 뺀다
    #         d를 추가한 만큼 u리스트에 u를 추가하고 k를 하나씩 뺀다.
    #     더이상 d를 추가할 수 없다면,
    #         현재 인덱스에서 l를 추가할 수 있다면,
    #             범위가 나가지 않는만큼 l를 추가하고 k를 하나씩 뺀다.
    #             l를 추가한 만큼 r리스트에 r를 추가하고 k를 하나씩 뺀다.
    #         l를 추가할수 없다면,
    #             r리스트에 맨앞에rl를 하나씩 추가하고 k를 2개씩 뺀다.
    while tmp_k > 0: #if 1 <= r <= n and 1 <= c <= m:
        if n-r > 0:
            d_list.append("d")
            tmp_k -= 1
            c += 1
            u_list.append("u")
            tmp_k -= 1
        elif c-1 > 0:
            l_list.append("l")
            tmp_k -= 1
            r -= 1
            r_list.append("r")
            tmp_k -= 1
        else:
            r_list.appendleft("rl")
            tmp_k -= 2
            
    # 현재까지 저장된 4개의 리스트를 순서대로 이어붙인다.
    answer += ''.join(d_list)
    answer += ''.join(l_list)
    answer += ''.join(r_list)
    answer +=''.join(u_list)
    
    return answer

2차 시도 (15분 소요)

들어가야할 글자들을 다 구해놓고 그리디하게 오름차순으로 배치한다는 로직으로 바꾸었지만 점수 조금 향상되었으나, 여전히 실패

반례

입력값 〉	3, 3, 3, 3, 1, 1, 8
기댓값 〉	"llrlrluu"
실행 결과 〉	실행한 결괏값 "llududuu"이 기댓값 "llrlrluu"과 다릅니다.

위 반례 또한, 도착지점을 기준으로 필요한 위치변경 연산들을 추가해주었기 때문임.

따라서, 뭔가 로직자체를 실시간 위치를 기반으로 할 수 있는 로직으로 변경해야함.

k-필수이동수 가 0 보다 큰 동안

d

우선 가지고 있는 d 다 소진

k 기준 제자리짓 해도되는지 확인

현재 위치에서 d 제자리짓할수있는지 확인

할수 있으면, k가 허용하는 연료 내 and 범위 내 에서 최대한 d 하고 u 나중에 할 거 기억추가

핵심은 남은 k번 만큼 제자리 operation 을 언제 얼마나 해줄지의 문제임.

최종도착하는데 쓸 연료만큼 남겨두고 내가 도중에 얼만큼 제자리짓을 하고 가도되는지 알 수 있어야함.

지속적으로 현재 k랑 어차피 필요할 연료량을 비교해봐야함

순서대로 dlru 리스트에서 꺼내쓰는데,

지속적으로 도착지까지 갈 연료 충분한지 파악

우선 있는 d 다쓰고, d 다 썼는데, 연료 아직 충분하면 내 범위 안에서 d 할수있는지 확인

할수 있으면, 할수 있는만큼 d하고, 나중에 u할거 기억해서 추가

'''
문제이해
S->E 로 이동해야하는데 딱 K 번만큼가서 이동할수있는 경우가 있는지
있다면, 사전 오름차순상 가장 앞에 있는 것을 출력해야함 (d l r u) -> 가능하면 이 순서대로 가야함
없다면, impossible 

제한조건
최대 50x50
k는 최대 2500
상하좌우 4방향
같은칸 반복가능

아이디어
같은칸 반복가능이어서 visited 의미없음
완탐하면 시간 안될수도
2500번인데, 한번할때 4방향임
그래서 인덱스 연산을 통한 카운팅으로 풀어야할것같음

정리하면,
S_r,S_c 와 E_r,E_c 가 있으면
E_r - S_r 가 양수면 그 절대값만큼 d 를 해주어야하고, 음수면 u 을 해줘야하고,
E_c - S_c 가 양수면 그 절대값만큼 r 를 해주어야하고, 음수면 l 을 해줘야한다.

그래서 각각이 필요한 갯수를 구하고, 불필요한 제자리연산을 추가해주면된다.
각각이 필요한 갯수는 우선 (d l r u) 순으로 배치한다. >>> ㄱ
그런데, 제자리연산은 반드시 짝수번만큼 필요하므로,
위 각각이 필요한 갯수를 총 더했을때, 음수거나 양수이면, K 또한 음수 또한 양수여야한다.
만약 그렇지 않다면, impossible 하다.
그리고 제자리연산을 추가할때 가능한 (d l r u) 이 순서로 해주어야하는데,
이때, 범위를 벗어나면 안된다.

범위벗어나는걸 어떻게 체크할거냐는 아이디어가 있어야한다.
총 4개의 리스트가 순서대로 있다.
d리스트, l리스트, r리스트, u리스트
ㄱ에서는 반드시 d랑u는 동시에 존재할수없고, l과r도 동시에 존재할 수 없다.

k가 0이 될때까지
    현재 인덱스에서 d를 추가할 수 있다면,
        범위가 나가지 않는만큼 d 리스트에 d를 추가하고 k를 하나씩 뺀다
        d를 추가한 만큼 u리스트에 u를 추가하고 k를 하나씩 뺀다.
    더이상 d를 추가할 수 없다면,
        현재 인덱스에서 l를 추가할 수 있다면,
            범위가 나가지 않는만큼 l를 추가하고 k를 하나씩 뺀다.
            l를 추가한 만큼 r리스트에 r를 추가하고 k를 하나씩 뺀다.
        l를 추가할수 없다면,
            r리스트에 맨앞에rl를 하나씩 추가하고 k르 2개씩 뺀다.

현재까지 저장된 4개의 리스트를 순서대로 이어붙인다.

시간복잡도

선형 시간복잡도 여서 충분할것으로 예상
'''
from collections import deque

def solution(n, m, x, y, r, c, k):
    answer = ''
    d_list = deque([])
    l_list = deque([])
    r_list = deque([])
    u_list = deque([])
    tmp_k = k
    
    # S_r,S_c 와 E_r,E_c 가 있으면
    # E_r - S_r 가 양수면 그 절대값만큼 d 를 해주어야하고, 음수면 u 을 해줘야하고,
    # E_c - S_c 가 양수면 그 절대값만큼 r 를 해주어야하고, 음수면 l 을 해줘야한다.
    if r-x > 0:
        for _ in range(r-x):
            d_list.append("d")
            tmp_k -= 1
    else:
        for _ in range(abs(r-x)):
            u_list.append("u")
            tmp_k -= 1
    if c-y > 0:
        for _ in range(c-y):
            r_list.append("r")
            tmp_k -= 1
    else:
        for _ in range(abs(c-y)):
            l_list.append("l")
            tmp_k -= 1
    
    # 그래서 각각이 필요한 갯수를 구하고, 불필요한 제자리연산을 추가해주면된다.
    # 각각이 필요한 갯수는 우선 (d l r u) 순으로 배치한다. >>> ㄱ
    # 그런데, 제자리연산은 반드시 짝수번만큼 필요하므로,
    # 위 각각이 필요한 갯수를 총 더했을때, 음수거나 양수이면, K 또한 음수 또한 양수여야한다.
    # 만약 그렇지 않다면, impossible 하다.
    
    if tmp_k % 2 == 1 or tmp_k < 0:
        return "impossible"
    
    
    
    # 그리고 제자리연산을 추가할때 가능한 (d l r u) 이 순서로 해주어야하는데,
    # 이때, 범위를 벗어나면 안된다.

    # 범위벗어나는걸 어떻게 체크할거냐는 아이디어가 있어야한다.
    # 총 4개의 리스트가 순서대로 있다.
    # d리스트, l리스트, r리스트, u리스트
    # ㄱ에서는 반드시 d랑u는 동시에 존재할수없고, l과r도 동시에 존재할 수 없다.

    # k가 0이 될때까지
    #     현재 인덱스에서 d를 추가할 수 있다면,
    #         범위가 나가지 않는만큼 d 리스트에 d를 추가하고 k를 하나씩 뺀다
    #         d를 추가한 만큼 u리스트에 u를 추가하고 k를 하나씩 뺀다.
    #     더이상 d를 추가할 수 없다면,
    #         현재 인덱스에서 l를 추가할 수 있다면,
    #             범위가 나가지 않는만큼 l를 추가하고 k를 하나씩 뺀다.
    #             l를 추가한 만큼 r리스트에 r를 추가하고 k를 하나씩 뺀다.
    #         l를 추가할수 없다면,
    #             r리스트에 맨앞에rl를 하나씩 추가하고 k를 2개씩 뺀다.
    tmp_r = r
    tmp_c = c
    
    while tmp_k > 0: #if 1 <= r <= n and 1 <= c <= m:
        if n-r > 0:
            d_list.append("d")
            tmp_k -= 1
            tmp_r += 1
            u_list.append("u")
            tmp_k -= 1
        elif c-1 > 0:
            l_list.append("l")
            tmp_k -= 1
            tmp_c -= 1
            r_list.append("r")
            tmp_k -= 1
        else:
            r_list.appendleft("rl")
            tmp_k -= 2
            
    # 현재까지 저장된 4개의 리스트를 실시간 위치값을 업데이트하면서 그리디하게 이어붙인다.
    # k만큼 도는데,
    # 현재 위치에서 아래로 갈 수 있으면 answer 에 d 추가하고 다음 루프
    # 현재 위치에서 아래로 못갈때, 왼쪽으로 갈 수 있으면 answer에 l 추가하고 다음 루프
    # 현재 위치에서 아래나 왼쪽으로 못가면, answer 에 r 추가하고 다음 루프
    # 현재위치에서 아래 왼 오 다 못가면 answer 에 u 추가하고 다음 루프
    
    #print(d_list,l_list,r_list,u_list,k)
    #print(n,r,c)
    
    for i in range(k):
        if n-x > 0 and d_list:
            answer += d_list.popleft()
            x += 1
        elif y-1 > 0 and l_list:
            answer += l_list.popleft()
            y -= 1
        elif r_list:
            r_or_rl = r_list.popleft()
            if r_or_rl == "r":
                answer += r_or_rl
                y += 1
            elif r_or_rl == "rl":
                answer += r_or_rl
        elif u_list:
            answer += u_list.popleft()
            x -= 1

    return answer

3차 시도 (40분 소요) (총 1시간40분소요)

풀긴 풀었는데 제출하기전까지도 while 문이 무한루프를 돌지 안돌지에 대한 확신이 없었다. 마지막의 else break 하는 구문이 뭔가 좀 찝찝하다.

        else:
            break

코드를 어떻게 개선할 수는 없을까?

'''
문제이해
S->E 로 이동해야하는데 딱 K 번만큼가서 이동할수있는 경우가 있는지
있다면, 사전 오름차순상 가장 앞에 있는 것을 출력해야함 (d l r u) -> 가능하면 이 순서대로 가야함
없다면, impossible 

제한조건
최대 50x50
k는 최대 2500
상하좌우 4방향
같은칸 반복가능

아이디어
같은칸 반복가능이어서 visited 의미없음
완탐하면 시간 안될수도
2500번인데, 한번할때 4방향임
그래서 인덱스 연산을 통한 카운팅으로 풀어야할것같음

정리하면,
S_r,S_c 와 E_r,E_c 가 있으면
E_r - S_r 가 양수면 그 절대값만큼 d 를 해주어야하고, 음수면 u 을 해줘야하고,
E_c - S_c 가 양수면 그 절대값만큼 r 를 해주어야하고, 음수면 l 을 해줘야한다.

그래서 각각이 필요한 갯수를 구하고, 불필요한 제자리연산을 추가해주면된다.
각각이 필요한 갯수는 우선 (d l r u) 순으로 배치한다. >>> ㄱ
그런데, 제자리연산은 반드시 짝수번만큼 필요하므로,
위 각각이 필요한 갯수를 총 더했을때, 음수거나 양수이면, K 또한 음수 또한 양수여야한다.
만약 그렇지 않다면, impossible 하다.
그리고 제자리연산을 추가할때 가능한 (d l r u) 이 순서로 해주어야하는데,
이때, 범위를 벗어나면 안된다.

범위벗어나는걸 어떻게 체크할거냐는 아이디어가 있어야한다.
총 4개의 리스트가 순서대로 있다.
d리스트, l리스트, r리스트, u리스트
ㄱ에서는 반드시 d랑u는 동시에 존재할수없고, l과r도 동시에 존재할 수 없다.

k가 0이 될때까지
    현재 인덱스에서 d를 추가할 수 있다면,
        범위가 나가지 않는만큼 d 리스트에 d를 추가하고 k를 하나씩 뺀다
        d를 추가한 만큼 u리스트에 u를 추가하고 k를 하나씩 뺀다.
    더이상 d를 추가할 수 없다면,
        현재 인덱스에서 l를 추가할 수 있다면,
            범위가 나가지 않는만큼 l를 추가하고 k를 하나씩 뺀다.
            l를 추가한 만큼 r리스트에 r를 추가하고 k를 하나씩 뺀다.
        l를 추가할수 없다면,
            r리스트에 맨앞에rl를 하나씩 추가하고 k르 2개씩 뺀다.

현재까지 저장된 4개의 리스트를 순서대로 이어붙인다.

시간복잡도

선형 시간복잡도 여서 충분할것으로 예상
'''
from collections import deque

def solution(n, m, x, y, r, c, k):
    answer = ''
    d_list = deque([])
    l_list = deque([])
    r_list = deque([])
    u_list = deque([])
    tmp_k = k
    
    # S_r,S_c 와 E_r,E_c 가 있으면
    # E_r - S_r 가 양수면 그 절대값만큼 d 를 해주어야하고, 음수면 u 을 해줘야하고,
    # E_c - S_c 가 양수면 그 절대값만큼 r 를 해주어야하고, 음수면 l 을 해줘야한다.
    if r-x > 0:
        for _ in range(r-x):
            d_list.append("d")
            tmp_k -= 1
    else:
        for _ in range(abs(r-x)):
            u_list.append("u")
            tmp_k -= 1
    if c-y > 0:
        for _ in range(c-y):
            r_list.append("r")
            tmp_k -= 1
    else:
        for _ in range(abs(c-y)):
            l_list.append("l")
            tmp_k -= 1
    
    # 그래서 각각이 필요한 갯수를 구하고, 불필요한 제자리연산을 추가해주면된다.
    # 각각이 필요한 갯수는 우선 (d l r u) 순으로 배치한다. >>> ㄱ
    # 그런데, 제자리연산은 반드시 짝수번만큼 필요하므로,
    # 위 각각이 필요한 갯수를 총 더했을때, 음수거나 양수이면, K 또한 음수 또한 양수여야한다.
    # 만약 그렇지 않다면, impossible 하다.
    
    if tmp_k % 2 == 1 or tmp_k < 0:
        return "impossible"
    
    
    
    # 그리고 제자리연산을 추가할때 가능한 (d l r u) 이 순서로 해주어야하는데,
    # 이때, 범위를 벗어나면 안된다.

    # 범위벗어나는걸 어떻게 체크할거냐는 아이디어가 있어야한다.
    # 총 4개의 리스트가 순서대로 있다.
    # d리스트, l리스트, r리스트, u리스트
    # ㄱ에서는 반드시 d랑u는 동시에 존재할수없고, l과r도 동시에 존재할 수 없다.

    # k가 0이 될때까지
    #     현재 인덱스에서 d를 추가할 수 있다면,
    #         범위가 나가지 않는만큼 d 리스트에 d를 추가하고 k를 하나씩 뺀다
    #         d를 추가한 만큼 u리스트에 u를 추가하고 k를 하나씩 뺀다.
    #     더이상 d를 추가할 수 없다면,
    #         현재 인덱스에서 l를 추가할 수 있다면,
    #             범위가 나가지 않는만큼 l를 추가하고 k를 하나씩 뺀다.
    #             l를 추가한 만큼 r리스트에 r를 추가하고 k를 하나씩 뺀다.
    #         l를 추가할수 없다면,
    #             r리스트에 맨앞에rl를 하나씩 추가하고 k를 2개씩 뺀다.
    
    # 여기까지 도착하는데 필요한 필수 연산들을 다 구했음
    # 필수연산들 cost 합 구하기
    est_cost = len(d_list) + len(l_list) + len(r_list) + len(u_list) #est meas essential, 필수 코스트
    
    def is_valid(nx,ny):
        if 1 <= nx <= n and 1 <= ny <= m:
            return True
        return False
    
    #print(d_list,l_list,r_list,u_list,k - est_cost)
        
    while k - est_cost >= 0:
        #print(answer,d_list,l_list,r_list,u_list,k - est_cost)
        while d_list:
            answer += d_list.popleft()
            x += 1
        if k - est_cost > 0:
            if is_valid(x + 1,y):
                d_list.append("d")
                u_list.append("u")
                k -= 2
                continue
        while l_list:
            answer += l_list.popleft()
            y -= 1
        if k - est_cost > 0:
            if is_valid(x,y - 1):
                l_list.append("l")
                r_list.append("r")
                k -= 2
                continue
        if k - est_cost > 0:
            answer += "rl"
            k -= 2
            continue
        if r_list:
            answer += r_list.popleft()
            y += 1
        elif u_list:
            answer += u_list.popleft()
            x -= 1
        else:
            break
    
    #print(d_list,l_list,r_list,u_list)

    return answer

배우게 된 점 [ 필수 X ]

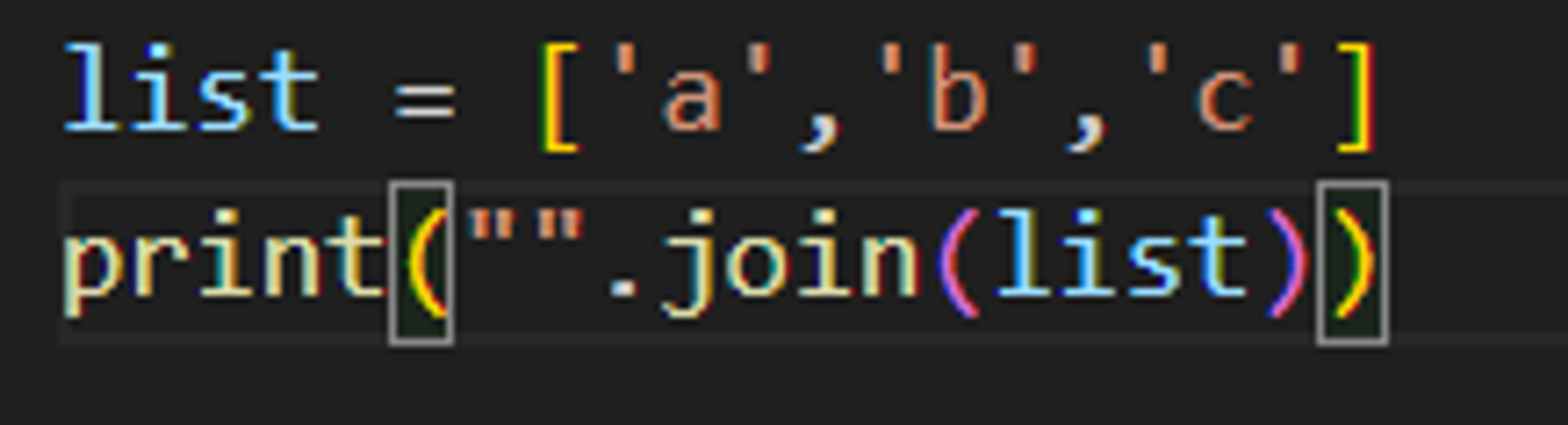
list 를 스트링으로 만들면, abc가 만들어지는게 아니고, 아예 리스트 통째로 스트링 형식으로 출력된다.

abc 로 출력하고 싶으면 join 을 활용하면 된다.

질문 [ 필수 X ]

Q1 스터디중 생겼던 코드비교로 인한 고민

지은님의 코드

import sys
sys.setrecursionlimit(10**8)

def solution(n, m, x, y, r, c, k):

    # 사전 순으로 출발하도록
    directions = ['d', 'l', 'r', 'u']
    dx = [1, 0, 0, -1]
    dy = [0, -1, 1, 0]
    answer = 'z'

    def dfs(cy, cx, path, cnt):
        nonlocal answer

				#print(path) -> 1번 위치

        # 현재 거리가 목표 지점에서 멀어진 경우
        if cnt + abs(cy-c) + abs(cx-r) > k:
            return

        # k 보다 더 많이 이동한 경우
        if cnt > k:
            return

        if cnt == k:
            if cx == r and cy == c:
                answer = path
                return answer

				#print(path) -> 2번 위치

        for i in range(4):
            ny = cy + dy[i]
            nx = cx + dx[i]
            if 1 <= ny <= m and 1 <= nx <= n:
                if path < answer:
                    if dfs(ny, nx, path + directions[i], cnt + 1):
                        return answer

    # 탈출 불가능 조건
    # 1. k가 최단 거리보다 작은 경우
    # 2. 좌표에 도착할 수 있는 횟수는 최소 거리 + 2의 배수 씩 증가 ****** 31번 테스트케이스
    dist = abs(x - r) + abs(y - c)
    if dist > k or (k-dist) % 2 == 1:
        return 'impossible'

    dfs(y, x, "", 0)

    if answer == 'z':
        return 'impossible'

    return answer

처음생각

스터디에서 지은님 코드와 제 코드를 비교하던 중 이상한 점을 발견했습니다. 저는 처음에 문제를 접근할 때, 같은칸 반복가능이어서 visited 의미없음
완탐하면 시간 안될수도
2500번인데, 한번할때 4방향임
그래서 인덱스 연산을 통한 카운팅으로 풀어야할것같음 ← 이와 같은 이유로, bfs 나 dfs 로 불필요한 연산이 추가되면 시간초과가 날 것으로 예상했습니다. 하지만 다음의 지은님코드는 제가 우려했던 불필요한 연산이 발생하는데도 불구하고, 통과하였습니다. 해당 부분에 대해서 k가 매우커져 2500이 될 경우에는 불필요한 재귀발생때문에 적절한 히든 테스트케이스가 있다면 실패하는 코드라고 생각하는데 재귀의 시간복잡도를 계산하기 힘들어 제 생각이 맞는지 모르겠습니다.

지은님 코드 결과

입력값 〉	3, 3, 3, 1, 1, 3, 8
기댓값 〉	"rlrlrruu"
실행 결과 〉	테스트를 통과하였습니다.
출력 〉	r

rl
rlr
rlrl
rlrlr
rlrlrl → 불필요재귀발생
rlrlrr
rlrlrrl → 불필요재귀발생
rlrlrru
rlrlrrud → 불필요재귀발생
rlrlrrul → 불필요재귀발생
rlrlrruu |

제 코드 결과

입력값 〉	3, 3, 3, 1, 1, 3, 8
기댓값 〉	"rlrlrruu"
실행 결과 〉	테스트를 통과하였습니다.
출력 〉	rl

rlrl
rlrlr
rlrlrr
rlrlrru
rlrlrruu |

고민 후 다시 생각

지은님의 아래 해당 조건 코드는

if cnt + abs(cy-c) + abs(cx-r) > k:
            return

제 코드의 while문 조건 코드와 동일한 효과를 냅니다.

while k - est_cost >= 0:

지은님의 코드 또한 해당 조건을 통해 불표한 재귀가 실행되지 않고 바로 빠져나오는 효과를 가집니다.

해당 결과처럼 프린트된 이유는

[import sys
sys.setrecursionlimit(10**8)

def solution(n, m, x, y, r, c, k):

# 사전 순으로 출발하도록
directions = ['d', 'l', 'r', 'u']
dx = [1, 0, 0, -1]
dy = [0, -1, 1, 0]
answer = 'z'

def dfs(cy, cx, path, cnt):
    nonlocal answer

			#print(path) -> 1번 위치

    # 현재 거리가 목표 지점에서 멀어진 경우
    if cnt + abs(cy-c) + abs(cx-r) > k:
        return

    # k 보다 더 많이 이동한 경우
    if cnt > k:
        return

    if cnt == k:
        if cx == r and cy == c:
            answer = path
            return answer

			#print(path) -> 2번 위치

    for i in range(4):
        ny = cy + dy[i]
        nx = cx + dx[i]
        if 1 <= ny <= m and 1 <= nx <= n:
            if path < answer:
                if dfs(ny, nx, path + directions[i], cnt + 1):
                    return answer

# 탈출 불가능 조건
# 1. k가 최단 거리보다 작은 경우
# 2. 좌표에 도착할 수 있는 횟수는 최소 거리 + 2의 배수 씩 증가 ****** 31번 테스트케이스
dist = abs(x - r) + abs(y - c)
if dist > k or (k-dist) % 2 == 1:
    return 'impossible'

dfs(y, x, "", 0)

if answer == 'z':
    return 'impossible'

return answer](https://www.notion.so/import-sys-sys-setrecursionlimit-10-8-def-solution-n-m-x-y-r-c-k--93aa2c8e088e4d9e99f0094ab5bb9010?pvs=21) ← 지은님 코드에서 프린트문을 1번위치에 놓느냐, 2번위치에 놓느냐 차이로 보입니다. 즉, 지은님 코드 또한 제 코드와 동일하게 불필요한 연산이 발생하지 않고 완전히 동일한 그리디탐색을 진행하는 것으로 보입니다.

→ 제 생각이 맞는건지 궁금합니다.

Q2 (추가질문)

1. 또한 동연님의 코드의 경우 조금만 더 논리를 수정한다면 whlie문 없이도 한번에 필요한 d, l, rl, r, u의 개수를 찾아서 O(1)의 시간 내에 답을 구할 수 있습니다. → 이미 제 코드는 선형탐색시간내에 문제를 해결하고 있는거 아닌가요?

또, 코드 수정을 시도해보았지만, 아예 while문을 사용하지 않고 만드는게 가능한지 궁금합니다. 제가 생각하기에 한번에 필요한 d l rl r u 의 갯수를 업데이트할 수 없는 이유는 실시간 위치를 탐색해서 해당 실시간 위치에서 남은 k - est_cost 여분만큼 du 던, lr 이던, rl 이던 추가를 해주어야하기 때문에 리스트내 몇개의 원소가 있는지 특정할 수 없고, 또 추후에 몇개의 원소가 들어갈 수 있는지도 특정할 수 없기때문에, 리스트내원소를 최대한 다 뽑아내고 진행하려면 while문을 사용하지 않고 구현하려하니 어려운데 어떻게 while 문 사용없이 한번에 모든 필요연산을 다 구할 수 있나요?

[ While문 없이 구현하기 ]

1차시도

또 for문 iteration 에 영향을 주는 x를 for문 안에서 바꾸고 있어서 문제가 된 것임.

        for _ in range(n - x):
            if not is_valid(x + 1,y):
                break
            if k <= 0:
                break
            d_list.append("d")
            u_list.append("u")
            k -= 2
            x += 1 -> 또 for문 iteration 에 영향을 주는 x를 바꾸고 있음

from collections import deque

def solution(n, m, x, y, r, c, k):
    answer = ''
    d_list = deque([])
    l_list = deque([])
    r_list = deque([])
    u_list = deque([])
    tmp_k = k
    
    # S_r,S_c 와 E_r,E_c 가 있으면
    # E_r - S_r 가 양수면 그 절대값만큼 d 를 해주어야하고, 음수면 u 을 해줘야하고,
    # E_c - S_c 가 양수면 그 절대값만큼 r 를 해주어야하고, 음수면 l 을 해줘야한다.
    if r-x > 0:
        for _ in range(r-x):
            d_list.append("d")
            tmp_k -= 1
    else:
        for _ in range(abs(r-x)):
            u_list.append("u")
            tmp_k -= 1
    if c-y > 0:
        for _ in range(c-y):
            r_list.append("r")
            tmp_k -= 1
    else:
        for _ in range(abs(c-y)):
            l_list.append("l")
            tmp_k -= 1
    
    # 그래서 각각이 필요한 갯수를 구하고, 불필요한 제자리연산을 추가해주면된다.
    # 각각이 필요한 갯수는 우선 (d l r u) 순으로 배치한다. >>> ㄱ
    # 그런데, 제자리연산은 반드시 짝수번만큼 필요하므로,
    # 위 각각이 필요한 갯수를 총 더했을때, 음수거나 양수이면, K 또한 음수 또한 양수여야한다.
    # 만약 그렇지 않다면, impossible 하다.
    
    if tmp_k % 2 == 1 or tmp_k < 0:
        return "impossible"
    
    
    
    # 그리고 제자리연산을 추가할때 가능한 (d l r u) 이 순서로 해주어야하는데,
    # 이때, 범위를 벗어나면 안된다.

    # 범위벗어나는걸 어떻게 체크할거냐는 아이디어가 있어야한다.
    # 총 4개의 리스트가 순서대로 있다.
    # d리스트, l리스트, r리스트, u리스트
    # ㄱ에서는 반드시 d랑u는 동시에 존재할수없고, l과r도 동시에 존재할 수 없다.

    # k가 0이 될때까지
    #     현재 인덱스에서 d를 추가할 수 있다면,
    #         범위가 나가지 않는만큼 d 리스트에 d를 추가하고 k를 하나씩 뺀다
    #         d를 추가한 만큼 u리스트에 u를 추가하고 k를 하나씩 뺀다.
    #     더이상 d를 추가할 수 없다면,
    #         현재 인덱스에서 l를 추가할 수 있다면,
    #             범위가 나가지 않는만큼 l를 추가하고 k를 하나씩 뺀다.
    #             l를 추가한 만큼 r리스트에 r를 추가하고 k를 하나씩 뺀다.
    #         l를 추가할수 없다면,
    #             r리스트에 맨앞에rl를 하나씩 추가하고 k를 2개씩 뺀다.
    
    # 여기까지 도착하는데 필요한 필수 연산들을 다 구했음
    # 필수연산들 cost 합 구하기
    est_cost = len(d_list) + len(l_list) + len(r_list) + len(u_list) #est meas essential, 필수 코스트
    
    def is_valid(nx,ny):
        if 1 <= nx <= n and 1 <= ny <= m:
            return True
        return False
    
    #print(d_list,l_list,r_list,u_list,k - est_cost)
    k -= est_cost
    
    if k > 0:
        x += len(d_list)
        for _ in range(n - x):
            if not is_valid(x + 1,y):
                break
            if k <= 0:
                break
            d_list.append("d")
            u_list.append("u")
            k -= 2
            x += 1 -> 또 for문 iteration 에 영향을 주는 x를 바꾸고 있음
        y -= len(l_list)
        for _ in range(m - y):
            if not is_valid(x,y - 1):
                break
            if k <= 0:
                break
            l_list.append("l")
            r_list.append("r")
            k -= 2
            y -= 1 -> -> 또 for문 iteration 에 영향을 주는 y를 바꾸고 있음
        for _ in range(k // 2):
            r_list.appendleft("rl")
    
    answer = "".join(d_list) + "".join(l_list) + "".join(r_list) + "".join(u_list)

    return answer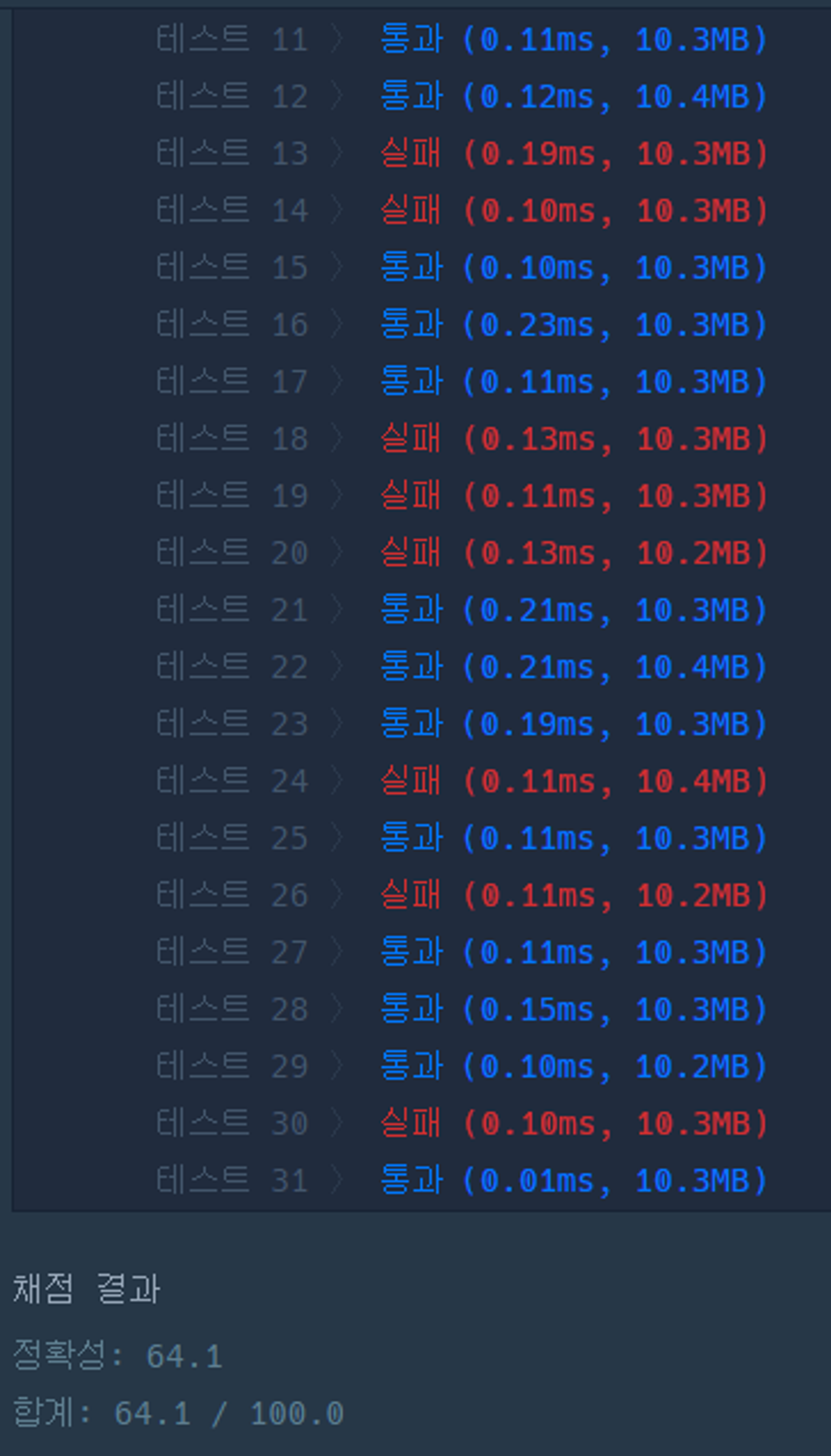

2차 시도

해당 부분 수정해주니 all 통과

하지만 여전히 최적화 할 수 있는 부분 남아있음

k를 반복문을 통해 2씩 빼는게 아닌 한번에 구할 수 있는 방법이 있음

from collections import deque

def solution(n, m, x, y, r, c, k):
    answer = ''
    d_list = deque([])
    l_list = deque([])
    r_list = deque([])
    u_list = deque([])
    tmp_k = k
    
    # S_r,S_c 와 E_r,E_c 가 있으면
    # E_r - S_r 가 양수면 그 절대값만큼 d 를 해주어야하고, 음수면 u 을 해줘야하고,
    # E_c - S_c 가 양수면 그 절대값만큼 r 를 해주어야하고, 음수면 l 을 해줘야한다.
    if r-x > 0:
        for _ in range(r-x):
            d_list.append("d")
            tmp_k -= 1
    else:
        for _ in range(abs(r-x)):
            u_list.append("u")
            tmp_k -= 1
    if c-y > 0:
        for _ in range(c-y):
            r_list.append("r")
            tmp_k -= 1
    else:
        for _ in range(abs(c-y)):
            l_list.append("l")
            tmp_k -= 1
    
    # 그래서 각각이 필요한 갯수를 구하고, 불필요한 제자리연산을 추가해주면된다.
    # 각각이 필요한 갯수는 우선 (d l r u) 순으로 배치한다. >>> ㄱ
    # 그런데, 제자리연산은 반드시 짝수번만큼 필요하므로,
    # 위 각각이 필요한 갯수를 총 더했을때, 음수거나 양수이면, K 또한 음수 또한 양수여야한다.
    # 만약 그렇지 않다면, impossible 하다.
    
    if tmp_k % 2 == 1 or tmp_k < 0:
        return "impossible"
    
    
    
    # 그리고 제자리연산을 추가할때 가능한 (d l r u) 이 순서로 해주어야하는데,
    # 이때, 범위를 벗어나면 안된다.

    # 범위벗어나는걸 어떻게 체크할거냐는 아이디어가 있어야한다.
    # 총 4개의 리스트가 순서대로 있다.
    # d리스트, l리스트, r리스트, u리스트
    # ㄱ에서는 반드시 d랑u는 동시에 존재할수없고, l과r도 동시에 존재할 수 없다.

    # k가 0이 될때까지
    #     현재 인덱스에서 d를 추가할 수 있다면,
    #         범위가 나가지 않는만큼 d 리스트에 d를 추가하고 k를 하나씩 뺀다
    #         d를 추가한 만큼 u리스트에 u를 추가하고 k를 하나씩 뺀다.
    #     더이상 d를 추가할 수 없다면,
    #         현재 인덱스에서 l를 추가할 수 있다면,
    #             범위가 나가지 않는만큼 l를 추가하고 k를 하나씩 뺀다.
    #             l를 추가한 만큼 r리스트에 r를 추가하고 k를 하나씩 뺀다.
    #         l를 추가할수 없다면,
    #             r리스트에 맨앞에rl를 하나씩 추가하고 k를 2개씩 뺀다.
    
    # 여기까지 도착하는데 필요한 필수 연산들을 다 구했음
    # 필수연산들 cost 합 구하기
    est_cost = len(d_list) + len(l_list) + len(r_list) + len(u_list) #est meas essential, 필수 코스트
    
    def is_valid(nx,ny):
        if 1 <= nx <= n and 1 <= ny <= m:
            return True
        return False
    
    #print(d_list,l_list,r_list,u_list,k - est_cost)
    k -= est_cost
    
    if k > 0:
        x += len(d_list)
        for _ in range(n - x):
            if k <= 0:
                break
            d_list.append("d")
            u_list.append("u")
            k -= 2
        y -= len(l_list)
        for _ in range(y-1):
            if k <= 0:
                break
            l_list.append("l")
            r_list.append("r")
            k -= 2
        for _ in range(k // 2):
            r_list.appendleft("rl")
    
    answer = "".join(d_list) + "".join(l_list) + "".join(r_list) + "".join(u_list)

    return answer

3차 시도

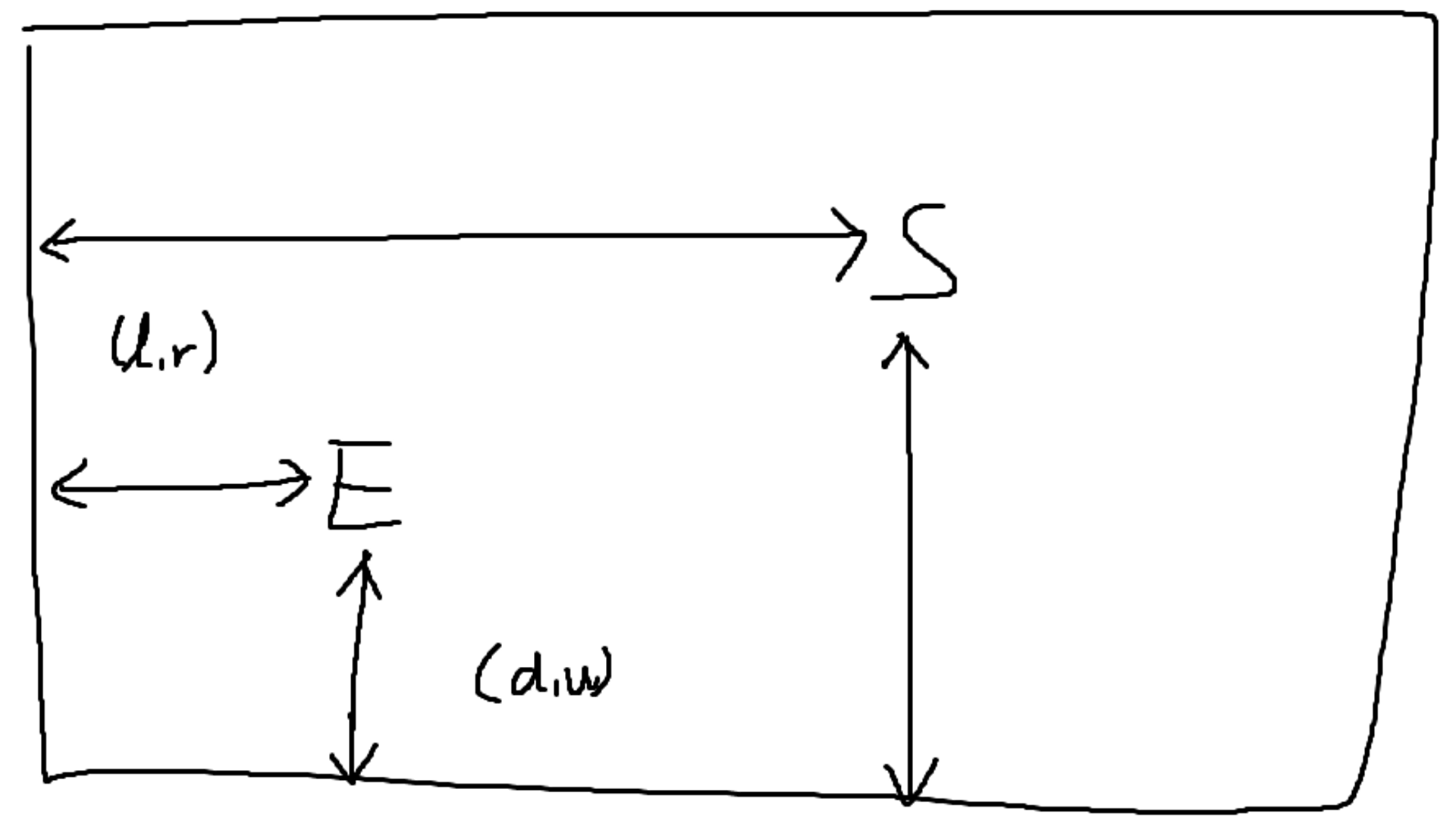
k를 반복문을 통해 2씩 빼는게 아닌 아예 d,u 세트가 몇개 들어갈지, l,r 세트가 몇개 들어갈지 통째로 구하고 시작할 수 있음.

k가 충분히 많을땐, S 와 E 중 row 값이 더 큰값을 기준 (아래로 갈 수 있는 여분값) x 2 만큼 (d,u) 세트를 추가할 수 있음. → ⓐ

그런 다음, 동일하게 S 와 E 중 col 값이 더 큰값을 기준 (왼쪽으로 갈 수 있는 여분값) x 2 만큼 (l,r) 세트를 추가할 수 있음. → ⓑ

남은 k 만큼 k // 2 만큼 rl 를 r_list 앞에 추가할 수 있음. ⓒ

만약 ⓐ,ⓑ 를 실행하는 도중 k 가 부족할 때는 ⓒ와 동일하게 해당 부분에서 k//2 만큼 해당 부분을 추가해주면 됨.

같은 선형시간복잡도 풀이의 코드이지만 연산량 자체를 최적의 최적으로 줄일 수 있음.

컴퓨팅 파워 사용의 최적화가 중요할때 이렇게까지 최적화 할 수 있다는 것을 보여줄 수 있는 예가 됨.

[ 최종코드 ]

from collections import deque

def solution(n, m, x, y, r, c, k):
    answer = ''
    d_list = deque([])
    l_list = deque([])
    r_list = deque([])
    u_list = deque([])
    tmp_k = k
    
    if r-x > 0:
        for _ in range(r-x):
            d_list.append("d")
            tmp_k -= 1
    else:
        for _ in range(abs(r-x)):
            u_list.append("u")
            tmp_k -= 1
    if c-y > 0:
        for _ in range(c-y):
            r_list.append("r")
            tmp_k -= 1
    else:
        for _ in range(abs(c-y)):
            l_list.append("l")
            tmp_k -= 1

    if tmp_k % 2 == 1 or tmp_k < 0:
        return "impossible"

    est_cost = len(d_list) + len(l_list) + len(r_list) + len(u_list) #est meas essential, 필수 코스트
    
    def is_valid(nx,ny):
        if 1 <= nx <= n and 1 <= ny <= m:
            return True
        return False
    
    k -= est_cost
    
    if r > x:
        possible_d = n - r
    else:
        possible_d = n - x
    
    if c < y:
        possible_l = c - 1
    else:
        possible_l = y - 1
    
#최적화된 부분
    if k > 0:
        if k - possible_d*2 >= 0:
            for _ in range(possible_d):
                d_list.append("d")
                u_list.append("u")
            k -= possible_d*2
        else:
            for _ in range(k // 2):
                d_list.append("d")
                u_list.append("u")
            k = 0
            
        if k - possible_l*2 >= 0:
            for _ in range(possible_l):
                l_list.append("l")
                r_list.append("r")
            k -= possible_l*2
        else:
            for _ in range(k // 2):
                l_list.append("l")
                r_list.append("r")
            k = 0
        if k > 0:
            for _ in range(k // 2):
                r_list.appendleft("rl")
    
    answer = "".join(d_list) + "".join(l_list) + "".join(r_list) + "".join(u_list)

    return answer

연산속도 비교 (최적화 코드)

연산속도 비교 (기존 코드)

대부분의 테스트케이스에서 유의미한 효율성향상을 보여줌.

피드백 [ 코치 작성 ]

A1

지은님의 코드와 동연님의 코드의 논리는 동일하지 않지만 둘 모두 상당수의 불필요한 연산을 배제하여 통과하게 됩니다. 동연님의 코드는 현재 상황에서 선택할 수 있는 최적을 이후의 상황까지 고려하여 선택하기에(d를 추가할 때 u도 같이 추가, l을 추가할 때 r도 같이 추가) 이후에 발생할 수 있는 모든 불필요한 가능성을 배제하지만 지은님의 코드의 경우 현재 상황에서 최적인 경우의 수만 선택할 뿐 이후에 발생하는 불필요한 가능성은 배제되지 않았습니다. 배제된 가능성은 목적지로부터 지나치게 멀어져 목적지에 도달할 수 없는 경우이며 이 조건만으로 상당수의 가능성이 배제되어 통과하게 된 것입니다.

또한 동연님의 코드의 경우 조금만 더 논리를 수정한다면 whlie문 없이도 한번에 필요한 d, l, rl, r, u의 개수를 찾아서 O(1)의 시간 내에 답을 구할 수 있습니다.

A2

1. 설명이 모호했던 것 같습니다. 동연님의 코드는 이미 O(1)의 시간복잡도를 갖고 있으며 제가 설명한 내용은 while문을 제거할 수 있다는 내용이였습니다.
2. while문을 제거할 수 있는 이유는 다음과 같습니다. 우선 초기 시작점부터 목적지까지 가는 데 걸리는 d, l, r, u의 횟수를 구하면 남은 횟수가 존재합니다. 이 때 목적지 까지 가는 데 걸리는 횟수들을 이미 구한 상태이기에 이미 목적지에 도착할 수 있는 상태입니다. 즉 남은 횟수들을 (d, u), (l, r)쌍으로 최대한 배제한 후 그 후에도 남은 횟수는 rl 명령어로 처리되게 됩니다. 즉 초기 dlru를 전부 구한 후 남은 횟수 ⇒ (d,u)쌍으로 최대한 배제 ⇒ 그 후에도 남은 횟수 ⇒ (l,r)쌍으로 최대한 배제 ⇒ 그 후에도 남은 횟수(이 때 현재 위치는 왼쪽 아래 구석(n,0)) ⇒ rl으로 처리