블록 이동하기

접근 방법 [필수 작성]

문제이해

0은 빈칸, 1은 벽
(1,1)부터 시작
회전하거나 이동할때 걸리는 벽이 없어야한다
(N,N) 도착지점까지 이동하는 최단 시간을 리턴 -> BFS 로 접근가능

제한 조건 확인

최대 100x100 보드
목적지에 도착할 수 있는 경우만 주어짐

아이디어

비슷하게 움직였다고 생각하더라도,
로봇이 도착지점에 먼저 닿는걸 기준으로 하기 때문에
축의 회전을 효율적으로 해야한다.

각 단계에서 로봇이 할 수 있는 모든 행위를 조사
동일한 케이스를 만나면 탐색하지 않음

각 스테이지의 로봇의 상태는 2개의 픽셀값으로 구분됨
두 픽셀중 어느하나라도 도착지점에 도착하면 끝

각 단계 로봇이 할 수 있느 행위는
왼쪽을 축으로 시계방향, 반시계방향
오른쪽을 축으로 시계방향, 반시계방향이 있을 수 있으며
회전의 경우
드론이 가로로 놓여있으면 드론기준 위와 아래를 체크하면되고
드론이 세로로 놓여있으면 드론기준 양 옆을 체크하면된다

위,아래,좌,우 행위가 있을 수 있으므로
총 8개의 행위가 가능하다

8개의 행위 중 회전방향에 1이 있거나 이동방향에 1이 있으면 다음 단계를 큐에 넣지 못한다.

시간복잡도

시간 충분할것으로 예상

자료구조

bfs 이기때문에 큐를 활용
큐안에는 두개의 픽셀값이 들어가는데, sort 되어서 들어감
visited 는 sort된 픽셀의 set 을 활용해 방문여부를 확인함

회전이 가능한지 조사하는 함수
이동이 가능한지 조사하는 함수
회전시키는 함수
이동시키는 함수
메인함수 -> 전체 큐 관리 및 도착 여부 확인

코드 구현 [필수 작성]

1차 시도 (1시간15분)

한방에 통과

회전 구현 생각이 처음에 어려웠음

반복되는 구조 가독성 높이기 및 최적화 하기

from collections import deque

def solution(board):
        
    answer = 0
    
    dr = [0,1,0,-1]
    dc = [1,0,-1,0]
    
    N = len(board)
    visited = set()
    q = deque([])
    q.append([[(0,0),(0,1)],0])  # 각 case 는 [[(a,b),(c,d)],count] 꼴
    
    def is_valid(r,c):
        if 0 <= r < N and 0 <= c < N and board[r][c] == 0:
            return True
        return False
    
    
    def add_np(p,cnt):
        nonlocal visited
        nonlocal q
        
        p.sort()
        if tuple(p) not in visited:
            visited.add(tuple(p))
            q.append([p,cnt+1])
        
    
    while q:
        tp,tmp_cnt = q.popleft()
        tp1,tp2 = tp
        #print(tp1,tp2,tmp_cnt)
        if (tp1[0] == N-1 and tp1[1] == N-1) or (tp2[0] == N-1 and tp2[1] == N-1):
            return tmp_cnt
        for i in range(4): #상하좌우
            np1_r = tp1[0] + dr[i]
            np1_c = tp1[1] + dc[i]
            np2_r = tp2[0] + dr[i]
            np2_c = tp2[1] + dc[i]
            if is_valid(np1_r,np1_c) and is_valid(np2_r,np2_c):
                np = [(np1_r,np1_c),(np2_r,np2_c)]
                add_np(np,tmp_cnt)
        #회전시에는 각 원소 어펜드하기전 sort해주고, sort한거 set 에 있는 지 확인후 없으면 append해야함
        if tp1[0] == tp2[0]: #드론이 가로로 놓인경우
            #위 방향을 확인 후 둘다 0이고 범위안이어서 가능하면,
            if is_valid(tp1[0]-1,tp1[1]) and is_valid(tp2[0]-1,tp2[1]):
                #왼쪽축기준 반시계방향 회전 가능
                np = [(tp1[0],tp1[1]),(tp2[0]-1,tp2[1]-1)]
                add_np(np,tmp_cnt)
                #오른쪽축기준 시계방향 회전 가능
                np = [(tp1[0]-1,tp1[1]+1),(tp2[0],tp2[1])]
                add_np(np,tmp_cnt)
            #아래 방향을 확인 후 둘다 0이고 범위안이어서 가능하면,
            if is_valid(tp1[0]+1,tp1[1]) and is_valid(tp2[0]+1,tp2[1]):
                #왼쪽축기준 시계방향
                np = [(tp1[0],tp1[1]),(tp2[0]+1,tp2[1]-1)]
                add_np(np,tmp_cnt)
                #오른쪽축기준 반시계방향 회전 가능
                np = [(tp1[0]+1,tp1[1]+1),(tp2[0],tp2[1])]
                add_np(np,tmp_cnt)
        elif tp1[1] == tp2[1]: #드론이 세로로 놓인경우
            #왼쪽 방향을 확인 후 둘다 0이고 범위안이어서 가능하면,
            if is_valid(tp1[0],tp1[1]-1) and is_valid(tp2[0],tp2[1]-1):
                #위쪽축기준 시계방향
                np = [(tp1[0],tp1[1]),(tp2[0]-1,tp2[1]-1)]
                add_np(np,tmp_cnt)
                #아래쪽축기준 반시계방향
                np = [(tp1[0]+1,tp1[1]-1),(tp2[0],tp2[1])]
                add_np(np,tmp_cnt)
            #오른쪽 방향을 확인 후 둘다 0이고 범위안이어서 가능하면,
            if is_valid(tp1[0],tp1[1]+1) and is_valid(tp2[0],tp2[1]+1):
                #위쪽축기준 반시계방향
                np = [(tp1[0],tp1[1]),(tp2[0]-1,tp2[1]+1)]
                add_np(np,tmp_cnt)
                #아래쪽축기준 시계방향
                np = [(tp1[0]+1,tp1[1]+1),(tp2[0],tp2[1])]
                add_np(np,tmp_cnt)

2차 시도(가독성 및 코드최적화)

회전하는 부분(아래 코드 중 #회전파트)에서 반복되는 부분이 생기기는 하는데

세로일때와 가로일때 처리해주어야하는 픽셀기준이 달라서

함수로 빼기가 힘든것같다.

어떻게 리팩토링하여 가독성을 높힐 수 있을지 잘 모르겠다.

from collections import deque

def solution(board):
        
    answer = 0
    
    dr = [0,1,0,-1]
    dc = [1,0,-1,0]
    
    N = len(board)
    visited = set()
    q = deque([])
    q.append([[(0,0),(0,1)],0])
    
    def is_valid(r,c):
        if 0 <= r < N and 0 <= c < N and board[r][c] == 0:
            return True
        return False
    
    def add_np(p,cnt):
        nonlocal visited
        nonlocal q
        
        p.sort()
        if tuple(p) not in visited:
            visited.add(tuple(p))
            q.append([p,cnt+1])
        
    
    while q:
        tp,tmp_cnt = q.popleft()
        tp1,tp2 = tp
        if tp1 == (N-1,N-1) or tp2 == (N-1,N-1):
            return tmp_cnt
        for i in range(4):
            np1_r = tp1[0] + dr[i]
            np1_c = tp1[1] + dc[i]
            np2_r = tp2[0] + dr[i]
            np2_c = tp2[1] + dc[i]
            if is_valid(np1_r,np1_c) and is_valid(np2_r,np2_c):
                np = [(np1_r,np1_c),(np2_r,np2_c)]
                add_np(np,tmp_cnt)
        if tp1[0] == tp2[0]:  # 회전파트
            if is_valid(tp1[0]-1,tp1[1]) and is_valid(tp2[0]-1,tp2[1]):
                np = [(tp1[0],tp1[1]),(tp2[0]-1,tp2[1]-1)]
                add_np(np,tmp_cnt)
                np = [(tp1[0]-1,tp1[1]+1),(tp2[0],tp2[1])]
                add_np(np,tmp_cnt)
            if is_valid(tp1[0]+1,tp1[1]) and is_valid(tp2[0]+1,tp2[1]):
                np = [(tp1[0],tp1[1]),(tp2[0]+1,tp2[1]-1)]
                add_np(np,tmp_cnt)
                np = [(tp1[0]+1,tp1[1]+1),(tp2[0],tp2[1])]
                add_np(np,tmp_cnt)
        elif tp1[1] == tp2[1]:
            if is_valid(tp1[0],tp1[1]-1) and is_valid(tp2[0],tp2[1]-1):
                np = [(tp1[0],tp1[1]),(tp2[0]-1,tp2[1]-1)]
                add_np(np,tmp_cnt)
                np = [(tp1[0]+1,tp1[1]-1),(tp2[0],tp2[1])]
                add_np(np,tmp_cnt)
            if is_valid(tp1[0],tp1[1]+1) and is_valid(tp2[0],tp2[1]+1):
                np = [(tp1[0],tp1[1]),(tp2[0]-1,tp2[1]+1)]
                add_np(np,tmp_cnt)
                np = [(tp1[0]+1,tp1[1]+1),(tp2[0],tp2[1])]
                add_np(np,tmp_cnt)

배우게 된 점 [ 필수 X ]

※ set 에는 immutable 한 type 만 원소로 넣을 수 있다 ※

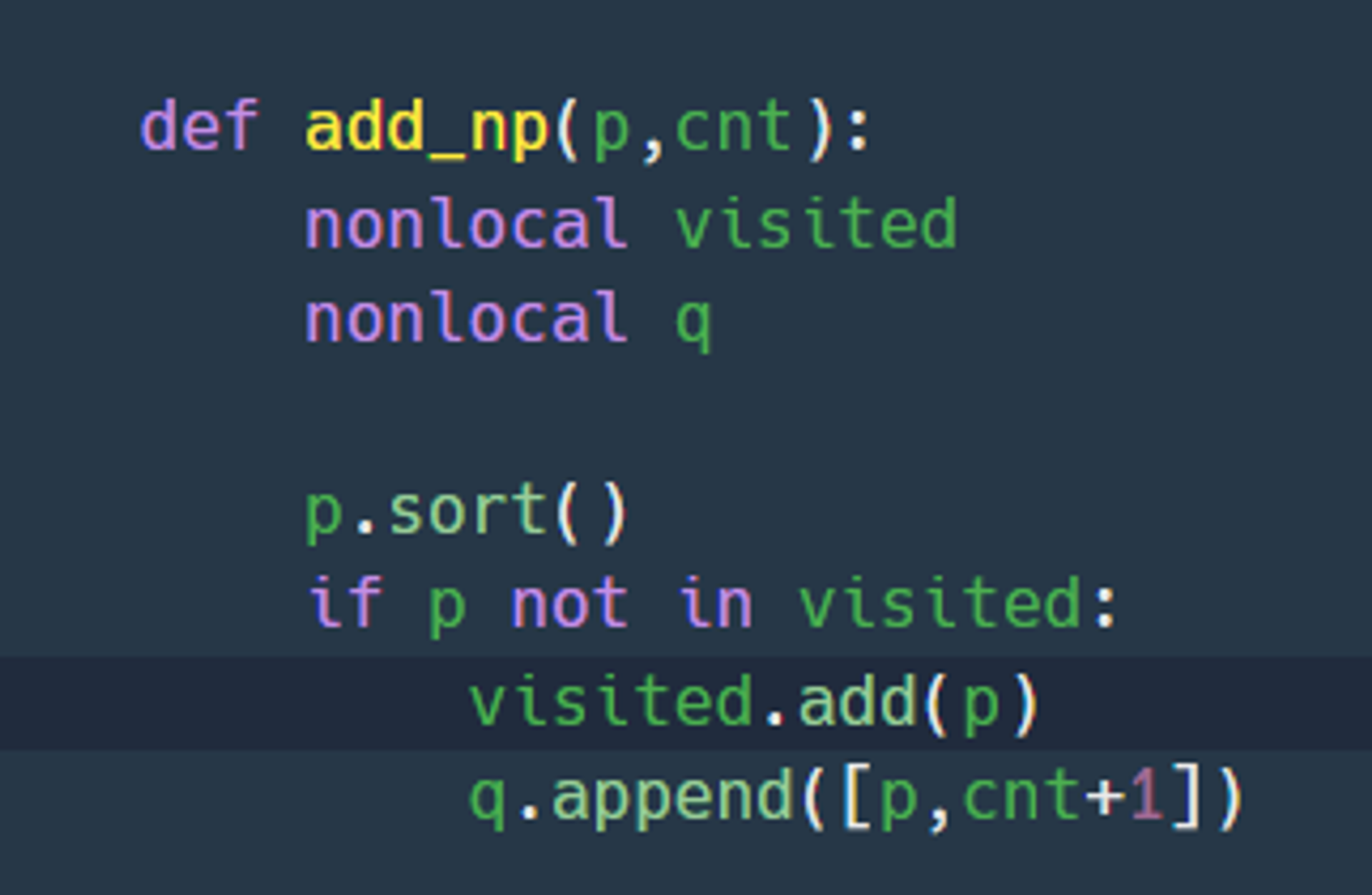
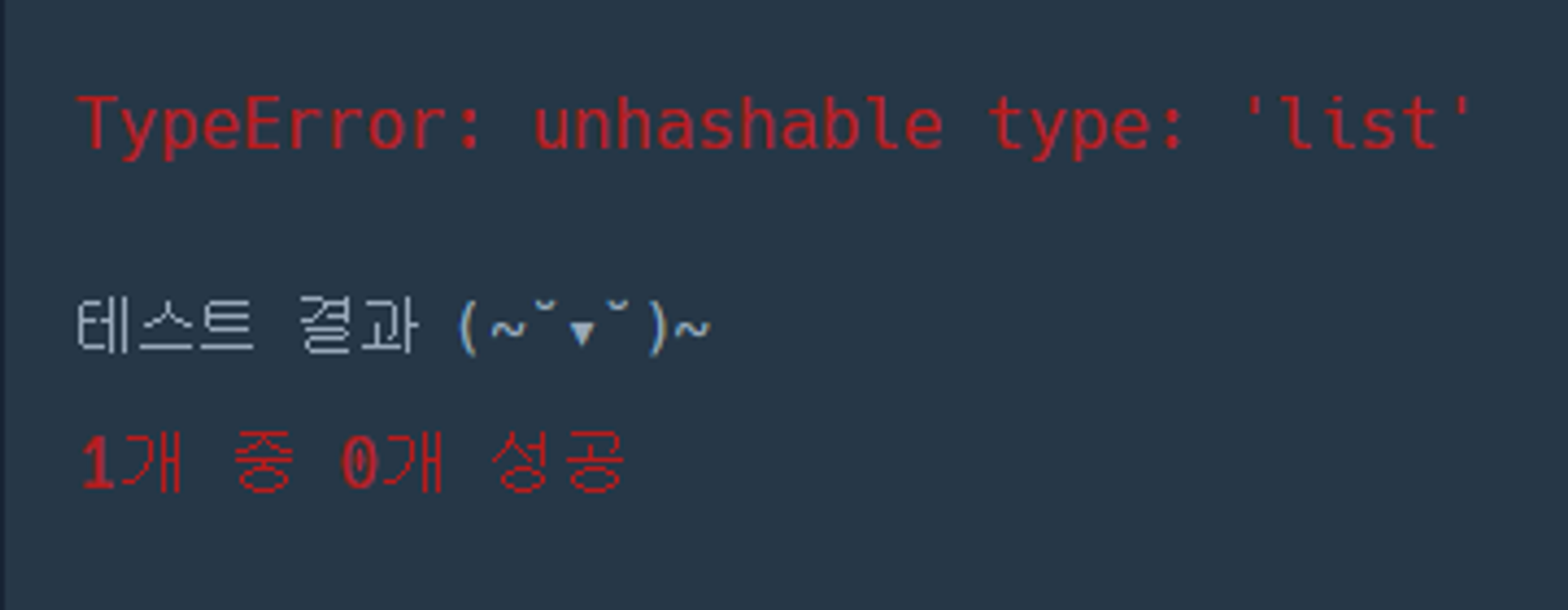
hashable 하다는 것은 어떤 데이터를 hash 함수를 이용해서 hash값으로 변환할 수 있다는 것을 의미한다.

hash는 어떤 특정 데이터에 대해서, 매우 유니크한 하나의 값을 가지게 된다.

그런데 원래 데이터가 변한다면, 이 데이터가 변함에 따라서 해당 hash 값은 의미가 없어진다.

따라서 특정 원소가 hashable 하기 위해서는 해당 원소는 immutable 해야 한다.

set 의 원소들은 이 hash값을 활용해서 각 원소들의 unique함을 보장한다.

따라서 set 의 원소들은 hashable 해야하고, 이는 즉, 각 원소들이 immutable 해야 한다는 것을 의미한다.

해시 가능한 데이터 형식은 딕셔너리의 키 또는 집합(set)의 원소로 사용될 수 있다.

list는 mutable 하기 때문에 hashble 하지 않다. 따라서, set 의 원소로 활용될 수 없다.

list형식을 set 의 원소로 활용하고 싶으면 해당 list 를 tuple 로 형변환하여 원소로 넣어주면 된다.

질문 [ 필수 X ]

Q1

어떻게 리팩토링하여 가독성을 높힐 수 있을지 잘 모르겠다.

피드백 [ 코치 작성 ]

A1

가독성을 위한 회전 함수 코드 분리의 예시는 다음과 같습니다.

def rotate(position_variable):
	if 가로:
		rotate_upside(position_variable):
		rotate_downside(position_variable):
	elif 세로:
		rotate_leftside(position_variable):
		rotate_rightside(position_variable):
	else:
		print("error")

위와 같이 코드를 세분화 하고 rotate_upside, rotate_downside, rotate_leftside, rotate_rightside함수를 따로 구현해 분리한다면 가독성 이 더 좋아질 것입니다. 또한 회전 함수에서 유사한 코드가 중복되긴 해도 해당 코드를 하나의 로직으로 통합하는 것은 다소 소요가 필요해 보이며 코딩 테스트의 관점에서 보았을 때 위 코드 정도의 함수 분리가 적절해 보입니다.

from collections import deque

def solution(board):
    N = len(board)
    answer = 0
    
    dr = [0,1,0,-1]
    dc = [1,0,-1,0]
    
    visited = set()
    q = deque([[[(0,0),(0,1)],0]])
    
    def is_valid(r,c):
        if 0 <= r < N and 0 <= c < N and board[r][c] == 0:
            return True
        return False
    
    def add_np(p,cnt):
        nonlocal visited
        nonlocal q
        
        p.sort()
        if tuple(p) not in visited:
            visited.add(tuple(p))
            q.append([p,cnt+1])
            
    def rotate_upside(tp1, tp2):
        if is_valid(tp1[0]-1,tp1[1]) and is_valid(tp2[0]-1,tp2[1]):
            add_np([(tp1[0],tp1[1]),(tp2[0]-1,tp2[1]-1)],tmp_cnt)
            add_np([(tp1[0]-1,tp1[1]+1),(tp2[0],tp2[1])],tmp_cnt)
            
    def rotate_downside(tp1, tp2):
        if is_valid(tp1[0]+1,tp1[1]) and is_valid(tp2[0]+1,tp2[1]):
            add_np([(tp1[0],tp1[1]),(tp2[0]+1,tp2[1]-1)],tmp_cnt)
            add_np([(tp1[0]+1,tp1[1]+1),(tp2[0],tp2[1])],tmp_cnt)
            
    def rotate_leftside(tp1, tp2):
        if is_valid(tp1[0],tp1[1]-1) and is_valid(tp2[0],tp2[1]-1):
            add_np([(tp1[0],tp1[1]),(tp2[0]-1,tp2[1]-1)],tmp_cnt)
            add_np([(tp1[0]+1,tp1[1]-1),(tp2[0],tp2[1])],tmp_cnt)

    def rotate_rightside(tp1, tp2):
        if is_valid(tp1[0],tp1[1]+1) and is_valid(tp2[0],tp2[1]+1):
            add_np([(tp1[0],tp1[1]),(tp2[0]-1,tp2[1]+1)],tmp_cnt)
            add_np([(tp1[0]+1,tp1[1]+1),(tp2[0],tp2[1])],tmp_cnt)
            
    def rotate(tp1,tp2):
        if tp1[0] == tp2[0]:
            rotate_upside(tp1, tp2)
            rotate_downside(tp1, tp2)
        elif tp1[1] == tp2[1]:
            rotate_leftside(tp1, tp2)
            rotate_rightside(tp1, tp2)      
    
    def parallel_move(tp1,tp2):
        for i in range(4):
            np1_r, np1_c = tp1[0]+dr[i], tp1[1]+dc[i]
            np2_r, np2_c = tp2[0]+dr[i], tp2[1]+dc[i]
            if is_valid(np1_r,np1_c) and is_valid(np2_r,np2_c):
                np = [(np1_r,np1_c),(np2_r,np2_c)]
                add_np(np,tmp_cnt)

    while q:
        [tp1, tp2],tmp_cnt = q.popleft()
        if tp1 == (N-1,N-1) or tp2 == (N-1,N-1):
            return tmp_cnt
        parallel_move(tp1, tp2)
        rotate(tp1,tp2)