[노씨데브 킬링캠프] 4주차 - 문제풀이 : ★Reachable Nodes In Subdivided Graph★

KissNode·2024년 2월 6일

노씨데브 킬링캠프

목록 보기

48/73

★Reachable Nodes In Subdivided Graph★

★다시 풀어봐야할 문제★ (해설코드보고 이해한 후 다시 풀어보았으나 최적화가 똥이었음)

https://leetcode.com/problems/reachable-nodes-in-subdivided-graph/description/

문제 파악 [필수 작성]

문제이해

무방향 그래프
0~n-1 노드
cnt 에 따라서 특정엣지위에 노드를 cnt 갯수만큼 생성했을때
노드0번에서 maxMoves 안에 도착할 수 있는 노드갯수가 몇개인지
알고싶다.

제한 조건 확인

이어진 엣지가 없어 더 확장을 못할때는 도달하지 못한다.
겹치냐 안겹치냐 구분하는게 어렵고, 직접 노드가 있는게
아니기 때문에 카운트하기가 어렵다.
엣지는 최소 10^4 최대 900만
두점을 잇는 엣지는 유일
사이에 노드는 최대 10^4 -> 즉, 직접 노드 추가해서 하지 말아라는 의미
maxMoves 최대 10^9 -> 직접 하나씩 카운팅하지말고 엣지사이에 숫자많을때 한방에 처리하라는 의미
노드는 최대 3000개

아이디어

구상이 어려운점은 엣지위의 구간이 겹쳤을때 어떻게 겹친부분만큼 제거해줄 수 있는가
두 노드를 잇는 엣지는 무조건 1개 라고 했으니까 무조건 양쪽끝에서부터 전파가된다.
만약 특정엣지의 길이가 10이고, 5만큼 사용했으면, 5만큼 남았다고 얘기할수있고
반대편에서 5이상으로, 예를들어 13만큼 전파하려하면 5만큼만 새로운노드가 추가되고, 13에서 10+1만큼빼서
다음 노드에 2만큼의 에너지를 전달해주면 된다.

특정 노드는 각각 자신의 남은 에너지(전파될수있는 범위, 즉, maxMoves)를 가지고 있음
만약 자신과 이어진 엣지길이+도착노드의 값이 내가 가진 에너지보다 더 작으면 해당 엣지의 남은노드갯수를 0개로 바꾸고
도착노드에 이전에 가진 에너지 - 이어진 길이- 1 만큼 업데이트해준다.
만약 자신과 이어진 엣지길이 + 도착노드의 값이 내가 가진 에너지보다 더 크면 해당 엣지의 남은 노드갯수를
엣지길이 - 내 에너지로 업데이트해주고 내 에너지만큼 결과에 더해주고 다음노드를 추가하지 않는다.
굳이 힙이 필요하지 않은 문제?

시간복잡도

자료구조

엣지의 정보를 key:출발노드, value:[]도착노드,실제길이,남은노드갯수]형식으로 저장해주어야 함.
충전된 노드 결과값은 누적합 형태로 진행되어야 함.

접근 방법 [필수 작성]

아이디어

코드 구현 [필수 작성]

1차시도 (1시간30분 소요)

아예 로직자체가 잘못됨

얼마나 더 뻗어나갈수있냐로 생각했는데

뻗어나가는 방향이 노드 양쪽에서 될수가 있어서 너무 복잡해짐
코너케이스가 너무 많음
겹치는 케이스를 적절히 조절해줘야함

→ 아이디어가 너무 복잡하고 길을 잃어서 해설코드 봄

from collections import deque
from collections import defaultdict
class Solution:
    def reachableNodes(self, edges: List[List[int]], maxMoves: int, n: int) -> int:
        visited = [1 for _ in range(n)]
        visited_node_num = 0
        q = deque([])
        nn_info = [[] for _ in range(n)]
        edges_info = dict()
        for i in range(n):
            edges_info[i] = [[] for _ in range(n)] 
        for edge in edges:
            nn_info[edge[0]].append(edge[1])
            nn_info[edge[1]].append(edge[0])
            edges_info[edge[0]][edge[1]].append([edge[2],edge[2]])
            edges_info[edge[1]][edge[0]].append([edge[2],edge[2]])
        
        visited_node_num += 1
        visited[0] = 0
        q.append([0,maxMoves])

        while q:
            #print("edges_info=",edges_info)
            #print("visited_node_num=",visited_node_num)
            #print("q=",q)
            tn,te = q.popleft() #tmp_node, tmp_energy
            for nn in nn_info[tn]: #next_node, max_edge_len, tmp_left_node
                mel,tln = edges_info[tn][nn][0]
                if te - mel - 1 > 0 :
                    if visited[nn] == 1:
                        q.append([nn, te - mel - 1])
                        #print("added:",edges_info[tn][nn][0][1] + visited[nn])
                        visited_node_num += edges_info[tn][nn][0][1] + visited[nn]
                        visited[nn] = 0
                        edges_info[tn][nn][0][1] = 0
                        edges_info[nn][tn][0][1] = 0
                elif te - mel - 1 == 0:
                    #print("added:",edges_info[tn][nn][0][1] + visited[nn])
                    visited_node_num += edges_info[tn][nn][0][1] + visited[nn]
                    visited[nn] = 0
                    edges_info[tn][nn][0][1] = 0
                    edges_info[nn][tn][0][1] = 0
                else:
                    if edges_info[tn][nn][0][1] > te:
                        #print("added:",te)
                        visited_node_num += te
                        edges_info[tn][nn][0][1] -= te
                        edges_info[nn][tn][0][1] -= te
                    elif edges_info[tn][nn][0][1] <= te:
                        #print("added:",edges_info[tn][nn][0][1])
                        visited_node_num += edges_info[tn][nn][0][1]
                        edges_info[tn][nn][0][1] = 0
                        edges_info[nn][tn][0][1] = 0

        return visited_node_num

해설코드

from collections import defaultdict
from heapq import heappush, heappop
class Solution:
    def reachableNodes(self, edges: List[List[int]], maxMoves: int, n: int) -> int:
				#✅ 인풋을 본인이 쓰기 편한 구조로 바꾸기(다익스트라) => 무방향 그래프 만들기
        reachable_node_num, reachable_subnode_num = 0, 0
        graph = defaultdict(list)
        for u, v, w in edges:
            graph[u].append([v, w])
            graph[v].append([u, w])

				#✅ 가중치 합이 maxMoves보다 높아질때까지 다익스트라를 진행
        dist = [maxMoves + 1 for _ in range(n)]
        dist[0] = 0
        heap = []
        heappush(heap, (0, 0))
        while heap:
            cur_dist, cur_loc = heappop(heap)
            if maxMoves <= dist[cur_loc]:
                break
            for new_v, new_w in graph[cur_loc]:
                new_dist = cur_dist + new_w + 1
                if new_dist < dist[new_v]:
                    dist[new_v] = new_dist
                    heappush(heap, (new_dist, new_v))

				#✅ 원본 그래프에 있던 노드에서 도달 가능한 개수 계산
        for d in dist:
						#✅ 원본 그래프에 있던 노드까지의 거리가 maxMoves보다 작거나 같다면 도달 가능
            if d <= maxMoves:
                reachable_node_num += 1

				#✅ 세분화된 그래프에서 원본그래프 노드를 제외한 세분화노드들 중 도달가능한 개수 계산
        for u, v, sub_node_num in edges:
            a, b = 0, 0
						#✅ 간선[u,v]에 대해 maxMoves, dist[u], dist[v], cnt[u,v]를 통해 도달 가능한 노드 계산
            if dist[u] <= maxMoves:
                a = min(maxMoves - dist[u], sub_node_num)
            if dist[v] <= maxMoves:
                b = min(maxMoves - dist[v], sub_node_num)
            reachable_subnode_num += min(a + b, sub_node_num)
    
        return reachable_node_num + reachable_subnode_num

2차 시도

1차 시도에서는 엣지위 노드부분과 원래 노드부분을 동시에 처리해주려해서 어려웠다.

또, 해설코드는 최소로 도착할 수 있는 값들을 저장해주었는데,

나는 각 노드가 최대로 뻗어나갈 수 있는 범위를 저장해서 문제를 다시 풀어보려고 한다.

각 노드를 탐색하면서 각 노드가 가질 수 있는 최대 maxMoves 를 저장해준다.

→ 최적화가 똥이다… 어떻게하면 노드탐색시간을 줄여줄 수 있을지 생각해보자.

from collections import defaultdict
from collections import deque

class Solution:
    def reachableNodes(self, edges: List[List[int]], maxMoves: int, n: int) -> int:
        node_maxMoves = [-1 for _ in range(n)]
        q = deque([])
        edges_dict = defaultdict(list)
        for edge in edges:
            u,v,w = edge
            edges_dict[u].append([v,w])
            edges_dict[v].append([u,w])
        
        node_maxMoves[0] = maxMoves
        q.append([0,maxMoves])

        while q:
            #print("q:",q)
            tn,tm = q.popleft()
            for next_edge in edges_dict[tn]:
                nn, w = next_edge
                if node_maxMoves[nn] < tm-w-1:
                    node_maxMoves[nn] = tm-w-1
                    q.append([nn,node_maxMoves[nn]])

        main_node_cnt = 0
        for elem in node_maxMoves:
            if elem > -1:
                main_node_cnt += 1

        #print(main_node_cnt)
        #print(node_maxMoves)

        sub_node_cnt = 0
        for u,v,w in edges:
            if node_maxMoves[u] == -1 and node_maxMoves[v] == -1:
                continue
            elif node_maxMoves[u] != -1 and node_maxMoves[v] == -1:
                if node_maxMoves[u] >= w:
                    sub_node_cnt += w
                else:
                    sub_node_cnt += node_maxMoves[u]
            elif node_maxMoves[u] == -1 and node_maxMoves[v] != -1:
                if node_maxMoves[v] >= w:
                    sub_node_cnt += w
                else:
                    sub_node_cnt += node_maxMoves[v]
            elif node_maxMoves[u] != -1 and node_maxMoves[v] != -1:
                if node_maxMoves[u] + node_maxMoves[v] >= w:
                    sub_node_cnt += w
                else:
                    sub_node_cnt += node_maxMoves[u] + node_maxMoves[v]

	        return main_node_cnt + sub_node_cnt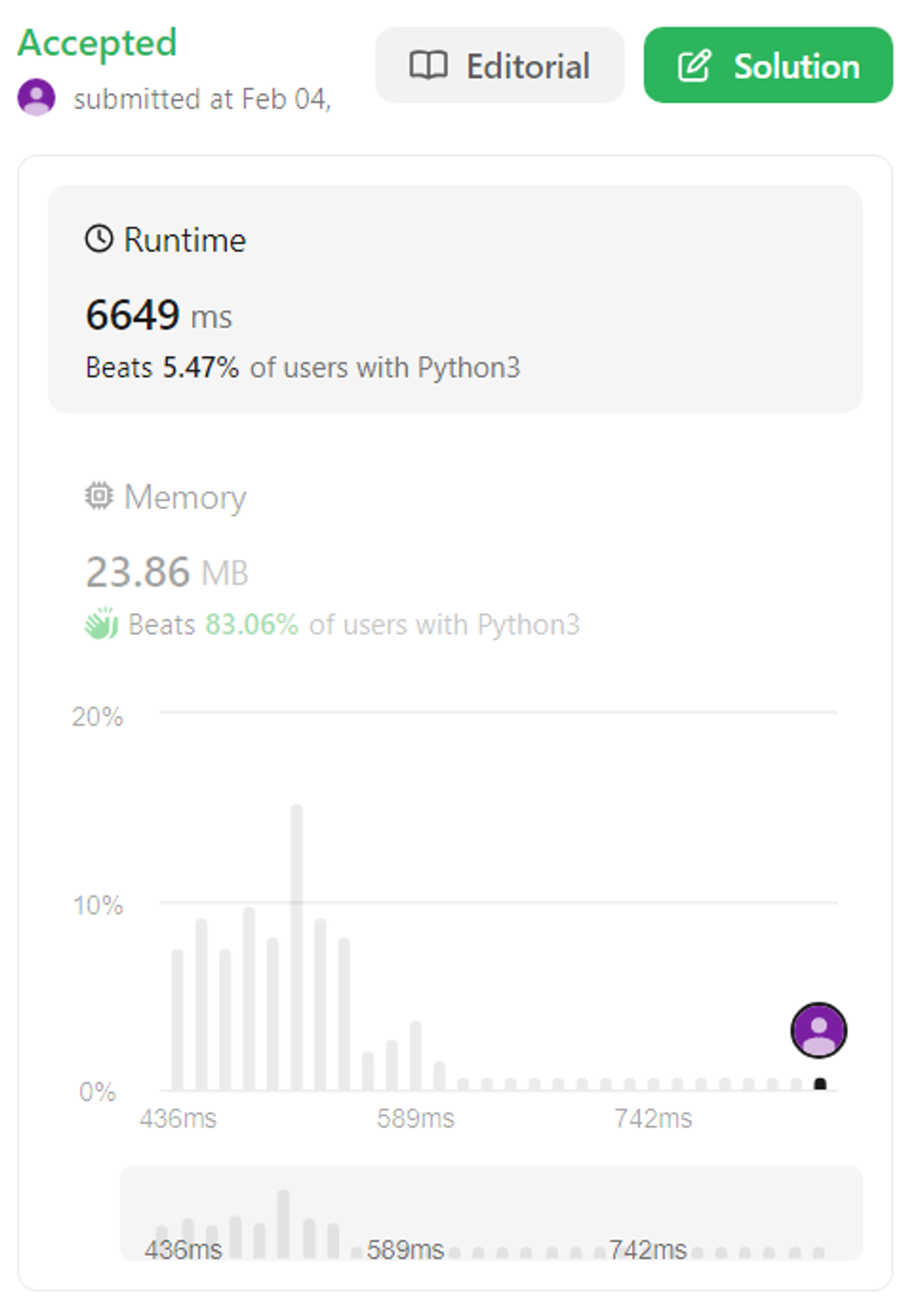

3차 시도

while문에서 각 노드의 모든 엣지에 대해 돌기때문에 생기는 문제로 파악되나

해당 노드까지의 거리를 계산해보지 않고서는 maxMoves 를 구할 수 있는 방법이 없기에

최적화 방법이 떠오르지 않음

그래서 해설코드랑 비교해보았는데

해설코드는 heap을 사용해서 최솟값부터 처리하고, maxMoves 가 넘어가면

break 해주는걸 발견함

break 때문에 시간효율성이 증대되는걸로 보여서 나도 자료구조를 heap을

사용했는데 break 때문에 그런것이 아니라, heap을 사용하는것만으로도

엄청난 최적화를 이룸. 근데 왜 그런효과를 내는지 직관적으로 잘 이해가 안감

→ 생각해보니 heap 을 사용하여 최대값을 가진것부터 처리해주면 순서없이 그냥 마구잡이로 처리하는 것을 할때 후반부에 가서 불필요하게 반복되어 덮여쓰여지는 상당수 부분을 제거할 수 있음. 그래서 deque의 삽입삭제가 O(1) 의 시간복잡도를 가지지만, edge 도 많아봐야 O(log10^4) = O(log 2^14) = O(14)

정확한 시간복잡도는 어떻게 계산할 수 있을까?

또 오히려 break 구문을 넣어주면 히든테케들을 통과를 못함. 잘 이해가 안감.

from collections import defaultdict
from collections import deque

class Solution:
    def reachableNodes(self, edges: List[List[int]], maxMoves: int, n: int) -> int:
        node_maxMoves = [-1 for _ in range(n)]
        q = deque([])
        edges_dict = defaultdict(list)
        for edge in edges:
            u,v,w = edge
            edges_dict[u].append([v,w])
            edges_dict[v].append([u,w])
        
        node_maxMoves[0] = maxMoves
        q.append([0,maxMoves])

        while q:
            #print("q:",q)
            tn,tm = q.popleft()
            for next_edge in edges_dict[tn]:
                nn, w = next_edge
                if node_maxMoves[nn] < tm-w-1:
                    node_maxMoves[nn] = tm-w-1
                    q.append([nn,node_maxMoves[nn]])

        main_node_cnt = 0
        for elem in node_maxMoves:
            if elem > -1:
                main_node_cnt += 1

        sub_node_cnt = 0
        for u,v,w in edges:
            if node_maxMoves[u] == -1 and node_maxMoves[v] == -1:
                continue
            elif node_maxMoves[v] == -1:
                sub_node_cnt += min(w,node_maxMoves[u])
            elif node_maxMoves[u] == -1:
                sub_node_cnt += min(w,node_maxMoves[v])
            else:
                sub_node_cnt += min(w,node_maxMoves[u] + node_maxMoves[v])
                
        return main_node_cnt + sub_node_cnt

heap으로 바꾼 코드

from collections import defaultdict
import heapq

class Solution:
    def reachableNodes(self, edges: List[List[int]], maxMoves: int, n: int) -> int:
        node_maxMoves = [-1 for _ in range(n)]
        max_heap = []
        edges_dict = defaultdict(list)
        for edge in edges:
            u,v,w = edge
            edges_dict[u].append([v,w])
            edges_dict[v].append([u,w])
        
        node_maxMoves[0] = maxMoves
        max_heap.append([-maxMoves,0])

        while max_heap:
            #print("max_heap:",max_heap)
            tm,tn = heapq.heappop(max_heap)
            tm *= -1
            for next_edge in edges_dict[tn]:
                nn, w = next_edge
                if node_maxMoves[nn] < tm-w-1:
                    node_maxMoves[nn] = tm-w-1
                    max_heap.append([-node_maxMoves[nn],nn])

        main_node_cnt = 0
        for elem in node_maxMoves:
            if elem > -1:
                main_node_cnt += 1

        sub_node_cnt = 0
        for u,v,w in edges:
            if node_maxMoves[u] == -1 and node_maxMoves[v] == -1:
                continue
            elif node_maxMoves[v] == -1:
                sub_node_cnt += min(w,node_maxMoves[u])
            elif node_maxMoves[u] == -1:
                sub_node_cnt += min(w,node_maxMoves[v])
            else:
                sub_node_cnt += min(w,node_maxMoves[u] + node_maxMoves[v])
                
        return main_node_cnt + sub_node_cnt

heap 에 break 구문까지 삽입해준 경우 → 99.45% beat 하는 최적화 달성!

from collections import defaultdict
import heapq

class Solution:
    def reachableNodes(self, edges: List[List[int]], maxMoves: int, n: int) -> int:
        node_maxMoves = [-1 for _ in range(n)]
        max_heap = []
        edges_dict = defaultdict(list)
        for edge in edges:
            u,v,w = edge
            edges_dict[u].append([v,w])
            edges_dict[v].append([u,w])
        
        node_maxMoves[0] = maxMoves
        max_heap.append([-maxMoves,0])

        while max_heap:
            #print("max_heap:",max_heap)
            tm,tn = heapq.heappop(max_heap)
            tm *= -1
            if tm <= 0:
                break
            for next_edge in edges_dict[tn]:
                nn, w = next_edge
                if node_maxMoves[nn] < tm-w-1:
                    node_maxMoves[nn] = tm-w-1
                    heapq.heappush(max_heap,[-node_maxMoves[nn],nn])

        main_node_cnt = 0
        for elem in node_maxMoves:
            if elem > -1:
                main_node_cnt += 1

        sub_node_cnt = 0
        for u,v,w in edges:
            if node_maxMoves[u] == -1 and node_maxMoves[v] == -1:
                continue
            elif node_maxMoves[v] == -1:
                sub_node_cnt += min(w,node_maxMoves[u])
            elif node_maxMoves[u] == -1:
                sub_node_cnt += min(w,node_maxMoves[v])
            else:
                sub_node_cnt += min(w,node_maxMoves[u] + node_maxMoves[v])
                
        return main_node_cnt + sub_node_cnt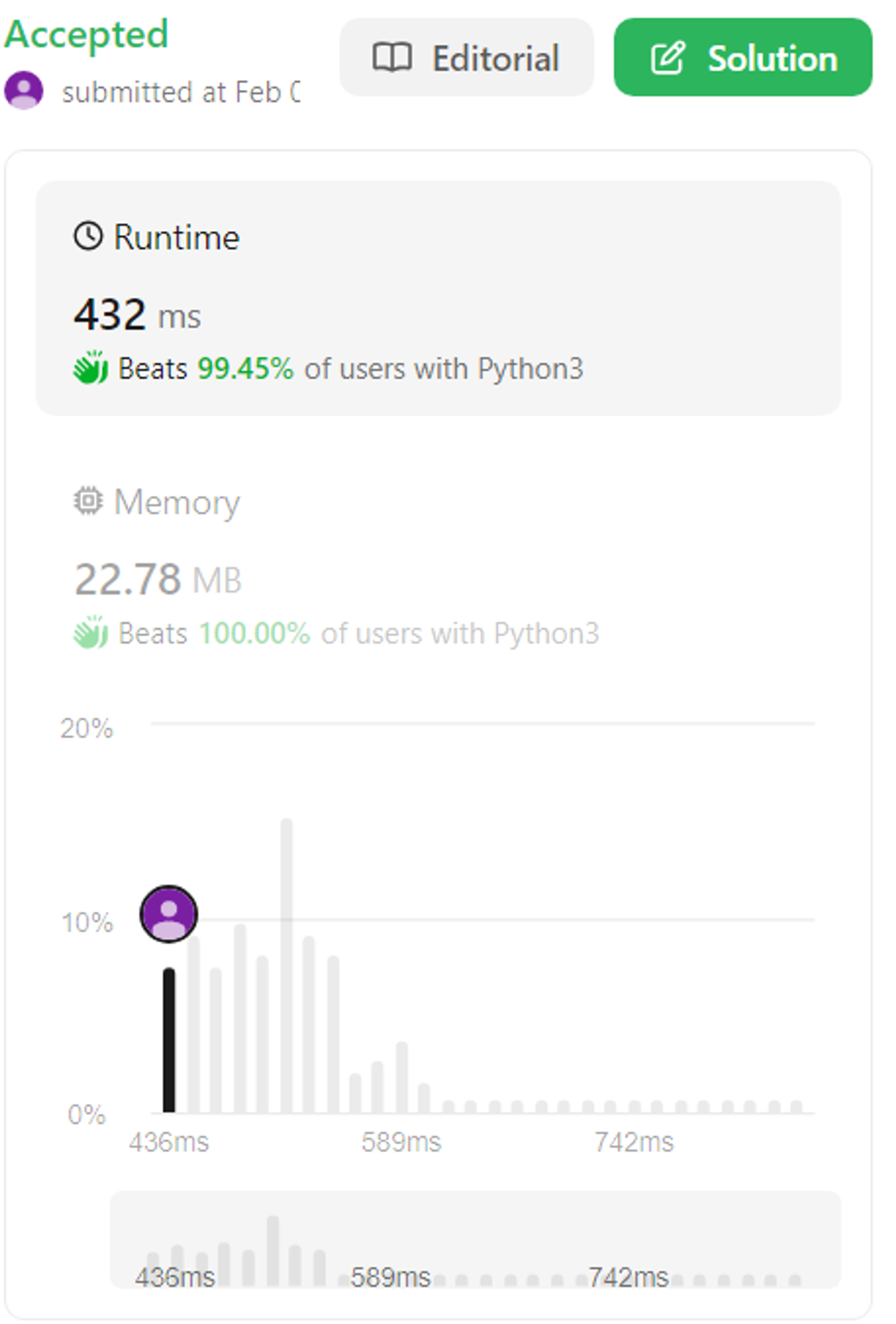

배우게 된 점 [필수 작성]

다익스트라 알고리즘을 쓰는 이유

가중치가 없는 그래프에서는 BFS 가 한칸씩 퍼져나간다는 점에서 의미가 있지만, 가중치가 있는 그래프에서는 BFS 가 의미가 없다. 이때, 힙을 활용한 다익스트라 알고리즘을 사용하면, 목적에 맞게 가장 크거나, 가장 작은 값부터 순차적으로 처리해줄 수 있기 때문에, 선후관계를 지키지 않았을때 생기는 중복되는 상당수 부분을 생략해줄 수 있게 된다.

이중리스트처럼 이중딕셔너리 또한 구현가능하다.

복잡한 문제일수록 분할해서 생각하자.

해설코드의 핵심은 엣지위의 노드 처리부분과 기존 노드 처리를 구분했다는 점에서 의미가 크다.

결국 어려운 파트는 엣지위의 노드 처리부분이기 때문에 해당 부분을 분리해서 생각하면 좀 더 문제 접근이 쉬워질 수 있다.

스터디 통해 배우게 된점

maxsize 말고도, float(”inf”) 를 통해서 무한대라는 값을 줄 수 있다. 디버깅할때도 실제로 inf 로 찍히기 때문에 좀 더 명확하다.
만약 실제 테스트 케이스에 악의적으로 maxsize 값을 활용하는 테스트케이스가 들어오면 알고리즘은 정상작동 할 수 있을까? 예를들어, 방문여부를 체크하는 리스트를 maxsize 로 초기화했는데, maxsize 값이 들어온다면? → 보통 문제에서 input 값의 범위를 제시해주기 때문에, 해당 범위보다 +1 인 값들로 초기화하는 것을 생각하면, 이런 걱정을 안해도 되는것을 알 수 있다.

질문 [ 필수 X ]

Q1

리트코드에서 보이는 RunTime 은 모든 실제 테스트케이스를 돌리는데 걸리는 시간인가요? 아니면 하나의 테스트케이스를 돌리는데 걸리는 평균 시간인가요? 후자가 맞겠죠?

A1

후자가 맞다. 추론하건데, 사이트마다 동작방식에 따라 runtime 계산 방식은 다를 수 있지만, leetcode 의 경우 예시 테스트 케이스를 만들때 예상 output 값을 넣어주는 칸이 없으며, 예시 테스트 케이스들과 실제 테스트 케이스들을 평가하는 방법은 같다고 추론할 수 있다. 또한, 예시 테스트 케이스들을 아무리 늘려도, runtime 은 동일하게 나오기때문에 전체 소요 시간이 아닌 모든 테스트 케이스의 런타임에 대한 평균시간임을 알 수 있다.

Q2

3차 시도

생각의 흐름이 맞는지 궁금합니다. 그리고 정확한 시간복잡도 계산은 어떻게 하면 좋을까요? deque 로 구현할때와 max_heap 으로 구현할때 각각에 대해서 설명해주실수 있나요?

제가 생각했을땐,

deque 의 경우는 모든 노드의 모든 엣지에 대해서 탐색을 진행하고, 또, 이어질 경우 꼬리에 꼬리를 물고 그 경우가 길어져, 더 큰 값이 발견되면 덮어씌워지는 경우가 엄청나게 반복될 것으로 보이고,

max_heap 의 경우는 모든 노드의 모든엣지에 대해서 탐색을 진행하지만, 큰값부터 순차적으로 처리하기에 heap 삽입삭제에 소요되는 시간이 deque 보다는 크고, 덮여씌워지는 경우도 여전히 존재하지만, 덮여씌워지는 경우가 상당부분 줄어 삽입삭제 또한 상당부분 줄기때문에 deque 로 구현한것보다 더 좋은 성능을 보이지 않나 싶습니다.

하지만, 코드상으로 보았을때 로직이 완전히 동일하여 시간복잡도가 다를 수 있는건가 하는 의문이 듭니다.

deque 구현

while q:
    #print("q:",q)
    tn,tm = q.popleft()
    for next_edge in edges_dict[tn]:
        nn, w = next_edge
        if node_maxMoves[nn] < tm-w-1:
            node_maxMoves[nn] = tm-w-1
            q.append([nn,node_maxMoves[nn]])

heap 구현

while max_heap:
		#print("max_heap:",max_heap)
		tm,tn = heapq.heappop(max_heap)
		tm *= -1
		for next_edge in edges_dict[tn]:
		    nn, w = next_edge
		    if node_maxMoves[nn] < tm-w-1:
		        node_maxMoves[nn] = tm-w-1
		        heapq.heappush(max_heap,[-node_maxMoves[nn],nn])

A2

내가 적은 생각의 흐름이 맞고, 엄밀하게 시간복잡도를 계산하는 것은 어렵다. 왜냐하면 시간복잡도를 구하려면 의사결정트리의 깊이를 알아야하는데, 이때, 의사결정트리의 깊이는 edge들의 weight 에 의해 크게 달라지기 때문이다. 또한, 모든 edge 가 1이고, maxMoves 가 최대인 경우는 문제에서 풀고자하는 문제와 동떨어진 문제여서 시간복잡도를 계산하는게 의미가 없어진다. 즉, deque 로 구현한 문제풀이 방법은 실제 문제에서 의도한 풀이와 다른 방법이고, 만약 악의적인 테스트케이스가 주어진다면, 통과를 못하게될 수 도 있는 풀이방법이다. 스도쿠 문제처럼 우리가 완벽하게 연산시간을 계산할 수는 없는 경우와 비슷한 맥락이라고 볼 수 있다.

Q3 (추가질문)

혹시 이중 딕셔너리를 활용하는 문제도 코테에서 출제된 적이 있나요?

이제껏 문제에서 이중 딕셔너리를 사용해야만 하는 경우는 한번도 접해보지 못한것같아서, 만약 이중 딕셔너리를 사용해야하는 경우라면 어떤 경우의 문제, 또는 어떤 유형의 문제에서 활용되게 될까요?

답변

제 경험상으로는 “중첩 딕셔너리를 사용해서 풀어라!” 하고 주는 문제는 없었습니다. 하지만 다른 코딩 테스트 문제들이 모두 그렇듯 한 가지 풀이 방법만 있는 것이 아니며 하나의 풀이 방법에 대해서도 수없이 다양한 구현 방법들이 나올 수 있습니다. 그렇기에 중첩 딕셔너리의 사용에 대해서는 개인이 판단하는 영역입니다.

중첩 딕셔너리를 활용하게 될만한 문제라면 다음과 같습니다. 그래프가 주어진 상태에서 각각의 노드가 또다른 각각의 노드에 대한 정보를 저장해야 하는 경우 그래프의 각 노드가 담긴 딕셔너리에 각각의 노드에 대한 정보를 저장하는 딕셔너리를 value로 사용해 중첩 딕셔너리를 사용할 수 있습니다. 하지만 이 또한 각각의 노드에 대한 정보를 리스트로 저장해 인덱스를 통해 접근하는 방식을 택한다면 리스트를 value로 갖는 딕셔너리가 될 것이고 각각의 노드에 대한 정보를 클래스로 구현해둔다면 클래스를 value로 갖는 딕셔너리가 될 것입니다. 즉 구현에서 발생하는 차이가 될 뿐 반드시 중첩 딕셔너리를 사용해야만 하는 문제는 없을 것으로 판단됩니다.

KissNode

어제보다 더, 내일보다 덜.

이전 포스트

[노씨데브 킬링캠프] 4주차 - 문제풀이 : course schedule 2

다음 포스트

[노씨데브 킬링캠프] 4주차 - 문제풀이 : ★Reachable Nodes In Subdivided Graph★