★합승택시요금★
https://school.programmers.co.kr/learn/courses/30/lessons/72413
★다시 풀어볼 문제★(예전에 한번 풀었던건데 다시 풀려니 안풀린다…)
예전에 풀었던 기록 저장
아이디어
최저이동경로
다익스트라로 구현
s 에서 a를 먼저갔다가 a 에서 b 가는 경우 -> case1
s 에서 b를 먼저갔다가 b 에서 a 가는 경우 -> case2
s 에서 a + s 에서 b 가는 경우 -> case3
case 1,2,3 중 최소값 리턴
플로이드와샬 구현
2차원배열에서
3중포문구현
플로이드와샬(s,m,e):
2차원 배열 생성
무한대로 초기화
자기자신으로 가는거 0 으로 초기화
for i in range(len(s)):
for j in range(len(e)):
for k in range(len(m)):
matrix[s][e] = min(matrix[s][e], matrix[s][m]+matrix[m][e])
시간복잡도
O(V^3) = 8,000,000
암기목록
MST(모든노드를 잇는 최소간선)
다익스트라(한노드에서 다른노드로갈때 최소간선)
플루이드와샬(모든노드에서 모든노드로 갈때 최소간선)
import sys
def solution(n, s, a, b, fares):
#print(s,a,b)
answer = 0
INF = sys.maxsize
matrix = [[INF]*(n+1) for _ in range(n+1)]
for i in range(1,n+1):
matrix[i][i] = 0
for st,ed,c in fares:
matrix[st][ed] = c
matrix[ed][st] = c
for k in range(1,n+1):
for i in range(1,n+1):
for j in range(1,n+1):
matrix[i][j] = min(matrix[i][j], matrix[i][k] + matrix[k][j])
def hapseung(s,a,b):
#print(s,a,b)
cost = matrix[s][a]+matrix[s][b]
for m in range(1,n+1):
cost = min(cost,matrix[s][m]+matrix[m][a]+matrix[m][b])
#print(cost,matrix[s][m]+matrix[m][a]+matrix[m][b])
return cost
answer = hapseung(s,a,b)
return answer문제 파악 [필수 작성]
문제이해
각 지점 인덱스는 1부터N 까지
양방향 가중치 그래프 -> 다익스트라?
출발지 도착지는 달라질 수 있음
제한 조건 확인
S,A,B 는 다 다른 노드다
엣지는 최대 200*200/2 -> 약 2만개
두 노드를 잇는 엣지는 유일
아이디어
각 도착지에 도달할 수 있는 최저요금을 알아야함
각 도착지에 도달하는 최저요금의 경로가 동승시 최저요금의 경로를 보장하는가?
-> 보장하지 못한다.
혼자 타는 경우에는
min_heap 을 이용하여 구현하는 다익스트라의 특성상
먼저 도달하는 노드가 최소비용으로 갈 수 있는 노드임을 보장하지만,
같이 타는 경우는 돌아가더라도 두명의 합을 줄일 수 있는 경우가 있다.
1차 아이디어
case #1
두명의 집을 잇는 최소 경로 비용 +
S지점에서 두명 집을 잇는 최소 경로중 어느 노드에든 도달할 수 있는 경로 비용
과
case#2
각각 따로 갔을때 최소 비용을 비교해서
구현방법은
case #1 의 경우
A에서 B로 갈때 드는 비용과 경로를 알아야함
A를 min_heap 에 넣고 다음노드를 방문할 때마다
방문경로를 dict 형태로 저장 -> 경로dict key: 도착노드 , value: 출발노드
만약 도착노드가 B이면 경로dict 에서 key->value 트래킹으로 경로를 역추적해서
set 에 저장
그리고 S에서 set에 든 어느 원소하나라도 발견될때까지 다익스트라 시전
이렇게 하면 동승시 최소금액합을 구할 수 있음
case#2 의 경우
일반적인 다익스트라 시전 후 도착 노드가 A거나 B이면 해당하는 두 노드 가중치 합 구할 수 있음
case#1 case#2 비교후 더 적은값 리턴
시간복잡도
다익스트라 시간복잡도 (V+E)log(V) 인데 다익스트라 두번 돌리는 것과 동일하기 때문에
시간복잡도는 그냥 (V+E)log(V) 이고,
V는 최대 200
E는 최대 4만 이므로,
40200log(200) = 40,200 8 = 32만 -> 시간 충분
자료구조
접근 방법 [필수 작성]
코드 구현 [필수 작성]
1차 제출 (1시간 15분 소요)
뭔가 플로이드와샬로 푸는것 같은데 그냥 다익스트라로 한번 풀어보려하다가 코드가 엄청 길어지고 불필요한 자료구조가 늘어나면서 코드가 복잡해짐
예시 테케는 다 통과하나 실제 테케에서 대다수가 틀림, 코너케이스에 대해서 생각 필요
→
import heapq
def solution(n, s, a, b, fares):
path_dict = {}
path_node = []
edges = [[] for _ in range(n+1)]
for c,d,f in fares:
edges[c].append([f,d])
edges[d].append([f,c])
a_to_b_w = [-1 for _ in range(n+1)]
node_w = [-1 for _ in range(n+1)]
a_to_b_w[a] = 0
min_heap = []
heapq.heappush(min_heap,[0,a])
flag = 0
while min_heap:
if flag == 1:
break
tw, tn = heapq.heappop(min_heap)
for mw,nn in edges[tn]:
if a_to_b_w[nn] == -1:
a_to_b_w[nn] = mw + tw
heapq.heappush(min_heap,[a_to_b_w[nn],nn])
path_dict[nn] = tn
if nn == b:
flag = 1
break
path_node.append(b)
tmp_node = path_dict[b]
while True:
try:
path_node.append(tmp_node)
tmp_node = path_dict[tmp_node]
except:
break
node_w[s] = 0
min_heap = []
heapq.heappush(min_heap,[0,s])
while min_heap:
tw, tn = heapq.heappop(min_heap)
for mw,nn in edges[tn]:
if node_w[nn] == -1:
node_w[nn] = mw + tw
heapq.heappush(min_heap,[node_w[nn],nn])
min_together_fares = float("inf")
for node in path_node:
min_together_fares = min(min_together_fares,node_w[node])
min_together_fares += a_to_b_w[b]
min_solo_fares = node_w[a] + node_w[b]
#print("path_node: ",path_node)
#print("min_together_fares: ",min_together_fares)
#print("min_solo_fares: ",min_solo_fares)
#print("a_to_b_w[b]: ",a_to_b_w[b])
#print("node_w[a]: ",node_w[a])
#print("node_w[b]: ",node_w[b])
return min(min_together_fares,min_solo_fares)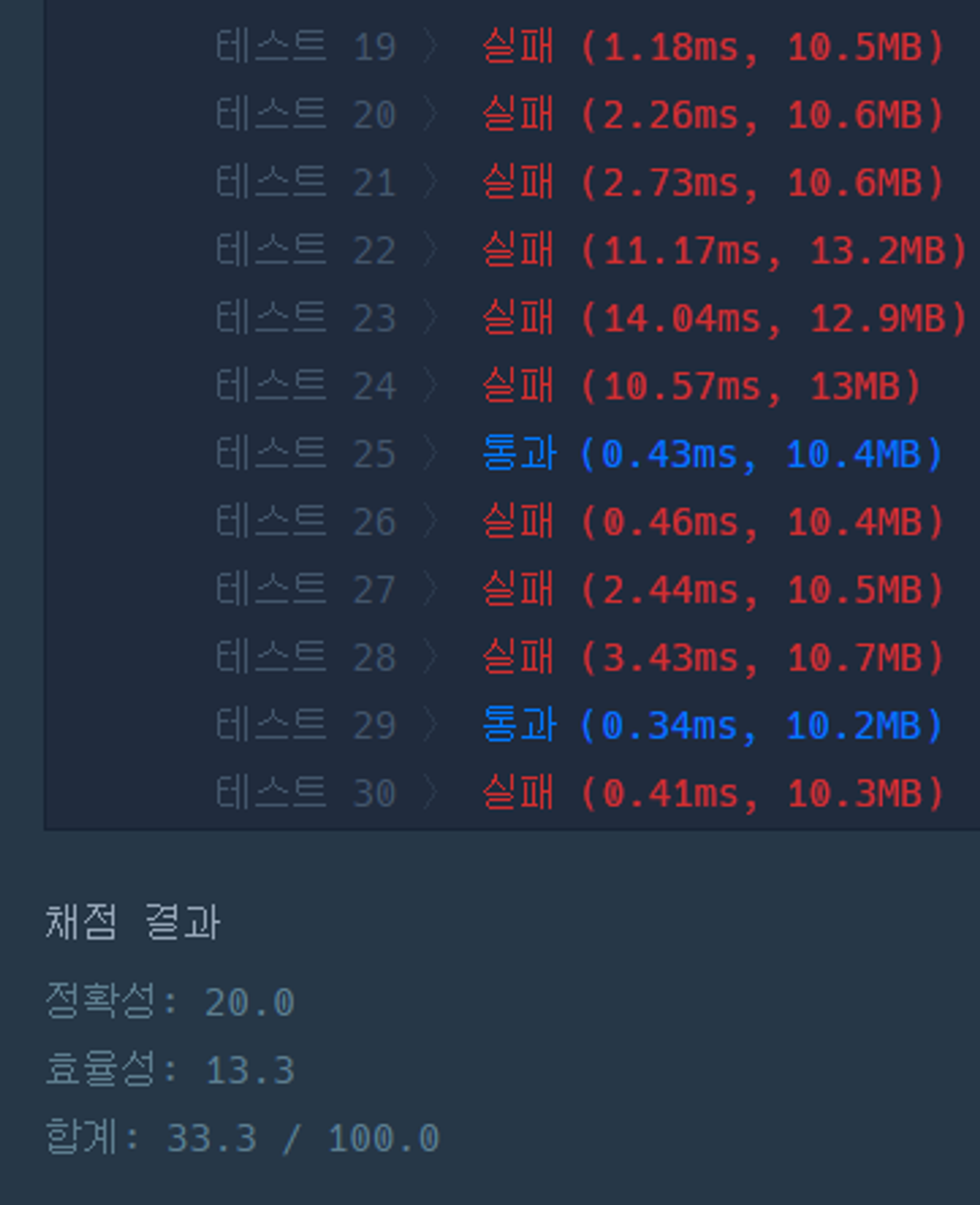
2차 제출(20분 소요)
다익스트라 알고리즘 구현에 있어서 잘못 구현된 부분이 있어 고쳐주었더니 점수는 올랐으나, 올통과하지는 못했다. 코너케이스가 있는듯…ㅠㅠ
import heapq
def solution(n, s, a, b, fares):
path_dict = {}
path_node = []
edges = [[] for _ in range(n+1)]
for c,d,f in fares:
edges[c].append([f,d])
edges[d].append([f,c])
a_to_b_w = [-1 for _ in range(n+1)]
node_w = [-1 for _ in range(n+1)]
min_heap = []
heapq.heappush(min_heap,[0,a,None])
while min_heap:
tw, tn, pn = heapq.heappop(min_heap)
if a_to_b_w[tn] == -1:
a_to_b_w[tn] = tw
if pn != None:
path_dict[tn] = pn
if tn == b:
break
for mw,nn in edges[tn]:
heapq.heappush(min_heap,[tw+mw,nn,tn])
path_node.append(b)
tmp_node = path_dict[b]
while True:
try:
path_node.append(tmp_node)
tmp_node = path_dict[tmp_node]
except:
break
min_heap = []
heapq.heappush(min_heap,[0,s])
while min_heap:
tw, tn = heapq.heappop(min_heap)
if node_w[tn] == -1:
node_w[tn] = tw
for mw,nn in edges[tn]:
heapq.heappush(min_heap,[tw+mw,nn])
min_together_fares = float("inf")
for node in path_node:
min_together_fares = min(min_together_fares,node_w[node])
min_together_fares += a_to_b_w[b]
min_solo_fares = node_w[a] + node_w[b]
# print("path_node: ",path_node)
# print("min_together_fares: ",min_together_fares)
# print("min_solo_fares: ",min_solo_fares)
# print("a_to_b_w[b]: ",a_to_b_w[b])
# print("node_w[a]: ",node_w[a])
# print("node_w[b]: ",node_w[b])
return min(min_together_fares,min_solo_fares)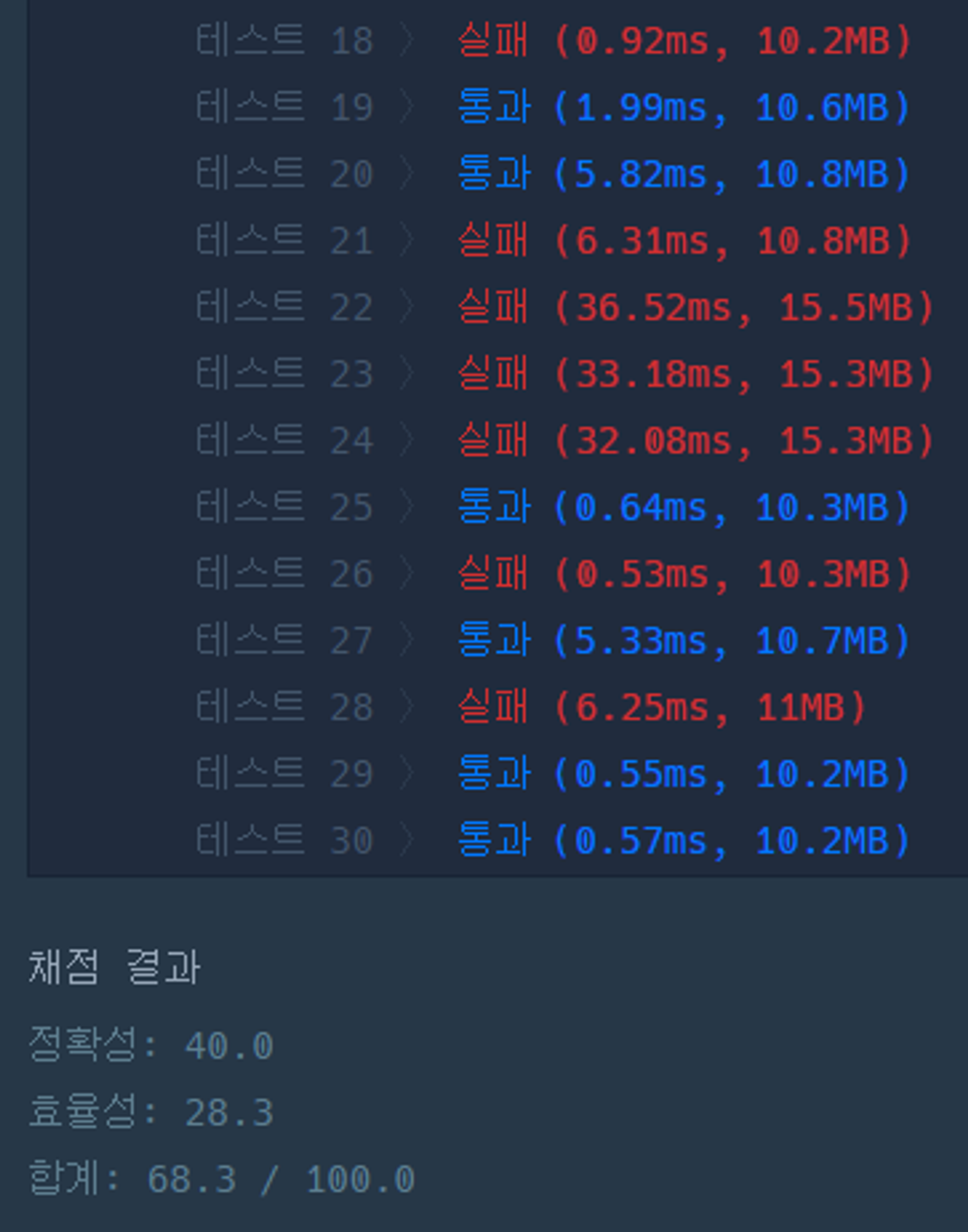
배우게 된 점 [필수 작성]
해설코드 아이디어
이 때 x 지점까지 택시를 합승한다 하면 두 사람의 귀가 경로는 s→x→a, s→x→b가 되며 택시 비용은 cost(s→x) + cost(x→a) + cost(x→b)가 된다. 또한 해당 그래프는 무방향 그래프이기에 cost(x→a) == cost(a→x), cost(x→b) == cost(b→x)가 된다. 즉, s, a, b 3개의 지점에서 x 지점까지 도달하는 최소 비용의 합을 x 지점을 조정해가며 구하면 된다.
→ 반대로(거꾸로) 생각하는 능력!!!
질문 [ 필수 X ]
Q1. 1차 아이디어
제 로직에 문제가 있는것 같은데 반례를 못찾겠습니다.
어떤 경우의 반례가 있을 수 있고,
문제를 풀수 있게 아이디어를 발전시키는 방법이 있을까요?
A1.
예외 테스트 케이스 입니다. 해당 로직은 잘못된 것으로 보이며 min_solo_fares에서 발생 가능한 경로의 중복을 처리해 주지 못하고 있습니다.
n: 6
s: 4
a: 6
b: 2
fares: [[4, 1, 10], [3, 5, 24], [5, 6, 2], [3, 1, 24], [5, 1, 100], [4, 6, 50], [2, 3, 22], [1, 6, 25]]
return: 81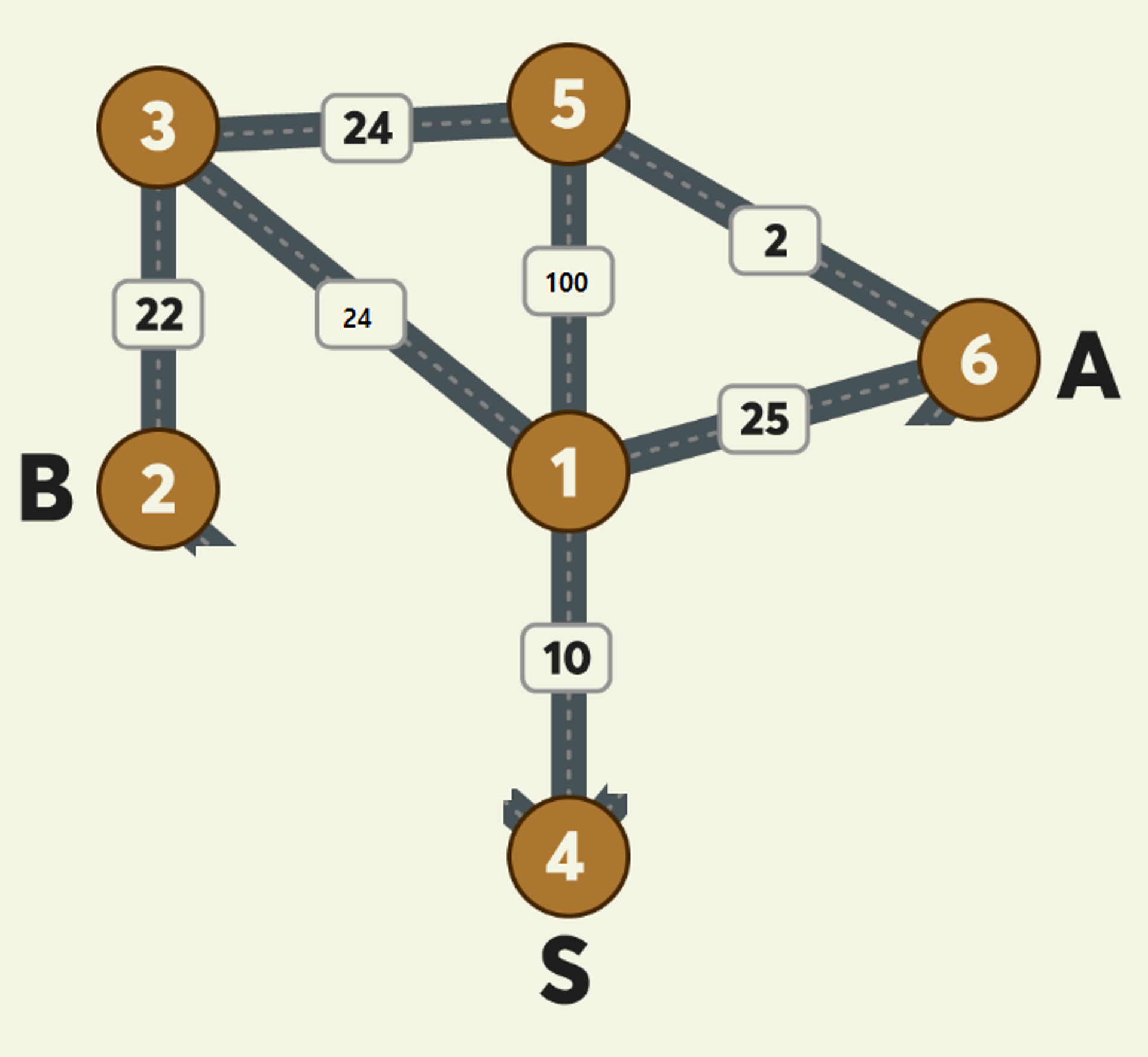
[ 증명하고자 하는 명제 ]
합승하는 경우가 따로 가는 경우보다 더 저렴할때,
합승종료지점은 반드시 A-B 경로상 최단거리경로상에 존재한다.내 로직의 문제는 위 명제가참이 아닌데도, 참으로 가정하고 풀었다는 점이 문제다. 위 명제를 직관적으로 증명하기는 어렵기때문에, 먼저 올바른 로직을 찾는 것이 중요하다. 내가 확신하지 못하는 로직일 경우에는 문제를 최소화해서 반례를 찾아보는 것으로 해당 로직을 검증하는 과정을 거쳐야한다.
