[프로그래머스 Lv.3] 탐욕법(Greedy) - 섬 연결하기

✨ 문제 ✨

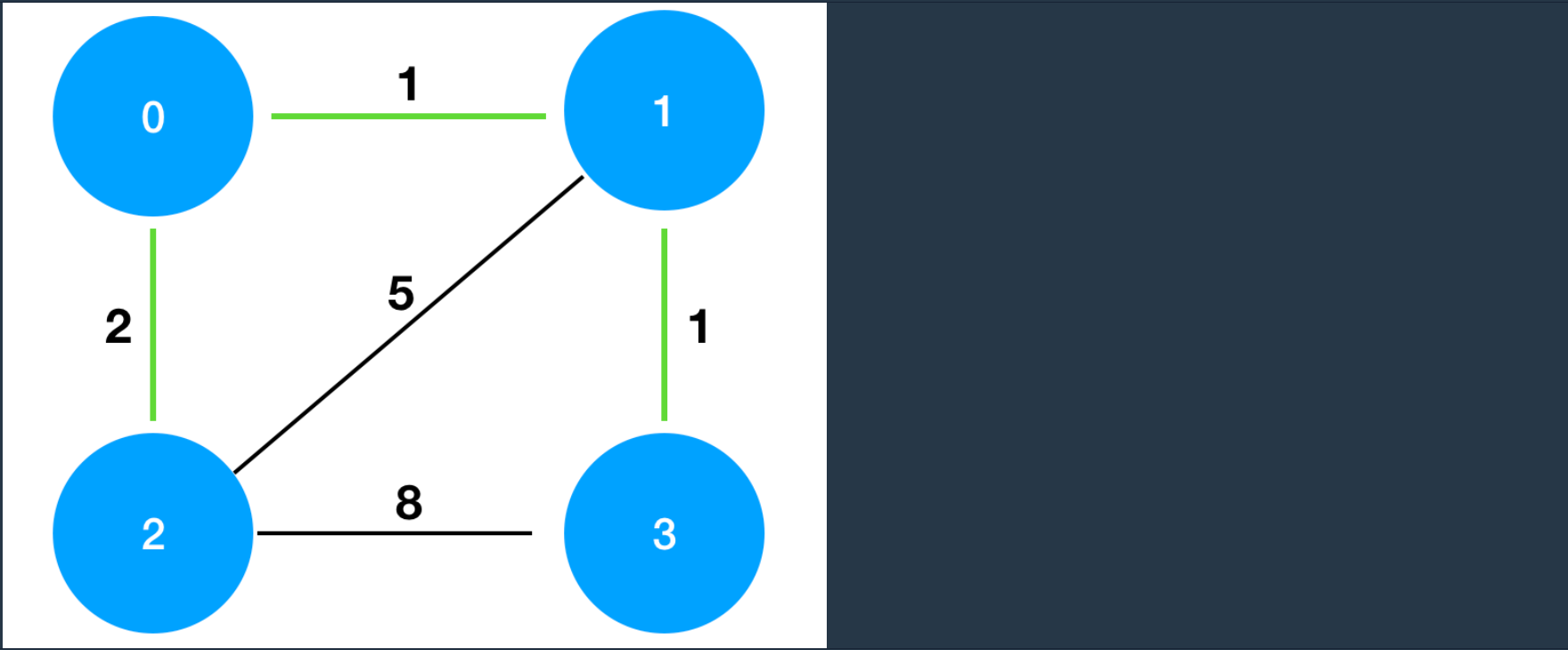
✨ 정답 ✨

function solution(n, costs) {
    let answer = 0;
    const parent = [];
    for(let i=0; i<n; i++) parent.push(i);
    
    costs.sort((a,b)=>a[2]-b[2]);
     
    const getParent = (parent, x) => {
        if(parent[x] === x) return x;
        return parent[x] = getParent(parent,parent[x]);
    }
    
    const unionParent = (parent, x, y) => {
        const n1 = getParent(parent,x);
        const n2 = getParent(parent,y);
        if(n1<n2) return parent[n2] = n1;
        else return parent[n1] = n2;
    }
    
    const findParent = (parent, x, y) => {
        const n1 = getParent(parent,x);
        const n2 = getParent(parent,y);
        if(n1===n2) return true;
        else return false;
    }
    
    for(const cost of costs){
        if(!findParent(parent,cost[0],cost[1])){
            answer += cost[2];
            unionParent(parent,cost[0],cost[1]);
        }
    }
    return answer;
}

🧵 참고한 정답지 🧵

https://velog.io/@jminkyoung/AL-%ED%81%AC%EB%A3%A8%EC%8A%A4%EC%B9%BC-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-feat.-%EC%B5%9C%EC%86%8C-%EC%8B%A0%EC%9E%A5-%ED%8A%B8%EB%A6%AC-JavaScript
https://velog.io/@longroadhome/%ED%94%84%EB%A1%9C%EA%B7%B8%EB%9E%98%EB%A8%B8%EC%8A%A4-LV.3-%EC%84%AC-%EC%97%B0%EA%B2%B0%ED%95%98%EA%B8%B0-JS

💡💡 기억해야 할 점 💡💡

Union-Find 알고리즘: 서로소 집합을 표현할 때 사용하는 알고리즘.

크루스칼 알고리즘: 그리디 알고리즘의 일종. 최소 신장 트리(모든 정점들이 최소한의 간선으로 이어진 트리 중 연결된 간선의 가중치 합이 최소인 트리)를 구하기 위한 알고리즘
👉 그래프들의 간선들의 가중치를 오름차순으로 정렬
👉 사이클을 형성하지 않는 선(Union-Find 알고리즘 사용)에서 순서대로 간선을 선택
👉 선택된 간선을 MST 집합에 추가