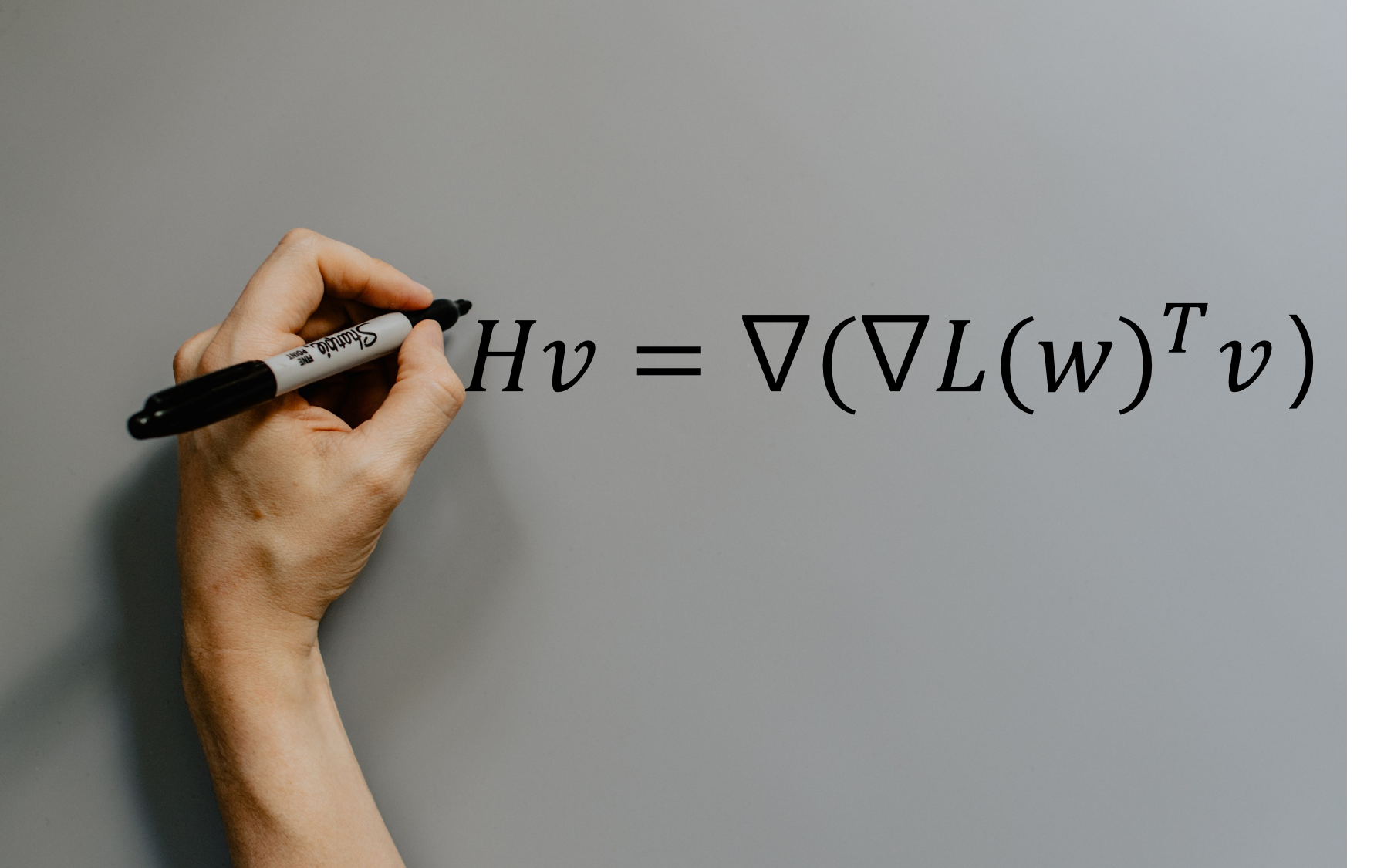Image credit: Kelly Sikkema on Unsplash (modified).

들어가며

뉴럴 네트워크를 최적화할 때 Hessian 행렬 $\mathbf{H}$를 사용하는 경우가 있습니다. (Hessian은 손실함수 $L$에 대해 뉴럴 네트워크 가중치를 이차 미분한 행렬 $\partial^2 L/\partial w_i \partial w_j$을 말합니다.)
저의 경우에도 강화학습 알고리즘 중 하나인 TRPO를 구현하려다 보니 Hessian을 사용해야 하는 상황을 마주쳤습니다.

문제는 뉴럴 네트워크처럼 거대한 모델의 경우 Hessian을 계산해 메모리에 저장해놓는 것이 쉽지 않다는 점입니다. 다행히 대부분의 상황에서 우리는 Hessian 자체가 필요하기보다 Hessian과 특정 벡터 $\mathbf{v}$를 곱한 값 $\mathbf{Hv}$만 구하면 됩니다.

이런 경우에 대해 $\mathbf{Hv}$를 근사 없이 빠르게 계산하는 방법이 있습니다. Pearlmutter가 쓴 "Fast Exact Multiplication by the Hessian"라는 논문에 해당 내용이 나와 있습니다. 본 글에서는 논문에 나온 수식을 정리하고 파이토치로 구현을 해보겠습니다.

Hv를 정확하고 빠르게 계산하는 방법

유도과정을 보기 전에 아래 식을 먼저 감상해보겠습니다.

여기서 $L(\mathbf w)$은 가중치 $\mathbf w$에 따른 손실함수를 나타냅니다.

위 식을 이용하면 $\mathbf H \mathbf v$에 대한 근사값을 구할 수 있습니다. Hessian 행렬 전체를 구할 필요 없이 $L$에 대한 그레디언트를 계산하는 것으로 $\mathbf H \mathbf v$를 구한 것입니다. 하지만 위 식은 근사값을 제공해줄 뿐입니다. 근사에 따른 오차를 줄이고 싶다면 $r$을 작게 만들어야 하는데, $r$이 작아지면 컴퓨터 상에서 수치적으로 정밀도가 떨어질 위험이 있습니다.

아직은 근사적으로 값을 계산한 것에 불과하지만, 최종적인 식까지 한 걸음 밖에 안 남았습니다. 우선은 위 식을 유도하는 방법을 살펴보겠습니다.

$L$을 $\mathbf w$에서 Taylor 전개하면 다음과 같이 됩니다.

위 식을 $\mathbf w$에 대해 미분하겠습니다.

식을 정리하면,

가 됩니다. Hessian에 벡터가 곱해진 꼴로 정리가 되었습니다. 우리는 현재 $\mathbf H \mathbf v$의 값을 구하고 싶은 상황입니다. 그러므로 $\Delta \mathbf w$ 대신에 $r\mathbf v$을 대입해서 정리하겠습니다. $r$은 상수고, $\mathbf v$는 우리가 Hessian에 곱하고자 하는 벡터입니다. 그러면 목표로 하는 다음 식을 구할 수 있습니다.

이제 최종적인 식을 구하는 건 어렵지 않습니다. 마지막 식 양변에 $\lim_{r \rightarrow 0}$을 씌우면 됩니다. 좌변은 $r$이 없으므로 그대로 남습니다. 반면 우변은 $r$로 미분한 것과 같아지게 됩니다.

조금 복잡하지만, 결과적으로는 아래와 같이 다시 쓸 수 있습니다.

그레디언트는 모두 $\mathbf w$에 대한 그레디언트입니다. 우변을 살펴보면, 괄호 안에 있는 식($\nabla L(\mathbf w)^T \mathbf v$)은 스칼라 값입니다. 스칼라 값에 대해 다시 그레디언트를 구하고 있으므로 우변은 결국 벡터가 됩니다.

파이토치를 이용한 구현

간단한 예시를 보겠습니다. 손실함수는 다음과 같이 정의하겠습니다.

여기서 $\mathbf w$는 파라미터고, $\mathbf A$는 대칭 행렬입니다. 이 경우 Hessian 행렬은 $\mathbf A$와 같습니다($\mathbf {H = A}$). 그러므로 $\mathbf{Hv = Av} = \nabla (\nabla L(\mathbf w)^T \mathbf v )$입니다. 정말 이렇게 계산되는지 확인해보겠습니다.

import torch
from torch import nn

torch.manual_seed(0)

A = torch.randn(5, 5)
A = torch.matmul(A, A.T) # A는 대칭 행렬
w = nn.Parameter(torch.randn(5)) # 파라미터
v = torch.randn(5) # Hessian에 곱하고 싶은 벡터

loss = 0.5 * w @ A @ w

w_grad = torch.autograd.grad(loss, w, create_graph=True)[0]
Hv = torch.autograd.grad(torch.dot(w_grad, v), w)[0]

print(Hv)
print(A @ v)

결과를 프린트해보면 아래와 같습니다. 두 가지 방식으로 구한 결과가 같음을 알 수 있습니다(즉 $\mathbf{Av} = \nabla (\nabla L(\mathbf w)^T \mathbf v )$입니다).

# output
tensor([ -8.4135, -12.9879,   8.0082,  21.6127, -23.2350])
tensor([ -8.4135, -12.9879,   8.0082,  21.6127, -23.2350])

참고문헌

Pearlmutter, Barak A. "Fast exact multiplication by the Hessian." Neural computation 6.1 (1994): 147-160.