TRPO 구현을 위해 알야야 할 것들

Hohyun Kim·2022년 7월 25일

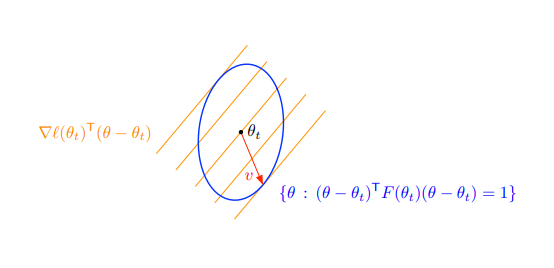
본 포스트는 미완성입니다: 최종 업데이트 2022-08-01

저는 강화학습 알고리즘 TRPO를 구현하기 위해 여러 자료를 찾아보며 공부했습니다. TRPO가 보다 일반적인 최적화 알고리즘과 관련이 있다는 것을 알게 되었고 결과적으로는 많은 것을 배웠습니다. TRPO가 유명한 알고리즘인 만큼 저처럼 TRPO를 구현해보기 위해 자료를 찾아 돌아다니는 분이 있으실 거라 생각합니다. 이에 본 포스트에서 TRPO 구현과 관련하여 알아야 하는 내용을 공유하고자 합니다.

TRPO에서 강화학습과 관련한 요소만 빼면 TRPO를 구현하는 것은 Natural Gradient를 구현하는 것과 다를 바 없습니다. TRPO 논문이 기여한 것은 policy를 안정적으로 학습하기 위한 최종 식을 유도한 부분에 있습니다. 최적화를 하는 구현의 세부 사항은 대부분 Natural Gradient 문헌에 나오는 것이기 때문에 TRPO 논문에서도 Appendix에서 다루고 있습니다. 그러므로 구현 관점에서 TRPO가 궁금하신 분은 Natural Gradient를 알아야 합니다.

들어가기 전에

TRPO에 관한 전체 구현을 보려면 다음 사이트를 비롯해 여러 깃허브를 참고하기 바랍니다. 본 포스트는 이런 코드를 보기 위해 알아야 할 배경지식을 전달하는 것이 목적입니다.

Surrogate Advantage

우선 surrogate advantage를 $\mathcal L(\theta_k, \theta)$ 로 쓰고 다음과 같이 정의하겠습니다.

\mathcal L(\theta_k, \theta) = \underset{s,a \sim \pi_{\theta_k}}{E}{ \frac{\pi_{\theta}(a|s)}{\pi_{\theta_k}(a|s)} A^{\pi_{\theta_k}}(s,a) }

$\pi_{\theta_k}$ 는 $\theta_k$ 를 파라미터로 가진 현재 policy입니다. $A^{\pi_{\theta_k}}$ 는 $\pi_{\theta_k}$ 의 advantage입니다.

$\mathcal L(\theta_k, \theta)$ 은 REINFORCE 같은 다른 policy gradient 알고리즘의 목적함수와 다릅니다. 강화학습은 expected discounted reward를 최대화하는 policy를 만드는 것이 목적이고, 다른 policy gradient 알고리즘은 expected discounted reward를 직접 목적함수로 두기 때문입니다.

J(\theta) = E_{s_0, a_0, ... \sim \pi_\theta} \bigg[\sum_{t=0}^{\infty} \gamma^t r(s_t) \bigg]

반면 TRPO는 surrogate advantage를 목적함수로 둡니다. 그 이유는 $\mathcal L(\theta_k, \theta)$ 이 새로운 policy $\pi_\theta$ 가 현재 policy $\pi_{\theta_k}$ 보다 얼마나 성능이 좋은지를 근사적으로 측정하기 때문입니다.

\mathcal L(\theta_k, \theta) \approx J(\theta) - J(\theta_k)

단 근사가 작동하려면 새로운 policy와 현재 policy의 분포가 너무 차이가 나면 안 됩니다. 그렇기에 surrogate advantage를 목적함수로 이용할 때는 $\pi_\theta$ 가 $\pi_{\theta_k}$ 에서 너무 떨어지지 않도록 제약을 가해야 합니다.

구현 관점에서 보자면 $\pi_{\theta_k}$ 가 모은 샘플들은 buffer에 잠시 저장됩니다. 이 샘플들을 $D_k=\{a, s, ...\}$ 라고 하겠습니다. $D_k$ 를 이용해 $\pi_{\theta_k}$ 를 여러 차례 업데이트를 할 수 있습니다.

$D_k$ 를 이용한 첫 업데이트에서는 rollout policy와 현재 업데이트 하려는 policy가 동일하게 $\pi_{\theta_k}$ 므로, importance weight이 1이 됩니다 ( $\frac{\pi_{\theta}(a|s)}{\pi_{\theta_k}(a|s)} = 1$ ). 이 경우에는 policy gradient와 다를 바 없습니다.

하지만 $D_k$ 를 이용한 두 번째 업데이트에서는 rollout policy와 업데이트를 진행중인 policy가 다르기 때문에 surrogate advantage를 써야 합니다.

Theoretical Update

TRPO는 이론적으로 다음 식에 따라 파라미터를 갱신합니다.

\begin{aligned} \theta_{k+1}= \arg \max_{\theta} \; & {\mathcal L}(\theta_k, \theta) \\ \text{s.t.} \; & \bar{D}_{KL}(\theta || \theta_k) \leq \delta \end{aligned}

제약식에 있는 $\bar{D}_{KL}(\theta || \theta_k)$ 은 현재 policy와 새로운 policy 간의 평균 KL-divergence을 나타냅니다.

\bar{D}_{KL}(\theta || \theta_k) = \underset{s \sim \pi_{\theta}}{E}[ D_{KL}\left(\pi_{\theta}(\cdot|s) || \pi_{\theta_k} (\cdot|s) \right) ]

논문에 따르면 $\delta$ 가 작은 경우 파라미터를 policy 성능의 감소 없이 안정적으로 업데이트할 수 있다고 합니다.

Approximate Update

TRPO의 이론적인 업데이트 식을 봤습니다. 이를 실용적인 알고리즘으로 만들기 위해 다음과 같이 근사합니다.

\begin{aligned} {\mathcal L}(\theta_k, \theta) &\approx g^T (\theta - \theta_k) \\ \bar{D}_{KL}(\theta || \theta_k) & \approx \frac{1}{2} (\theta - \theta_k)^T H (\theta - \theta_k) \end{aligned}

즉 목적함수는 1차식으로 근사하고, 제약식은 2차식으로 근사합니다(각각 Taylor 전개를 1, 2차식까지 한 것입니다). 결과적으로는 다음 업데이트 식을 사용합니다.

\begin{aligned} \theta_{k+1} = \arg \max_{\theta} \; & g^T (\theta - \theta_k) \\ \text{s.t.} \; & \frac{1}{2} (\theta - \theta_k)^T H (\theta - \theta_k) \leq \delta. \end{aligned}

여기서 $g$ 는 목적함수를 한 번 미분한 그레디언트 $\nabla_\theta {\mathcal L}(\theta_k, \theta)$ 를 의미하고, $H$ 는 Hessian matrix로서 $\bar{D}_{KL}(\theta || \theta_k)$ 를 두 번 미분한 값을 $\theta_k$ 에서 평가한 값을 행렬로 나타낸 것입니다. 즉 $H = \nabla_\theta^2\bar{D}_{KL}(\theta || \theta_k) |_{\theta = \theta_k}$ 입니다.

또한 $H$ 는 Fisher information matrix(FIM)와 같습니다. FIM이 무엇인지, 그리고 어째서 KL-divergence가 위와 같이 근사가 되는가는 제가 작성한 다음 글을 참고하기 바랍니다.

https://velog.io/@veglog/Fisher-Information

문헌에 따라 $\theta_k$ 와 $\theta$ 의 순서가 뒤바뀌기도 하는데, 사실은 상관 없기 때문입니다. 즉 다음과 같습니다.

\bar{D}_{KL}(\theta_k || \theta) \approx \frac{1}{2} (\theta - \theta_k)^T H (\theta - \theta_k) \\ \; \\ \bar{D}_{KL}(\theta || \theta_k) \approx \frac{1}{2} (\theta - \theta_k)^T H (\theta - \theta_k) \\

입니다. 두 식에서 $\theta$ 와 $\theta_k$ 의 위치가 달라졌다는 점을 보시기 바랍니다. $H$ 의 경우에도 두 식이 동일합니다.

Natural Gradient

TRPO는 파라미터 업데이트를 다음 식에 따라 합니다.

\begin{aligned} \theta_{k+1} = \arg \max_{\theta} \; & g^T (\theta - \theta_k) \\ \text{s.t.} \; & \frac{1}{2} (\theta - \theta_k)^T H (\theta - \theta_k) \leq \delta. \end{aligned}

Lagrangian duality를 이용하여 위의 최적화 식을 풀어보면 아래와 동일함을 보일 수 있습니다.

\theta_{k+1} = \theta_k + \sqrt{\frac{2 \delta}{g^T H^{-1} g}} H^{-1} g.

위 업데이트 식을 natural gradient update라고 부르겠습니다. TRPO는 여기에 line search를 추가한 것입니다. line search는 뒤에서 다시 얘기하도록 하겠습니다.

(Lagrangian duality는 컨벡스 최적화와 관련한 자료를 참고해주세요)

gradient ascent는 새로운 파라미터가 현재 파라미터에서 너무 멀리 떨어지지 않도록 제약을 둔 채로 목적함수를 일차식으로 근사해 최적화하는 것임을 위에서 설명했습니다. TRPO는 파라미터가 아니라 새로운 policy가 이전 policy와 너무 멀리 떨어지지 않도록 제약을 둡니다. 이는 natural gradient로 볼 수 있습니다.

natural gradient는 파라미터가 아니라 분포에 제약을 두고 최적화 문제를 푸는 것을 말합니다. 더 정확히는 새로운 분포가 KL-divergence 기준으로 현재 분포에서 너무 멀리 떨어지지 않도록 하는 선에서 최적화를 하는 것을 말합니다. policy도 action에 대한 확률분포일 뿐이므로, TRPO의 업데이트 식은 natural gradient와 동일합니다.

natural gradient에 관한 설명은 다음을 참고해주세요.

Matt Johnson’s Natural Gradient Descent and K-Fac Tutorial

Difference Between Gradient Ascent*

어떤 강화학습 알고리즘에서는 목적함수 ${\mathcal L}(\theta_k, \theta)$ 를 최대화하기 위해 gradient ascent를 사용합니다. 여기서는 gradient ascent와 TRPO의 업데이트 식을 비교해보겠습니다.

gradient ascent는 다음과 같이 쓸 수 있습니다.

\theta_{k+1} = \theta_k + \eta g

$\eta$ 는 학습률입니다.

그런데 위 식은 다음과 같은 제약 있는 최적화 문제를 푸는 것과 동일합니다.

\begin{aligned} \theta_{k+1} = \arg \max_{\theta} \; & g^T (\theta - \theta_k) \\ \text{s.t.} \; & \|\theta - \theta_k\|^2 \leq \epsilon. \end{aligned}

위 최적화 식을 Lagrangian duality를 이용하여 풀어보면 학습률 $\eta$ 를 구할 수 있고, 다음처럼 gradient ascent의 업데이트 식과 같게 되는 것을 보실 수 있습니다.

\theta_{k+1} = \theta_k + \sqrt{\frac{\epsilon}{g^Tg}} g

즉 gradient ascent는 파라미터 공간에서 $\theta_k$ 를 중심으로 하는 원형 공간 내에서 최댓값을 찾는 것으로 볼 수 있습니다 (그림 (a)). 반면 TRPO의 업데이트 식은 제약식이 원형이 아니라 타원형으로 생겼습니다 (그림 (b)).

따라서 TRPO가 하는 일은 파라미터 간에 업데이트 가능한 크기의 차이를 두는 것입니다. 어떤 파라미터는 다른 파라미터보다 policy에 미치는 영향이 더 클 수 있기 때문입니다.

그림 출처: Matt Johnson’s Natural Gradient Descent and K-Fac Tutorial

Conjugate Gradient

식을 유도하는 부분은 끝났습니다. 이제 문제는 마지막에 유도된 다음 식을 어떻게 계산할 것인가 하는 점입니다.

\theta_{k+1} = \theta_k + \sqrt{\frac{2 \delta}{g^T H^{-1} g}} H^{-1} g.

가장 큰 문제는 $H^{-1}g$ 입니다. 뉴럴 네트워크처럼 파라미터 수가 많은 모델의 경우 2차 미분 행렬 $H$ 를 메모리에 올려놓을 수도 없고, 역행렬을 구하는 것 역시 계산이 많이 듭니다.

위 계산을 하기 위해 conjugate gradient라는 최적화 기법을 이용합니다. conjugate gradient는 $Ax=b$ 에서 $x$ 를 구하는 문제를 풀기 위해 $A$ 의 역행렬을 구하는 대신 $\frac{1}{2}x^TAx - b^Tx$ 의 최솟값이 되게 하는 $x$ 를 찾습니다. 결과적으로는 $x$ 가 $A^{-1}b$ 일 때 $\frac{1}{2}x^TAx - b^Tx$ 가 최솟값을 가지므로 같은 해를 구할 수 있습니다.

우리 상황에 대입해보면, 우리는 $\frac{1}{2}x^THx - g^Tx$ 의 최솟값을 구하면 되는 것이죠.

본 포스트에서는 conjugate gradient에 대해 자세히 설명하지 않겠습니다. 다만 다음 사항을 지적하겠습니다.

conjugate gradient는 $x$ 의 차원이 $n$ 일 경우 $n$ iteration만에 최적 해에 도달합니다. 하지만 뉴럴 네트워크는 $n$ 의 크기가 너무도 큽니다. TRPO에서는 10 iteration만으로 $H^{-1}g$ 를 근사해도 충분하다고 말합니다.
conjugate gradient가 작동하려면 $H$ 가 positive definite이어야 합니다. 다행히 우리의 $H$ 는 KL-divergence의 2차 미분값인데, 이는 positive semi-definite입니다. $D_{KL}(\theta || \theta_k) \approx \frac{1}{2} (\theta - \theta_k)^T H (\theta - \theta_k)$ 는 $\theta$ 가 무엇이든 $0$ 보다 같거나 크기 때문입니다.
conjugate gradient를 이용하면 $H$ 의 역행렬을 직접 구할 필요는 없지만, $Hx$ 를 계산할 수 있어야 합니다. 문제는 뉴럴 네트워크의 경우 $H$ 도 너무 크다는 점입니다. 따라서 $H$ 를 직접 구하지 않고도 $Hx$ 를 구하는 방법이 필요합니다. TRPO 구현에 따라 $Hx$ 를 구하는 방식에 차이가 있기도 합니다. 이 부분은 다음 섹션에서 다루도록 하겠습니다.

다음은 spinning up RL에서 가져온 구현으로서, numpy를 이용하고 있습니다. (링크)

def cg(Ax, b):
    """
    Conjugate gradient algorithm
    (see https://en.wikipedia.org/wiki/Conjugate_gradient_method)
    """
    x = np.zeros_like(b)
    r = b.copy() # Note: should be 'b - Ax(x)', but for x=0, Ax(x)=0. Change if doing warm start.
    p = r.copy()
    r_dot_old = np.dot(r,r)
    for _ in range(cg_iters):
        z = Ax(p)
        alpha = r_dot_old / (np.dot(p, z) + EPS)
        x += alpha * p
        r -= alpha * z
        r_dot_new = np.dot(r,r)
        p = r + (r_dot_new / r_dot_old) * p
        r_dot_old = r_dot_new
    return x

위 함수의 입력으로 주어지는 Ax는 $Ax$ 값을 계산해주는 function입니다. iterative한 방식으로 $x$ 값을 업데이트 하는데, $x$ 의 initial value는 $0$ 으로 주고 있습니다.

함수의 다른 입력인 b는 목적함수에 대한 뉴럴 네트워크의 gradient가 될 것입니다. 위 함수를 이용하려면 뉴럴 네트워크의 gradient를 하나의 벡터로 합쳐야 합니다. 이를 위해 보통 다른 구현에서도 flat_grad 등의 보조 함수를 정의해놓고 있습니다.

한편 위 구현에서는 Ax 함수에 숨겨져 있지만, 구현상으로는 $Ax$ 대신 $Ax + \beta x$ 를 계산합니다. $\beta$ 는 damping coefficient라고 하며, 0.1이나 0.01 같은 조그만 상수입니다. 이렇게 해주는 이유는 numerical stability 때문입니다. conjugate gradient는 positive definite이어야 작동하기 때문에 $A$ 에 identity matrix를 더해주어 약간 더해주는 것입니다 ( $Ax + \beta x = (A + \beta I)x$ ).

$\beta$ 값이 커지면 정확한 업데이트가 되지는 않지만, 그렇다고 알고리즘 전체에 문제가 생기는 것은 아닙니다. $\beta$ 가 커질수록 gradient ascent와 비슷한 방식으로 업데이트를 하게 됩니다.

conjugate gradient에 대해 궁금하신 분은 다음 자료를 보시기 바랍니다.

An Introduction to the Conjugate Gradient Method Without the Agonizing Pain

Hessian-vector Product

위에서 언급했듯이 conjugate gradient를 이용하려면 $Hx$ 계산을 할 수 있어야 합니다. 코드 상으로는 Ax 함수를 구현해야 합니다. 다행히 Hessian matrix를 직접 구하지 않고도 Hessian matrix에 임의의 벡터 $x$ 를 구하는 계산을 할 수 있습니다. 이와 관련한 설명은 제가 전에 작성한 포스트에 있습니다.

Hessian 없이 Hessian-vector product 구하기

garage의 pytorch 구현은 다음 링크의 _build_hessian_vector_product 함수를 참고해주세요. _build_hessian_vector_product의 리턴 값은 함수입니다. 해당 함수는 conjugate gradient의 서브 루틴으로 이용될 것입니다.

https://github.com/rlworkgroup/garage/blob/master/src/garage/torch/optimizers/conjugate_gradient_optimizer.py

Backtracking Line Search

예를 들어 spinning RL에서는 algo=trpo로 설정시 line search를 수행하고 algo=npg로 설정시 line search를 수행하지 않습니다.
conjugate gradient를 이용하면 $H^{-1}g$ 를 구할 수 있습니다. $v=H^{-1}g$ 로 두면, TRPO의 업데이트 식은 다음과 같습니다.

\theta_{k+1} = \theta_k + \sqrt{\frac{2 \delta}{v^T H v}} v.

"TRPO의 업데이트"라고 부른 것을 TRPO 논문에서는 "natural gradient"라고 부릅니다. TRPO는 여기에 line search를 추가합니다.

\theta_{k+1} = \theta_k + \alpha^j\sqrt{\frac{2 \delta}{v^T H v}} v.

$\alpha$ 는 0.9나 0.8과 같이 0과 1 사이의 상수고, $j$ 는 정수입니다. $j=0$ 일 때는 natural gradient와 같은 식입니다.

line search는 최적의 학습률 $\alpha$ 를 찾는 것을 말합니다. 어떤 경우에는 (conjugate gradient처럼) 문제가 비교적 단순해서 최적의 학습률을 해석적으로 구하는 것이 가능합니다. 우리의 경우에는 그렇게 할 수 없습니다. 대신 다음 방법을 사용합니다.

현재 모델의 파라미터를 복사해 따로 저장해둔다. $j = 0$ 으로 설정한다.
복사해둔 파라미터에 업데이트를 적용한다.
업데이트를 적용한 후 목적함수가 향상되고, (AND) 제약식이 충족되는지 확인한다. 둘 중 하나라도 충족되지 않으면 $j$ 에 1을 더한 후 2번으로 돌아간다.

$j$ 가 커질수록 더 작은 스탭으로 업데이트를 실시하게 됩니다. 이 과정을 정해진 횟수(예를 들어 10번)만큼 반복합니다. 만약 정해진 횟수 후에도 목적함수가 좋아지지 않거나 제약에서 벗어나면, 구현에 따라 그냥 가장 작은 스탭만 취하거나 아예 업데이트를 하지 않기도 합니다.