1. 문제
I. 문제 설명
각 점에 가중치가 부여된 트리가 주어집니다. 당신은 다음 연산을 통하여, 이 트리의 모든 점들의 가중치를 0으로 만들고자 합니다.
- 임의의 연결된 두 점을 골라서 한쪽은 1 증가시키고, 다른 한쪽은 1 감소시킵니다.
하지만, 모든 트리가 위의 행동을 통하여 모든 점들의 가중치를 0으로 만들 수 있는 것은 아닙니다. 당신은 주어진 트리에 대해서 해당 사항이 가능한지 판별하고, 만약 가능하다면 최소한의 행동을 통하여 모든 점들의 가중치를 0으로 만들고자 합니다.
트리의 각 점의 가중치를 의미하는 1차원 정수 배열 a와 트리의 간선 정보를 의미하는 edges가 매개변수로 주어집니다. 주어진 행동을 통해 트리의 모든 점들의 가중치를 0으로 만드는 것이 불가능하다면 -1을, 가능하다면 최소 몇 번만에 가능한지를 찾아 return 하도록 solution 함수를 완성해주세요. (만약 처음부터 트리의 모든 정점의 가중치가 0이라면, 0을 return 해야 합니다.)
II. 제한사항
- a의 길이는 2 이상 300,000 이하입니다.
- a의 모든 수는 각각 -1,000,000 이상 1,000,000 이하입니다.
a[i]는 i번 정점의 가중치를 의미합니다.
- edges의 행의 개수는 (a의 길이 - 1)입니다.
- edges의 각 행은
[u, v]2개의 정수로 이루어져 있으며, 이는 u번 정점과 v번 정점이 간선으로 연결되어 있음을 의미합니다. - edges가 나타내는 그래프는 항상 트리로 주어집니다.
- edges의 각 행은
III. 입출력 예
| a | edges | result |
|---|---|---|
| [-5,0,2,1,2] | [[0,1],[3,4],[2,3],[0,3]] | 9 |
| [0,1,0] | [[0,1],[1,2]] | -1 |
2. 풀이
I. 풀이방법
-
연결된 Node가 가장 적은 Node를 Root Node로 설정한다.(기각)- Tree 구조에선 모든 Node가 Root Node가 될 수 있기 때문에, 편의상 Node[0]을 Root Node라고 가정하자.
-
Root Node로부터 BFS를 사용하여 Leaf Node까지의 경로를 파악한다.
-
경로를 역순으로 탐색하며 (Bottom-up traverse) 자식 Node의 weight를 0으로 만들고, 이를 부모 Node에 더해준다.
-
Root Node의 weight가 0일 경우 연산횟수를 반환하며, 아닐 경우 -1(실패)을 반환한다.
i. 풀이 설명
- 최초의 Tree는 아래와 같다. BFS 경로는
[0,3,1,4,2]라고 가정하자.
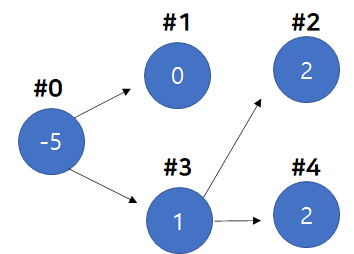
- 우선 2번 Node를 0으로 만들고, 가중치를 부모 Node인 3번 Node에 더해준다.
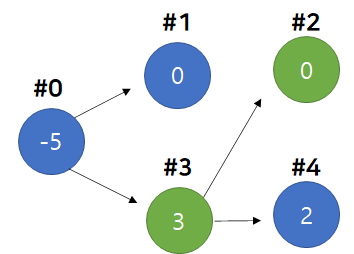
- 4번 Node를 0으로 만들고, 가중치를 부모 Node인 3번 Node에 더해준다.
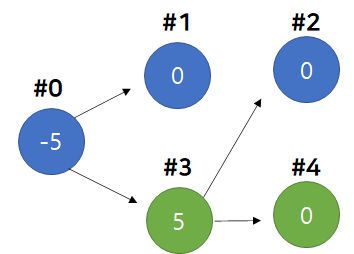
- 1번 Node는 가중치가 0이므로 패스하고, 3번 Node의 가중치를 부모 Node인 0번 Node에 더해준다.
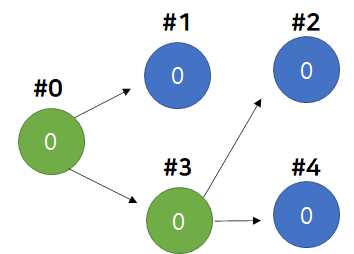
- 최종적으로 Root Node인 0번 Node의 가중치를 확인한다.
II. 소스코드
i. 최초 시도 (시간초과)
- def find_tree()
def find_tree(a, edges):
# 1. 각 Node에 연결된 Node를 Dict로 표현
dic = {}
for edge in edges:
v1 = edge[0]
v2 = edge[1]
if v1 not in dic.keys():
dic[v1] = []
if v2 not in dic.keys():
dic[v2] = []
dic[v1].append(v2)
dic[v2].append(v1)
# 2. 연결된 Node가 가장 작은 Node를 Root Node로 설정.
root_index = min(dic.keys(), key = lambda x : len(dic[x]))
# 3. 설정된 Root를 기반으로 BFS 경로 파악
visited = [False] * len(a)
visited[root_index] = True
visited[dic[root_index][0]] = True
queue = [(root_index, dic[root_index].pop(0))]
path = []
while queue:
parent, child = queue.pop(0)
path.append((parent, child))
for child_ in dic[child]:
if visited[child_] is False:
queue.append((child, child_))
visited[child_] = True
return root_index, path[::-1] #경로를 역순으로 출력- def solution()
def solution(a, edges):
answer = 0
root_index, path = find_tree(a, edges)
# 4. 자식 Node의 가중치를 부모 Node에 더해주면서 Bottom-up Traversal
for parent, child in path:
c_weight = a[child]
answer += abs(c_weight)
a[child] += -1 * c_weight
a[parent] += c_weight
if a[root_index] == 0:
return answer
else:
return -1
return answer
첫 번째 시도는 4개의 문제에서 시간초과가 발생했다.
edges를dict로 만드는 데 문제가 있나 싶어defaultdict를 사용해보았지만 오히려 더 오래 걸리는 경우가 있었다.- Root Node를 찾는 과정은 불필요하기 때문에 이를 제외했지만 역시 실패했다.
구글링 결과, list.pop(0)의 시간복잡도가 O(N)이라는 것을 확인했고, list 대신에 queue를 사용하여 풀어보기로 하였다.
- 그러나
queue를 import하여 사용했을 때,list를 사용했을 때보다 압도적으로 오랜 시간이 걸렸고, 일반적으로deque를queue처럼 사용한다는 사실을 확인하였다.
ii. 두 번째 시도 (성공)
- def find_tree()
from collections import deque
def find_tree(a, edges):
dic = {}
for edge in edges:
v1 = edge[0]
v2 = edge[1]
if v1 not in dic.keys():
dic[v1] = []
if v2 not in dic.keys():
dic[v2] = []
dic[v1].append(v2)
dic[v2].append(v1)
# 바뀐 부분 : list 대신에 dequeue를 사용
q = deque([(-1,0)])
path = []
visited = [0] * len(a)
visited[0] = 1
while q:
p,c = q.popleft()
path.append((p,c))
des = dic[c]
if des:
for d in des:
if not visited[d]:
q.append((c,d))
visited[d] = True
return path[::-1]- def solution()
def solution(a, edges):
answer = 0
path = find_tree(a, edges)
for parent, child in path[:-1]: #맨 마지막은 (-1,0)이므로
c_weight = a[child]
answer += abs(c_weight)
a[child] += -1 * c_weight
a[parent] += c_weight
if a[0] == 0:
return answer
else:
return -1
return answer기존에는 stack, queue, deque를 구현하는 데 있어서 모두 list를 사용하였다. 그러나 element를 추가, 제거하는 데 있어서 list가 비효율적이라는 것을 확인하였고, 효율적인 자료구조형태를 사용하는 것이 좋다는 것을 깨달았다.