🎡 N-Queen
(https://www.acmicpc.net/problem/9663)
시간 제한 메모리 제한 제출 정답 맞힌 사람 정답 비율
10 초 128 MB 55113 27793 18185 49.896%문제
N-Queen 문제는 크기가 N × N인 체스판 위에 퀸 N개를 서로 공격할 수 없게 놓는 문제이다.
N이 주어졌을 때, 퀸을 놓는 방법의 수를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 N이 주어진다. (1 ≤ N < 15)
출력
첫째 줄에 퀸 N개를 서로 공격할 수 없게 놓는 경우의 수를 출력한다.
예제 입력 1
8
예제 출력 1
92
🙄풀이
- 퀸을 체스판 n 번째 행에 둘 수 있는 경우에는 N-Queen 을 만족한 것!
- 퀸을 1번째 행의 i(1~n)번째 열부터 놓으면서 2,3,4 ..., n 번째 행으로 진입 가능 여부를 판단할 것.
- 이때 진입 가능 여부를 판단하는 방법이 중요함.
- 단순히, 퀸이 (x,y) 에 위치할 때 퀸의 공격범위 내에 퀸이 있는지 계속 확인해줘도 되긴 하겠지만 시간이 오래 걸리고 구현하기 번거로울 것으로 예상. (퀸을 한번 놓을때마다 확인절차를 계속 걸쳐야 하므로)
퀸을 (row,col) 에 놓았을 때 확인해야 할 점
- A: 퀸과 같은 열에 새로운 퀸을 둘 수 없음.
-> bool isused_col[]- B: 퀸을 포함하는 우상향 대각선 라인에 새로운 퀸을 둘 수 없음.
-> bool isused_Increasing_Diagonal[]- C: 퀸을 포함하는 좌하향 대각선 라인에 새로운 퀸을 둘 수 없음.
-> bool isused_Decreasing_Diagonal[]
(변수 네이밍이 마음에 안들긴 하지만...)
- 퀸을 (0,0) ~ (0,n) 에 놓으면서 A, B, C 를 확인하며 새로운 퀸을 (1,0)~ (1,n) 에 놓을 수 있는지 확인함.
- 이 과정을 걸쳐 결국 n 행에 퀸을 놓을 수 있다면 count ++
근데, A,B,C indexing 을 어떻게 해야할까?
만약 (x,y) 에 퀸이 위치한다고 가정하자.
-
A: 퀸과 같은 열에 새로운 퀸을 둘 수 없음.
-> bool isused_col[]
조건 같은 경우에는 그냥 isused_col[y] 를 확인해주면 된다. -
B: 퀸을 포함하는 우상향 대각선 라인에 새로운 퀸을 둘 수 없음.
-> bool isused_Increasing_Diagonal[]
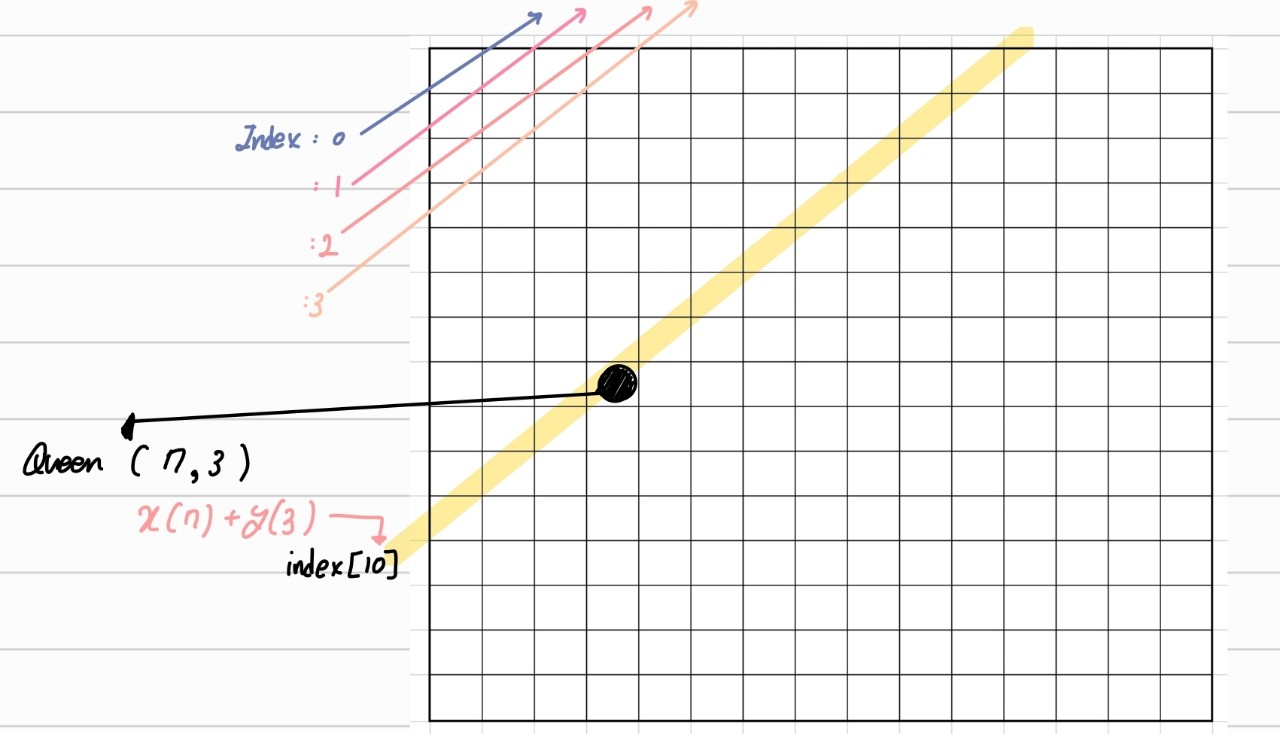
위 그림과 같이 0행 0열을 지나가는 우상향 대각선의 index를 0이라고 하고, 이 대각선을 기준으로 한 칸씩 내려오는 대각선의 index 를 1,2,3 ... 이라고 하면 된다.
이렇게 정한 경우에는 퀸이 (x,y) 에 위치한다면 isused_Increasing_Diagonal[x+y] 를 모조리 true 로 해주면 될 것. -
C: 퀸을 포함하는 좌하향 대각선 라인에 새로운 퀸을 둘 수 없음.
-> bool isused_Decreasing_Diagonal[]
이 경우도 똑같지만 살짝 귀찮을 수 있다.
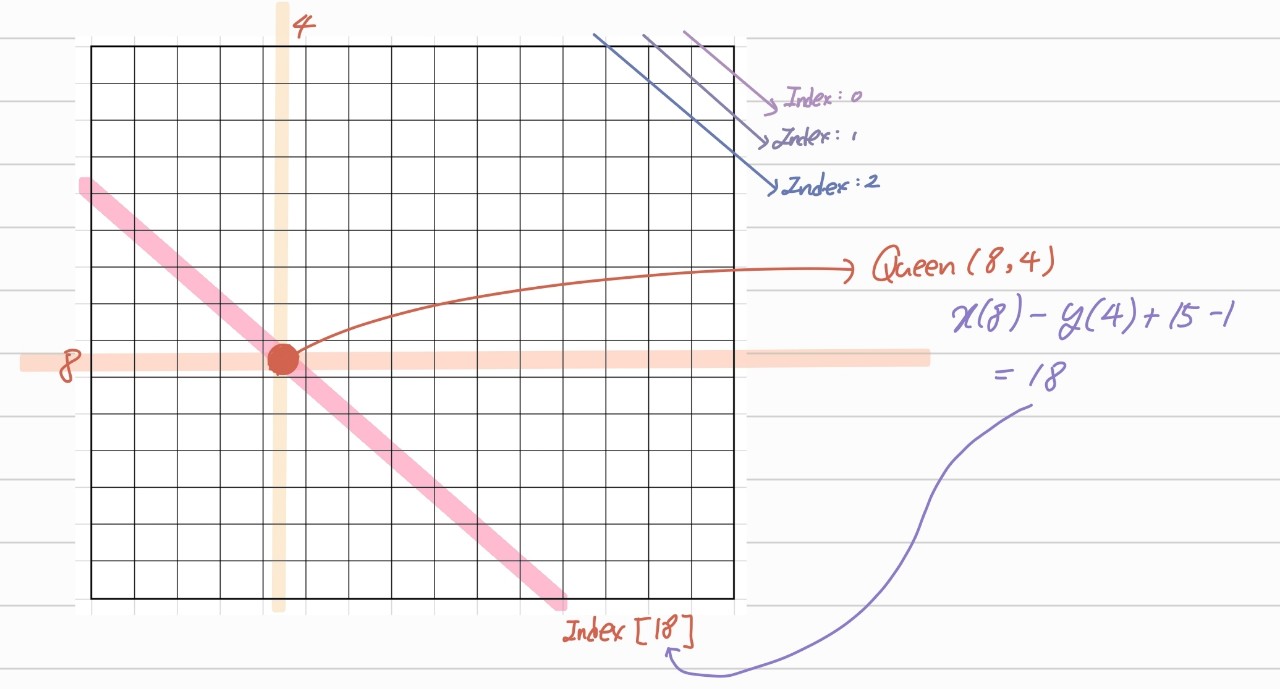
0행 15열을 지나는 대각선의 index 를 0이라고 하고, 한 칸씩 내려오는 대각선의 index 를 1,2,3 ... 이라고 하였다.
이렇게 정한 경우에는 만약 퀸이 (x,y) 에 위치한다면 true 처리해야 하는 index 는 x-y+n-1 로 하면 된다.
( 왜 -1을 해주었냐면, index를 0에서부터 시작하게 하기 위함이다.)
isused_Decreasing_Diagonal[x-y+n-1]
코드
/*
BOJ : https://www.acmicpc.net/problem/9663
backtracking N-Queen
Versatile0010
*/
#include <bits/stdc++.h>
using namespace std;
int n;
int cnt = 0;
bool isused_col[30];
bool isused_Increasing_diagonal[30];
bool isused_Decreasing_diagonal[30];
void func(int cur) // cur 번째 행에 퀸을 배치함
{
if (cur == n)
{
cnt++;
return;
}
for (int i = 0; i < n; i++) // cur 행 i 열을 순회
{
if (isused_col[i] || isused_Increasing_diagonal[cur+i] || isused_Decreasing_diagonal[cur-i+n-1])
continue; // 퀸을 놓을 수 없는 경우
else // 퀸을 놓을 수 있는 경우
{
isused_col[i] = true; // 해당 칸 세로에 true
isused_Increasing_diagonal[cur + i] = true; //해당 칸 우상향 대각선에 true
isused_Decreasing_diagonal[cur - i + n - 1] = true; //해당 칸 좌하향 대각선에 true 처리
func(cur + 1);
isused_col[i] = false;
isused_Increasing_diagonal[cur + i] = false;
isused_Decreasing_diagonal[cur - i + n - 1] = false;
}
}
}
int main()
{
ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
cin >> n;
func(0);
cout << cnt;
return 0;
}GIT : https://github.com/versatile0010/PS/blob/main/Backtracking/BOJ%209663.cpp
