Optimization
Gradient Descent
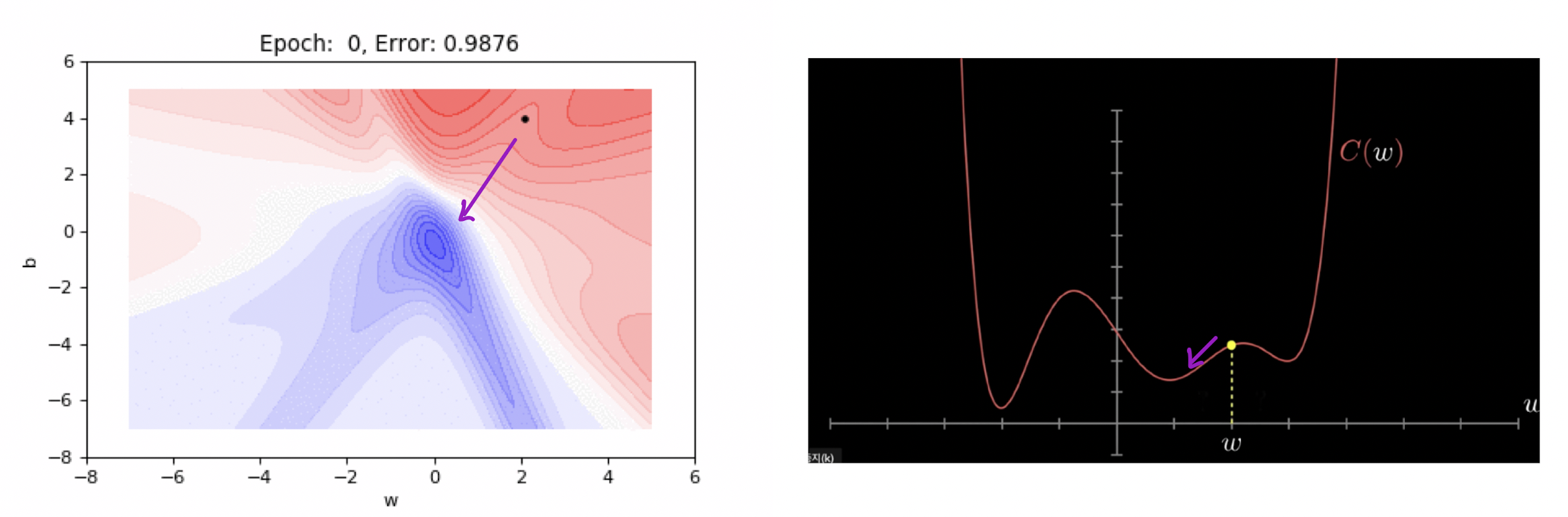 경사하강법의 첫번째 목적은 미분가능한 함수에서의 "지역 최소값"을 찾는것이다.
경사하강법의 첫번째 목적은 미분가능한 함수에서의 "지역 최소값"을 찾는것이다.
Optimization Concepts
Generalization
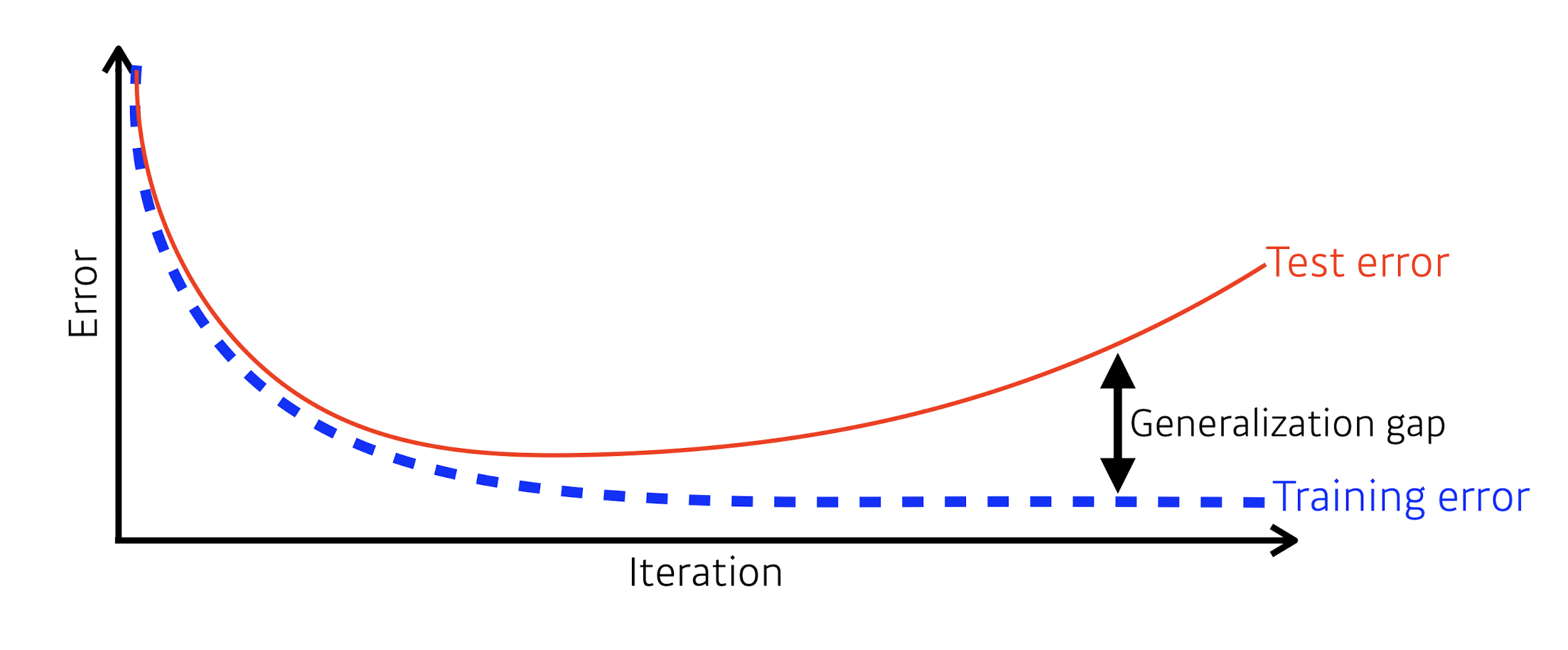
모델을 어떻게 일반화시킬것인가? = 모델이 새로운 데이터에 대해 얼마나 잘 훈련되어 있는가?
= generalization gap 을 어떻게 줄일 것인가?
Underfitting VS Overfitting
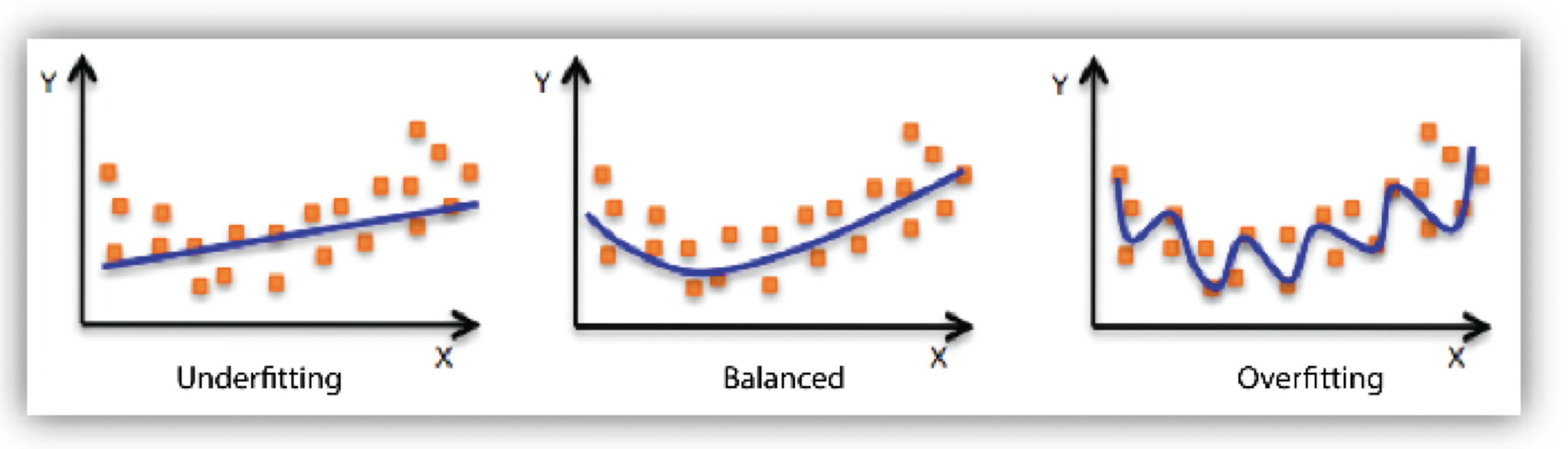
학습데이터에도 맞지않는(underfitting) VS 실제 데이터에 맞지않는(overfitting)
Cross Validation
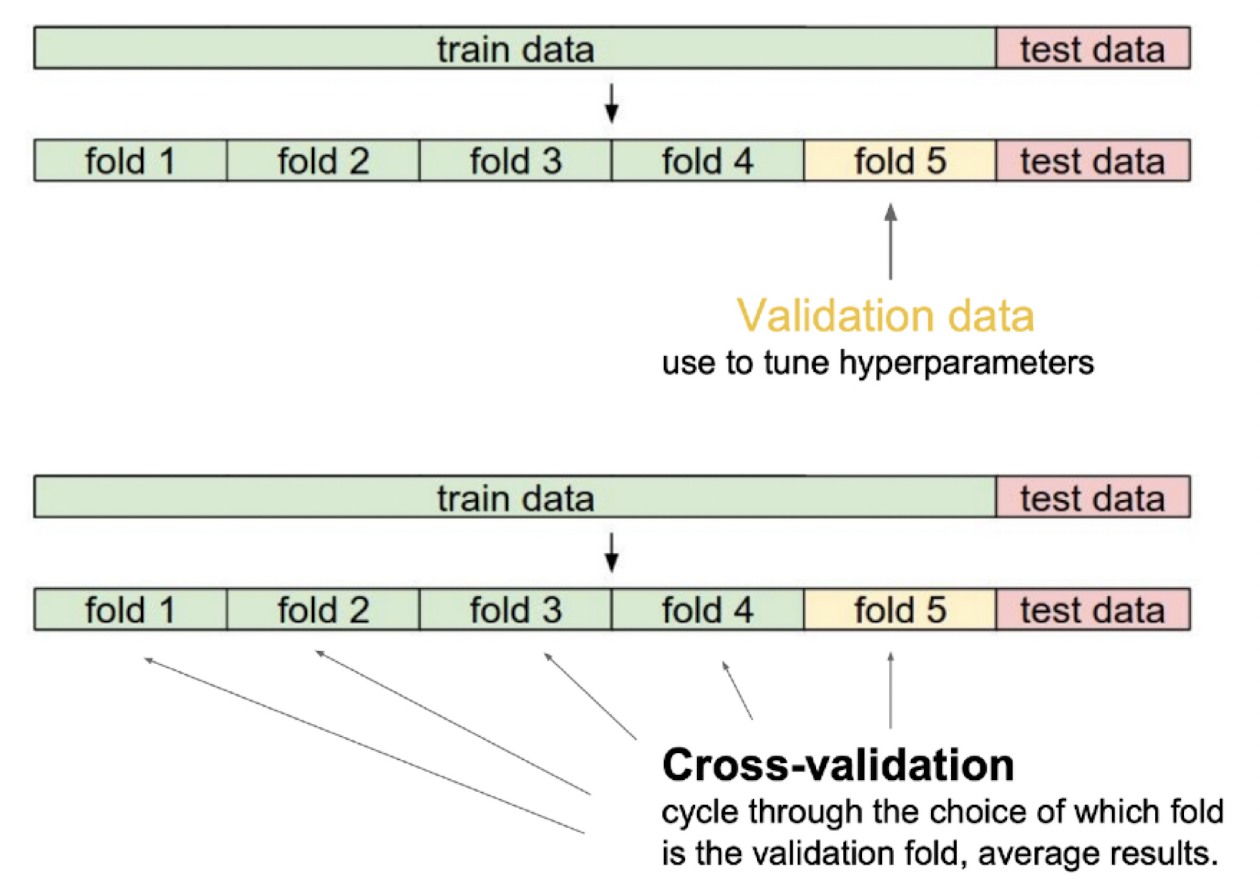
Cross-validation is a model validation technique for assessing how the model will generalize to an independent (test) data set.
안그래도 적은 train data을 train / val으로 나누면 더 작아지므로 이러한 데이터의 부족을 해결하고자 나온 컨셉인 교차검증 방법이다. K겹 교차검증(K-fold Cross Validation)이란 train을 K개로 나누어 K개의 모델을 만드는것을 말한다.
( train : [1,2,3,4], val : [5] -> train : [1,2,3,5], val : [4] -> ...)
이렇게 만들어진 K개의 모델을 합치면 하나의 val셋으로만 훈련시킨 모델보다는 더 Generalization 된 모델이 나오게 된다.
Bias and Variance
편향은 학습 알고리즘에서 잘못된 가정을 했을 때 발생하는 오차이다. 높은 편향값은 알고리즘이 데이터의 특징과 결과물과의 적절한 관계를 놓치게 만드는 과소적합(underfitting) 문제를 발생 시킨다.
분산은 트레이닝 셋에 내재된 작은 변동(fluctuation) 때문에 발생하는 오차이다. 높은 분산값은 큰 노이즈까지 모델링에 포함시키는 과적합(overfitting) 문제를 발생 시킨다.
(여기서 오차는 Test데이터셋과의 오류를 말하는것이다)
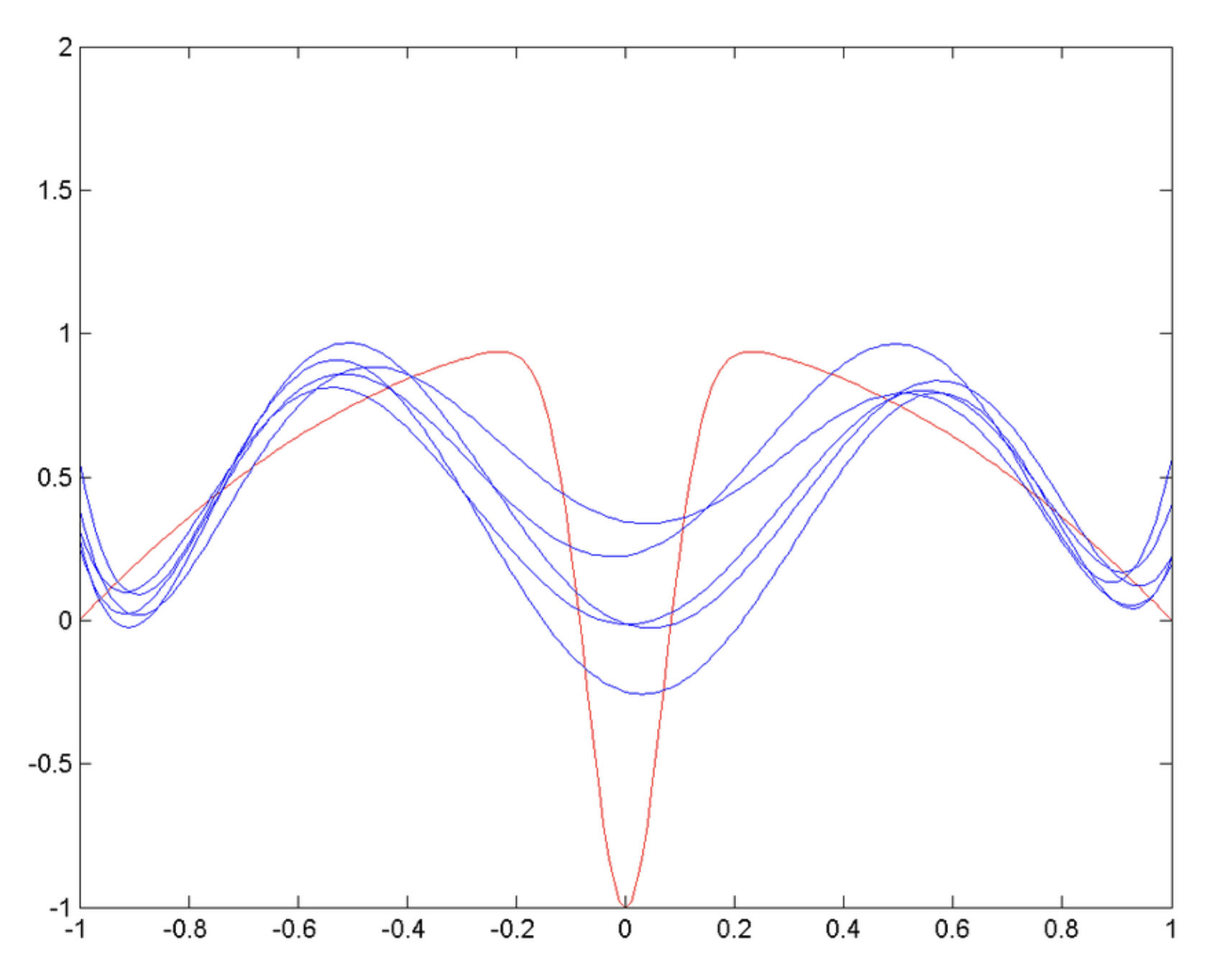
bias(편향) : 모델이 트레이닝되어있지 않으면 편향이 높다 -> 모델이 처음 초기화되어있을 경우 모델은 틀린 가정을 가지고 있기 때문에 고편향(정답과의 오차가 큼) 되어있다.
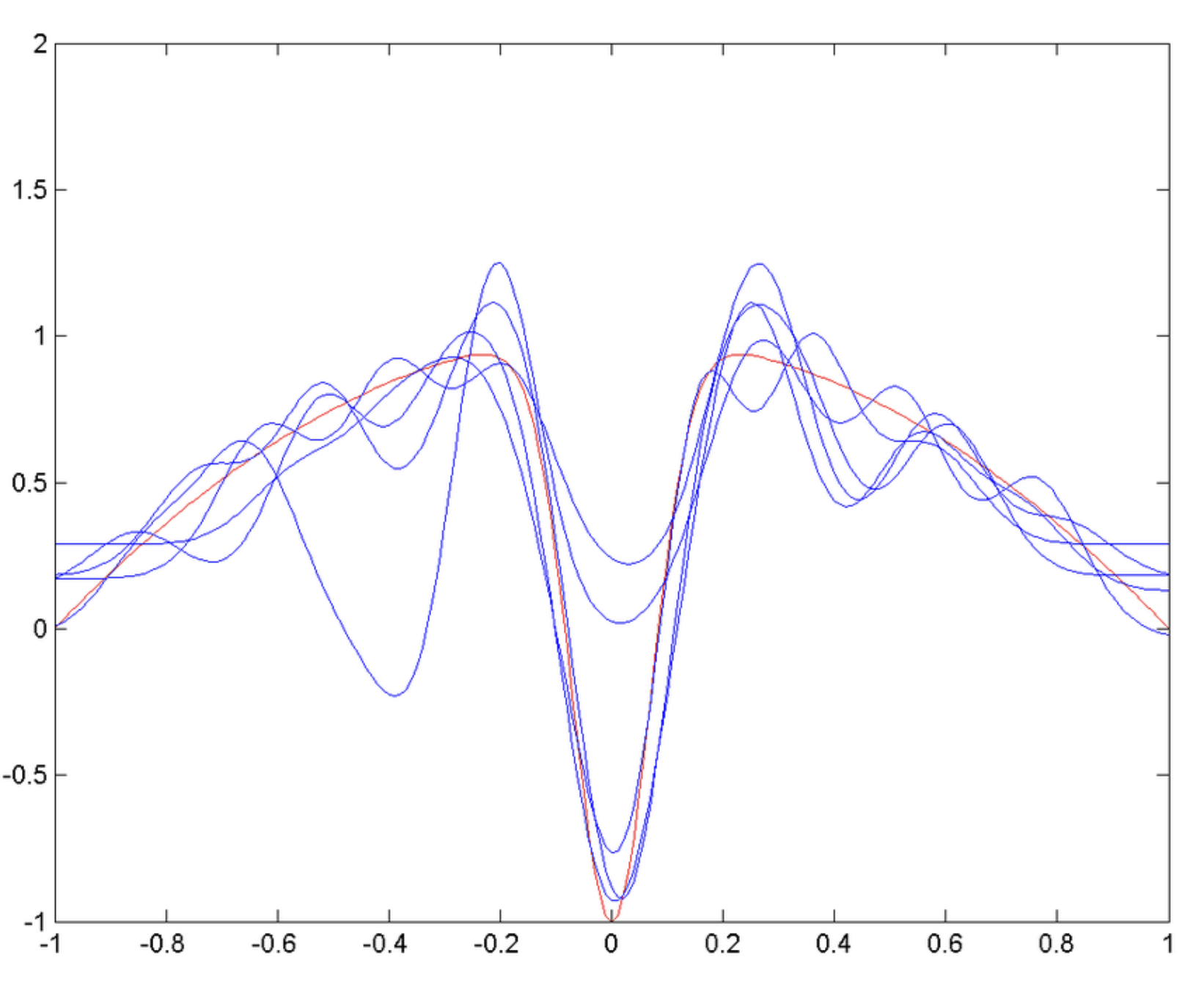
variance(분산) : 모델이 오버트레이닝 되어있으면 분산이 높다 -> 모델이 오버트레이닝되면 트레이닝데이터의 노이즈까지 훈련하기 때문에 고분산(정답과의 오차가 큼) 되어있다.
편향과 분산은 서로 트레이드오프 관계에 있다 = 낮은 편향과 낮은 분산을 동시에 가지는것은 불가능하다 = 높은 편향과 높은 분산을 동시에 가지는것도 불가능하다
Bias and Variance Tradoff
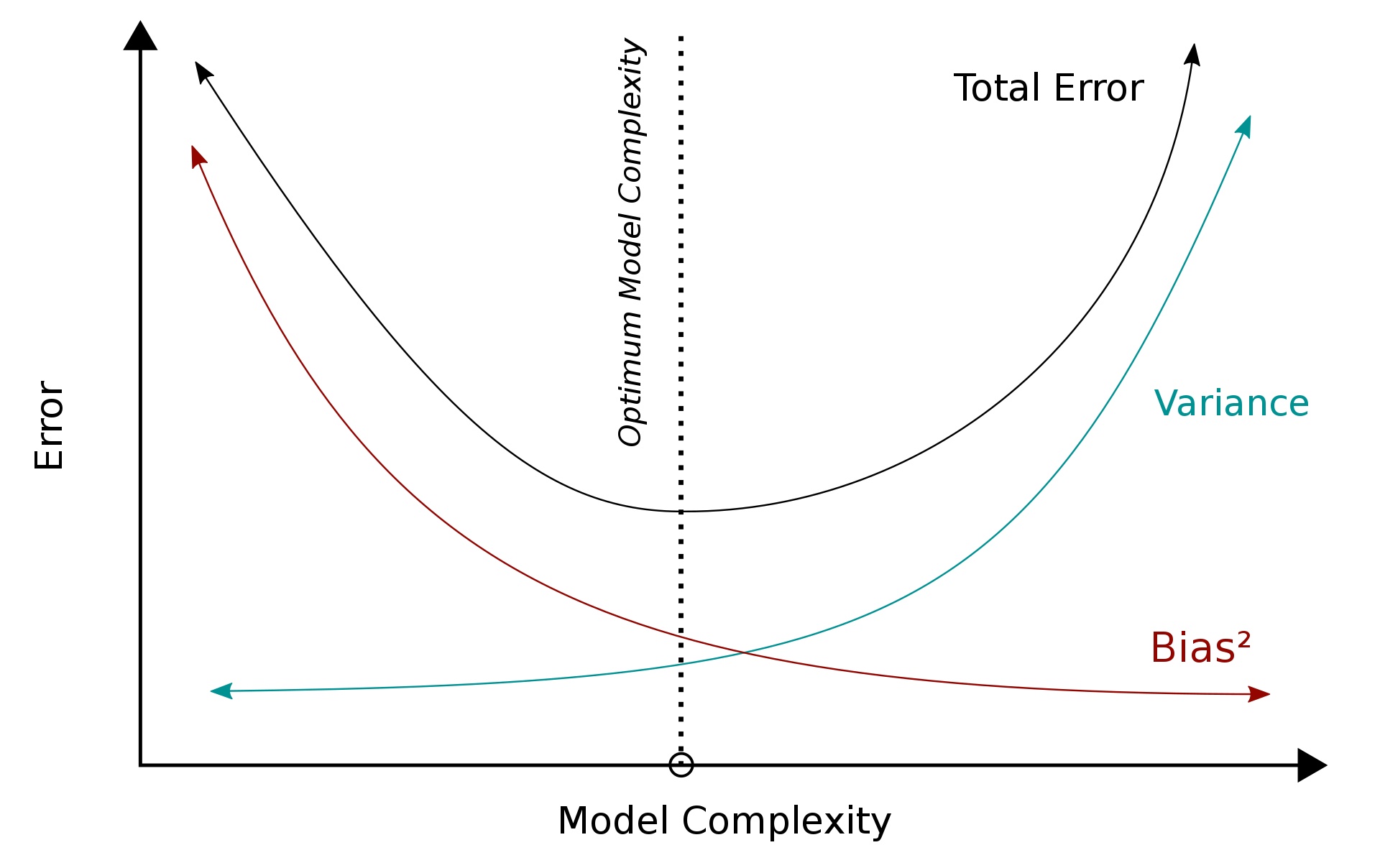 여기서 그림의 Error는 테스트 데이터셋에서 발생하는 Error이다.
여기서 그림의 Error는 테스트 데이터셋에서 발생하는 Error이다.
편향-분산 트레이드오프는 지도 학습에서 매우 중요한 문제이다. 모델을 선택할 때(model selection), 트레이닝 데이터의 규칙을 정확하게 포착하는 것 뿐만이 아니라, 보이지 않는 범위에 대해서 일반화(generalization)까지 하는 것이 이상적이다. 하지만 안타깝게도 이 둘을 동시에 완전히 성취하는것은 사실상 불가능하다. 고분산 학습 알고리즘은 트레이닝 셋을 잘 표현하기는 하지만, 지나치게 큰 노이즈나 아예 부적절한 트레이닝 데이터까지 과적합(overfitting)할 위험이 있다. 반대로 고편향 학습 알고리즘은 과적합(overfitting) 문제가 거의 없는 단순한 모델을 제시하지만 트레이닝 데이터로부터 중요한 규칙성을 제대로 포착하지 못하는 과소적합(underfitting) 문제가 발생한다.
편향값이 낮은 모델은 일반적으로 더 복잡하기 때문에(예: 더 높은 차수의 회귀 다항식) 트레이닝 셋을 더 정확히 표현한다. 하지만 모델링 과정에서 커다란 노이즈 성분까지 반영할 가능성이 있고, 그런 경우에는 더 복잡함에도 불구하고 덜 정확한 추론을 하게 된다. 반대로 편향값이 높은 모델의 경우 간단한(낮은 차수의 회귀 다항식) 경향이 있는데, 트레이닝 셋의 데이터를 모델에 충분히 포함하지 못해 분산값이 낮게 나올 수가 있다.
Bagging VS Boosting
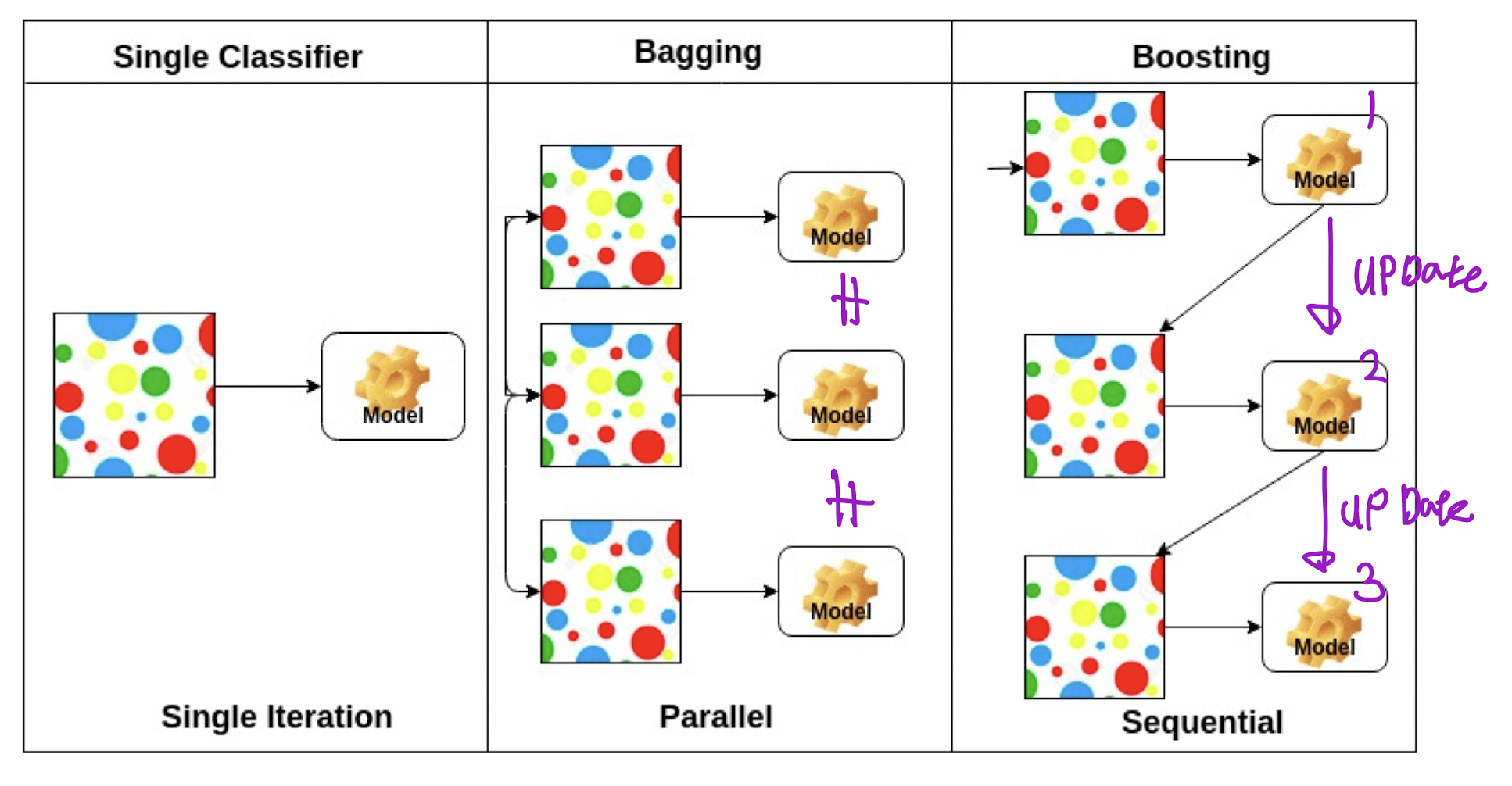
Bagging
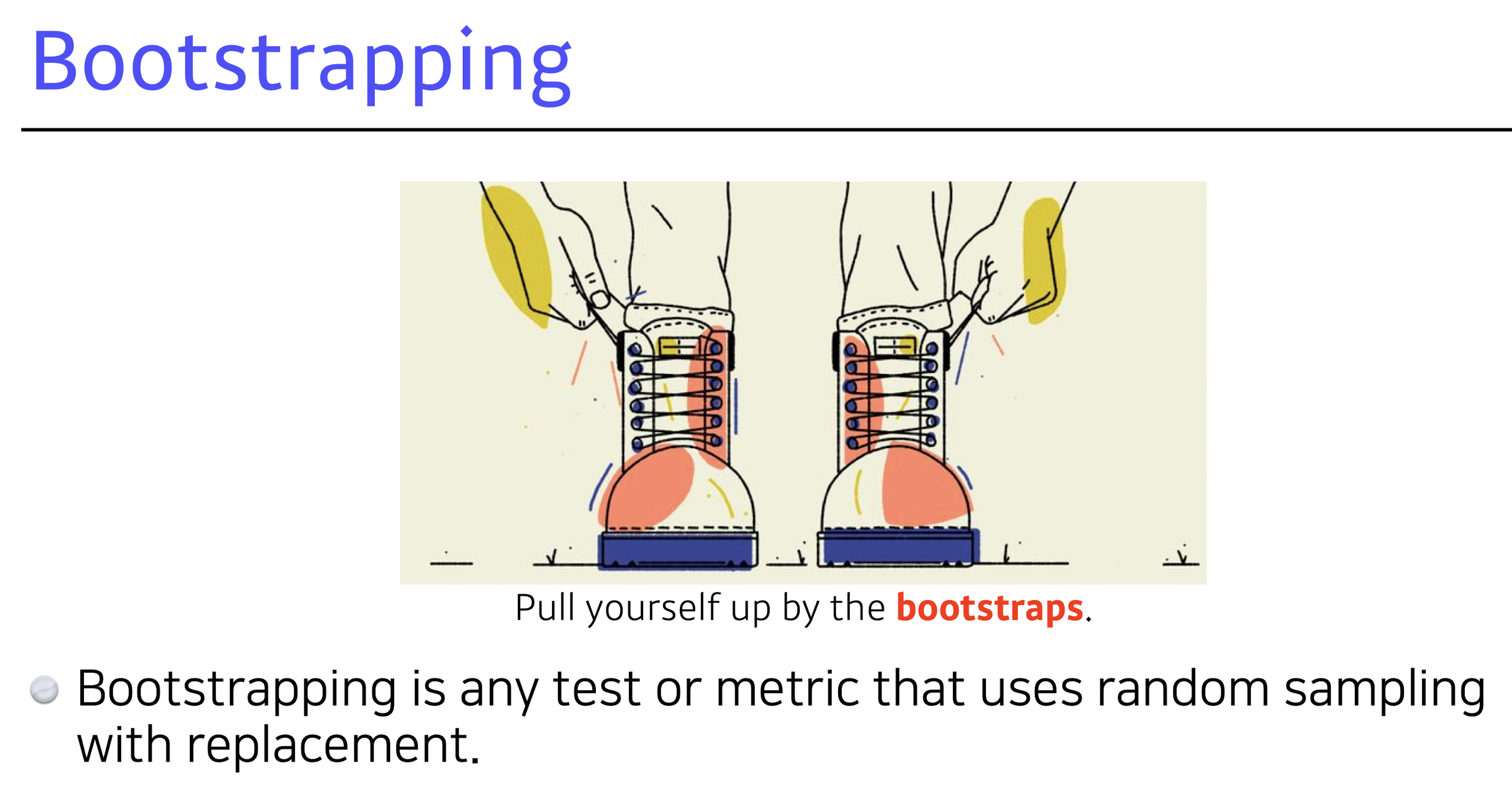
Bootstrapping : 고정된 학습데이터에서 subsampling을 통하여 만든 다수의 모델을 사용하여 더 좋은 성능의 모델을 만들겠다.

Bagging : Bootstrapping을 통해 만들어진 여러 예측 모델을 결합하여 최종 예측 모델을 만드는것 -> 예측모델의 분산을 줄여주므로 고분산된 모델에 적용하는것이 적합함 (목표 변수가 연속형일 경우에는 평균을 목표 변수가 범주형일 경우에는 투표를 사용합니다)
Boosting

Boosting : 기존의 분류모델에서 잘못 분류된 개체들의 가중치를 높히고 제대로 분류된 개체들의 가중치를 낮춤으로써 분류모델을 업데이트하고 또다시 오분류된 개체의 가중치를 높히고 정분류된 가중치를 낮추는 형식으로 모델을 업데이트 해가는 것
Gradient Desent Methods
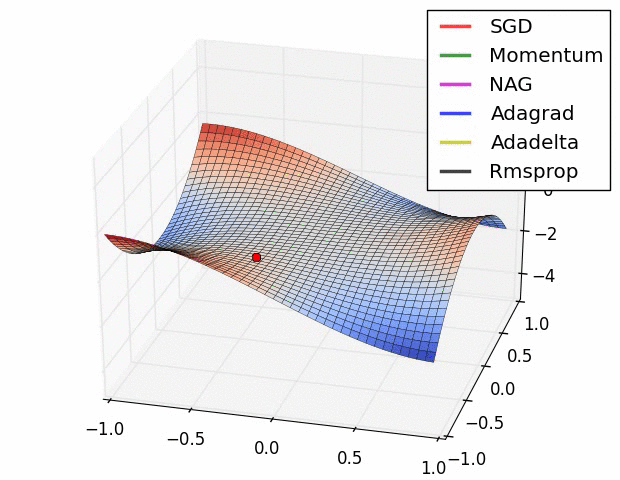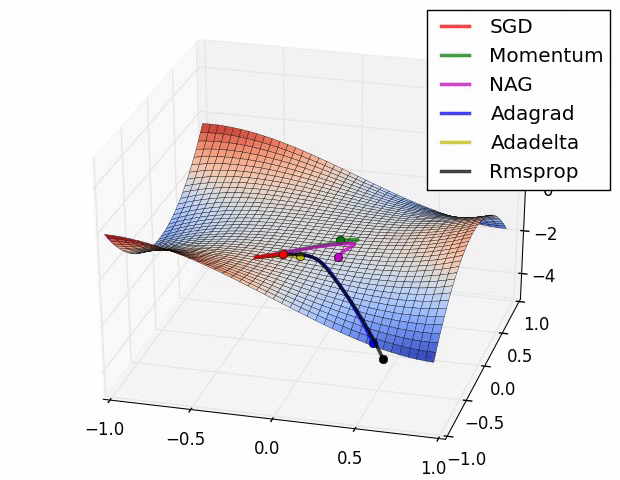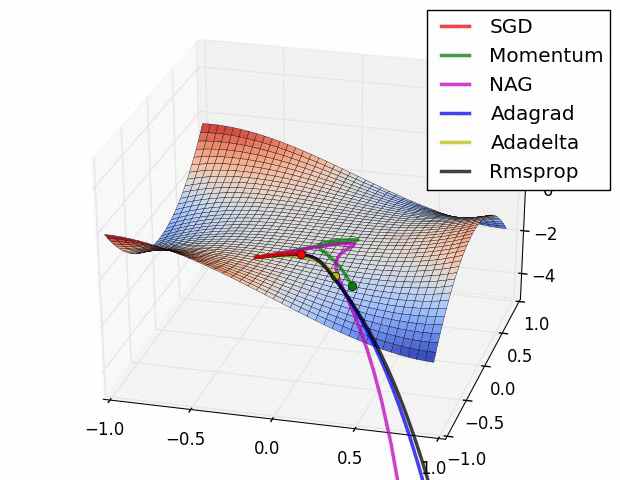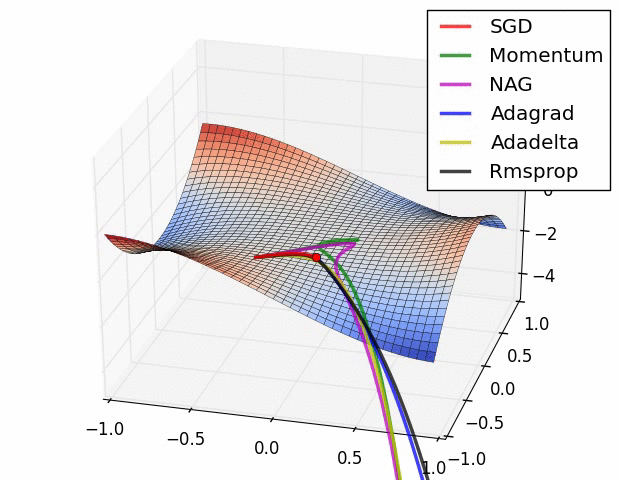
경사하강법의 방법론
Stochastic gradient descent
하나의 데이터셋 샘플에서 경사하강법을 시행합니다.
Mini-batch gradient descent
여러 데이터셋 샘플을 만들어 동시에 경사하강법을 시행합니다.
Batch gradient descent
전체 데이터셋에서 경사하강법을 시행합니다.
Batch-size Matters
큰 배치 사이즈는 트레이닝 모델과 테스팅 모델에서 날카로운 최적점을 만든다.
작은 배치 사이즈는 지역적 최적점을 만든다.
