이번 포스트에서는 Supervised Learning 기법 중 하나인 SVM(Support Vector Machine)에 대해서 다룹니다.
Background
어떠한 데이터들이 주어졌을 때 특성 및 분포를 파악하여 분류를 하는 것은 매우 중요한 Task이다. 분류를 어떤 수식과 방식으로 하는지에 따라 분류 모델의 성능이 결정된다. 분류를 할 때 데이터에 특성 및 분포에 따라 기준이 만들어진다. 이것을 decision boundary라고 부른다. decision boundary를 보며 분류 모델의 성능을 파악할 수 있다. 이번 포스트에서 다룰 SVM(Support Vector Machine)은 이 decision boundry를 구할 모델이다.
SVM
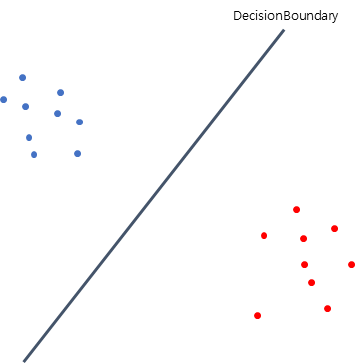
SVM은 decision boundary를 구하기 위한 기법이다. 다음의 그림에서 어떤 decision boundary가 좋을지 생각해 보자.
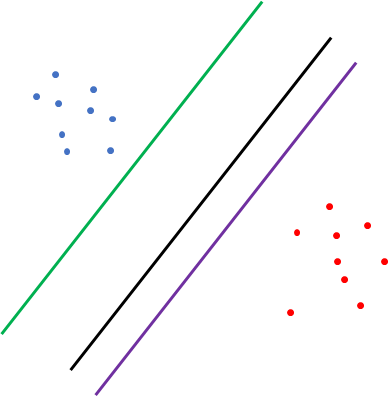
먼저 초록색 decision boundary를 보게 되면 분류는 잘 됐지만 파란색의 class에 너무 가깝다. 보라색 decision boundary도 마찬가지로 분류는 잘 됐지만 빨간색의 class에 가깝게 위치했기 때문에 분류 성능에 문제가 있을 수 있다. 마지막으로 검은색 decision boundary를 보면, 각 class를 잘 분류하기도 했으며, 거리가 일정하게 멀기 때문에 좀 더 Robust(강건한)하며 분류의 성능도 좀 더 확고하다. 아슬아슬하게 분류하는 모델보단 안전하면서 확실하게 분류하는 모델이 좀 더 좋은 성능의 모델이라고 볼 수 있다.
그렇다면 검은색 decision boundary와 같이 각 class와의 거리가 가장 멀게 분류하려면 어떻게 해야 할까? 정답은 각 class와의 margin이다. 위에서 언급했듯이 각 class와의 margin이 최대화되는 지점을 decision boundary로 사용한다.
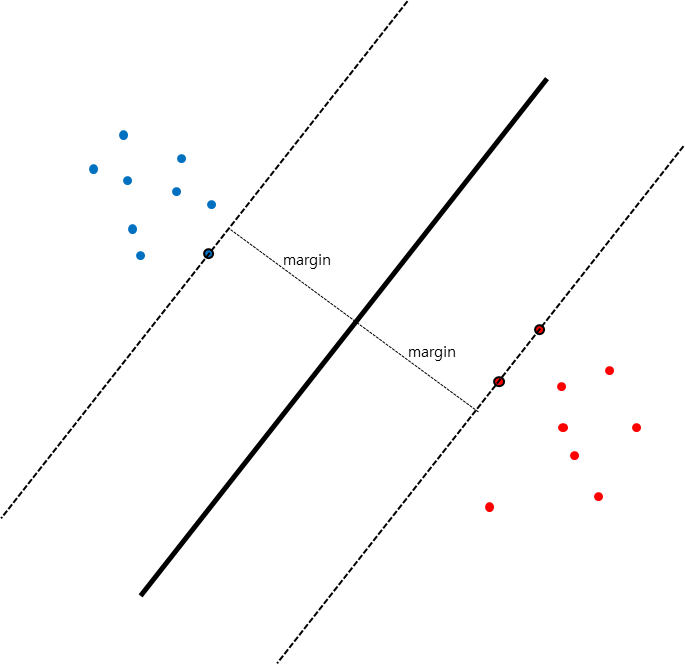
여기서 margin 연산을 할 때 사용하는 기준은 위 그림에서는 3개의 데이터가 있는데, 이를 Support Vector라고 부르며 전체 데이터를 사용하며 학습하지 않고 Support Vector들로만 학습하기 때문에 연산량이 매우 절약된다. 위의 특성 때문에 Support Vector Machine이라고 불린다.
Outlier 처리
데이터의 통계가 위에서 보았던 그림처럼 이쁘게 나누어져 있다면 모델을 결정지을 때 매우 쉬울 것이다. 하지만 실제 데이터의 분포는 저런 형태보다는 outlier가 포함돼있는 경우가 대부분이다. 다음의 그림을 봐보자.
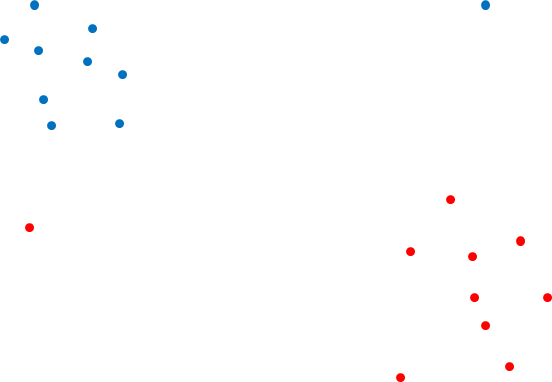
위의 그림에서는 decision bounary를 결정지을 support vector는 어떻게 결정지어야 할까?
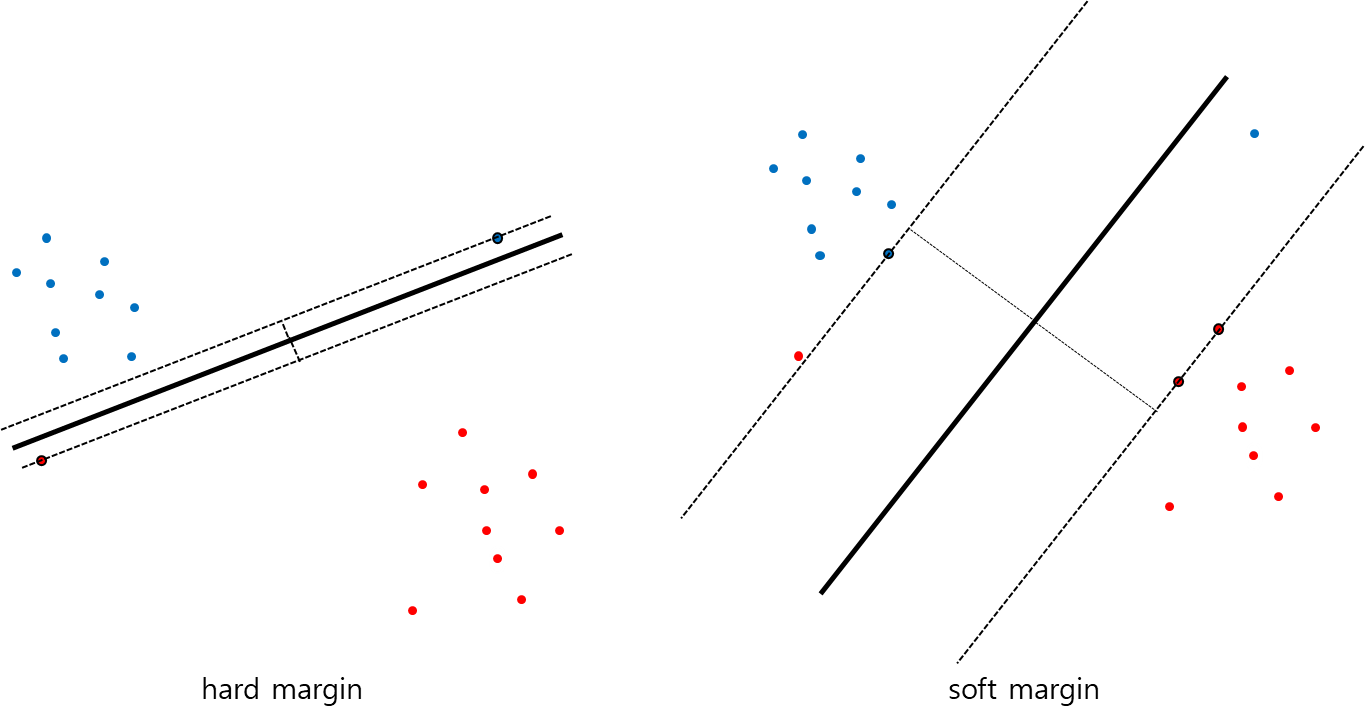
왼쪽 그림을 보면, outlier를 포함하여 SVM을 decision boundary를 결정하는 경우이다. 이것을 hard margin이라고 하며 margin이 매우 작으며, 모델이 주어진 학습 데이터에 오버 피팅 될 수 있다. 학습 데이터에 너무 완벽하게 학습되면 좋지 않다. 오버 피팅에 대해서 잘 모른다면 따로 공부하시길 바란다.
오른쪽 그림은 outlier를 포함하지 않고 decision boundary를 결정한 경우이다. 이것은 soft margin이라고 하며 margin이 이상적인 모양을 띄지만 학습이 잘되지 않아 모델이 언더 피팅 될 수 있다.
실제 코드로 구현할 때는 outlier를 얼마나 수용할 것인지 파라미터 등을 설정하여 SVM을 학습할 수 있다.
Kernel Trick
이번 SVM에 대한 설명은 Linear-SVM에 대한 내용이다. SVM은 선형적인 모델이므로 비선형적인 문제를 해결하기 위해선 다른 방법을 사용해야 한다. 이해를 위해 다음의 그림을 봐보자.
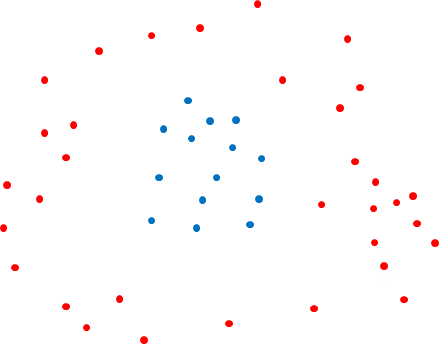
위와 같은 데이터의 분포라면 선형적인 모델로는 분류를 제대로 할 수 없을 것이다. 위의 데이터의 분포에서 SVM을 학습하기 위해선 Kernel Trick이란 방법을 사용해야 한다. Kernel Trick의 내용은 자세하게 설명하면 매우 길어지므로 마지막에 링크를 첨부하겠다. (다른 포스트에서 내용을 다루겠다)
Reference
study ref : https://towardsdatascience.com/the-kernel-trick-c98cdbcaeb3f
지적할 부분이 있다면 댓글 남겨 주시면 감사하겠습니다.
